Оглавление:





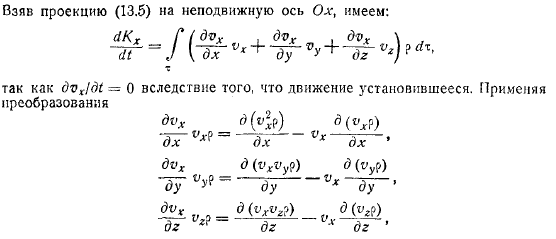





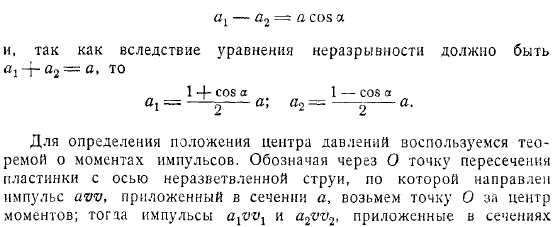
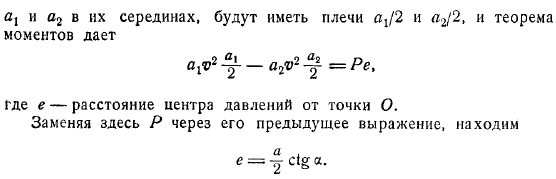

Применение закона количеств движения и закона моментов количеств движения
Эти законы установлены для системы материальных точек, между которыми существует внутренняя сила взаимодействия, равная попарно и противоположная, так что главные моменты и главные моменты внутреннего вектора равны нулю в каждый момент времени. В частности, оба закона гидромеханики применимы как к идеальному, так и к вязкому в случае стационарного движения жидкости закон импульса и закон моментов допускают простую геометрическую. To установите это, ограничьте себя идеальной жидкостью для упрощения и начните с особого случая для большей ясности.
Чтобы поток в целом или в последнем случае пилотирование крыла следует осуществлять в непосредственной близости от корпуса с жидкостной стороны.
Например, предположим, что за прандтлем следует струя несжимаемой жидкости, ударяющаяся о плоскую пластину под углом. Горизонтальная плоская струя начального и граничного условия, текущая от бесконечного к прямому с одинаковой скоростью во всех точках поперечного сечения ширины a, сталкивается с бесконечной пластиной под углом, и по мере удаления от точки ветвления она разветвляется на струи, асимптотически параллельные пластине; этих струй на бесконечности. Заметим, что скорость струи в сечениях совпадает со скоростью струи без ветвей (бесконечность). Фактически, если принять текущую плоскость за плоскость, то первые уравнения принимают вид.
В этом случае движение считается устойчивым, отсутствует массовая сила, и она равна. Вдоль той же линии потока умножьте эти уравнения, и суммируя, можно легко найти Интеграл (Бернулли). Допустимо для конкретной линии потока. Предполагая уравнение энергии, что давление свободной поверхности струи везде одинаково и равно атмосферному давлению, мы приходим к выводу, что скорость частиц свободной поверхности струи везде одинакова, поскольку в сечении скорость всех частиц равна.
Все частицы в сечении будут иметь одинаковую скорость. To рассчитав давление пластины, возьмем контур пилотируемой поверхности крыла, который обозначен пунктирной линией на рисунке. Это позволит ему примыкать к пластине между хорошо разделенными участками и пересекаться со струей, которая не разветвляется на достаточном расстоянии. Точно удаленное сечение сама поверхность может быть представлена в виде полной поверхности цилиндра блока, упомянутый выше контур в плоскости течения выступает в качестве основания и генератора, который перпендикулярен плоскости течения.
Форма контура области между сечениями остается произвольной. И для этого можно, например, взять свободную границу струи. А упомянутое выше давление на той части поверхности, которая не прилегает к пластине, является постоянным. Переменное давление части, прилегающей к пластине, может быть представлено следующим образом. При интегрировании с замкнутой поверхностью. Параллельная электрическая система.
Или то же самое суммируется на силу. Он применяется в определенной точке называемой центром теорема импульса. Когда запроектировано параллельное и перпендикулярное направление плиты. И по уравнению неразрывности, потому что оно должно быть. Чтобы определить местоположение центра давления, используйте теорему импульса. Когда импульс, приложенный в разделе, обозначается, точка принимается за центр момента. Импульсы затем применяются в поперечном сечении.
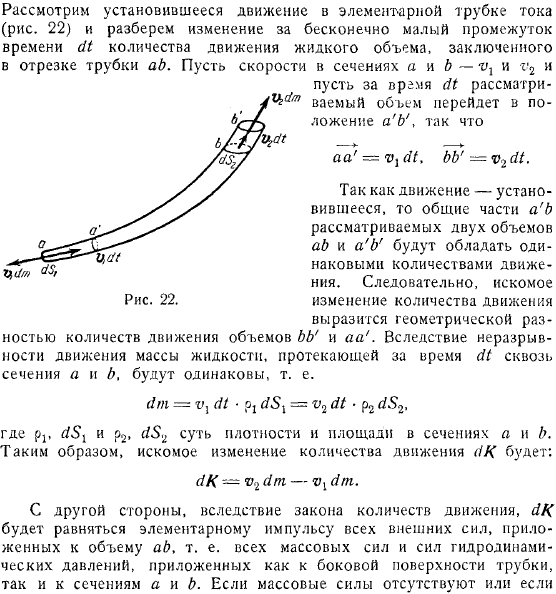
Плечо в средней точке — это момент, когда теорема дает. Если вы замените здесь в предыдущем выражении. Рассматривая основное текущее установившееся движение трубки, проанализируем изменение в минутном интервале времени импульса объема жидкости, заключенного в сегменте трубки. Разделы, а также изменение громкости на рассмотрении в положение. Второзаконие.
Поскольку движение является стабильным, общая часть из томов, рассматриваемых, будет иметь одинаковое количество движения. Поэтому желательно цифру. Изменение импульса. Он представлен геометрической разницей в объеме. Непрерывность движения массы жидкости, протекающей во времени сечений будет одинаковой.
Где плотность и площадь сечений, желаемое изменение импульса выглядит так. С другой стороны, по закону импульса равен всем внешним силам, приложенным к объему, то есть всем массовым силам, приложенным как к стороне трубы, так и к сечению, а также к основе импульса и гидродинамическим силам. Если нет массовой силы, или ими можно пренебречь по сравнению с давлением. И с представляющим основной вектор последнего.
Точно так же, применяя закон момента импульсов, повторяя предыдущий аргумент, он становится отношением. Где угловой момент объема жидкости радиус-вектор сечений основной момент гидростатического давления, приложенного к замкнутой поверхности объема.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Людмила Фирмаль
Равенства могут быть объединены с помощью одной формулировки, известной как теорема Эйлера. Если нет массовой силы, то совокупность гидродинамических давлений, приложенных ко всей поверхности определенного отрезка токовой трубы, соответствует силам в случае стационарного движения. Второзаконие. Приложенный к концу отрезка, он численно равен объему движения жидкости, которая вытекает и перетекает в трубку через участок конца.
Когда эти силы пересекаются, к твердому телу прикладывается набор гидродинамических давлений. Теперь мы применяем закон импульса и закон моментов к соединяющему объему конечномерной жидкости. Например, предположим, что неподвижная замкнутая поверхность нарисована в потоке жидкости, который обтекает неподвижное твердое тело.
Объем жидкости, заключенный в, имеет свою внешнюю граничную поверхность, а внутренней границей является поверхность твердого тела. Через бесконечно короткое время объем жидкости перемещается в положение. Это можно получить, отложив вектор от каждого элемента поверхности. В случае стабильного потока жидкости число перемещений общей части объема, заключенного в, практически одинаково.
Кроме того, изменение импульса объема жидкости во времени представлено геометрической разницей. Она равна границе объема жидкости, то есть основному импульсу всех гидродинамических давлений, оказываемых на поверхности и по закону импульса при отсутствии массовых сил. Где основные векторы давления, приложенные к. Точно так же, применяя закон момента момента момента момента, вы будете равны.
Уравнения представляют, что набор поверхностных гидродинамических давлений равен набору векторов, приложенных к поверхности элементов, равным движению числа жидкостей, протекающих через этот поверхностный элемент, и направлены вниз по течению. Этот результат может быть получен и чисто аналитическим путем. Учитывая установившееся движение жидкости, которое может игнорировать массовую силу, необходимо применить закон движения и момент движения числа к объему, заключенному между неподвижной (так называемой управляющей) поверхностью и «поверхностью твердого тела».
При нахождении суммарных производных знак производной можно отнести к векторам, так как они отслеживают частицы объема по мере их движения, а масса частицы не изменяется. Когда я получаю проекцию на фиксированную ось, она выглядит так. Это связано с тем, что движение является стабильным. Применение преобразований. Второзаконие. Интеграл теряется уравнением неразрывности. Для стационарных уравнений вид.
Если мы разделим первый Интеграл на члена и применим гауссовское преобразование к каждому из них, мы увидим, что. Второзаконие. Аналогично, мы получаем других равенства. Может быть объединен с вектором вместе с первым. Примените аналогичный вывод к следующему выражению производной момента. Поскольку — это масса жидкости за единицу времени, проходящая через поверхностный элемент, уравнения указывают, что считаются основными моментами основного вектора и вектора системы.
Нет. Совокупность поверхностных сил гидродинамического давления, оказываемого на поверхность объема при установившемся движении, соответствует совокупности движений жидкости, совершаемых ежесекундно через поверхность. Такая интерпретация закона импульса и закона моментов может помочь рассчитать общий эффект установившегося давления на погруженное неподвижное тело.
Из законов Ньютона можно показать, что при движении системы в пустом пространстве импульс сохраняется во времени, а при наличии внешнего воздействия скорость изменения импульса определяется суммой приложенных сил. Людмила Фирмаль

