Оглавление:











Функции нескольких переменных
- Функции некоторых переменных /. Функции двух переменных и их область действия До сих пор мы рассматривали функции, которые зависят от одной переменной. В этой главе описываются функции, которые зависят от некоторых переменных. Давайте посмотрим на некоторые примеры. Пример 1. Площадь S прямоугольника зависит от двух величин: основания x и высоты y. Эта зависимость выражается как: S = xy. (1) Каждое положительное значение * и пара y) из уравнения (1) соответствуют конкретному значению области 5. Считается, что площадь S прямоугольника является функцией основания x и высоты y.
Пример 2. Сила тока / но зависит от закона Ома для двух величин: напряжения U и сопротивления R. , /? </? </? (3) (Uv R1 и R2 являются постоянными), каждая пара значений U и R, которые удовлетворяют неравенству (3) согласно уравнению (2), соответствует конкретному значению текущей интенсивности /, то есть / Функция R. Следующие определения обобщают эти примеры: Переменная определения z называется функцией двух переменных x и yy в следующих случаях: 1) Задано множество G пар чисел x и y. 2) Дано правило, что каждая пара (x, y) чисел в этом наборе соответствует уникальному числу в r.
Предполагая, что U и R изменяются в пределах определенной конечной границы в эксперименте Людмила Фирмаль
В этом случае переменные x и y называются аргументами или независимыми перем2) Дается закон, где каждая тройка (x; y, r) чисел в этом наборе соответствует уникальному значению. Переменные x, y и z называются аргументами функции или независимыми переменными. Множество Q, образованное всеми тройками (x \ y \ z) числовых значений аргументов x, y и z, называется областью определения или областью функций трех переменных. Функция с тремя переменными указывается так же, как и функция с одной или двумя переменными. «= * / (*» U. z), w = w (x, y, r) и т. Д. Функцию трех переменных u — f (x, y, z) можно рассматривать как функцию точки P (x, y, z) с координатами x, y, z в пространственной системе координат Oxyz. Используя геометрические термины, аналогичные принятым для функции двух переменных, мы говорим, что область функции u = / (x: y, z) представляет собой набор конкретных точек в пространстве.
Метод определения функции для трех переменных u = f (x, y, z) может сильно различаться, но наиболее важным в этом курсе является определение функции с использованием аналитического выражения Это определить метод анализа. Кроме того, во многих случаях область определения функции не показана. В последнем случае область определения функции (область определения) рассматривается как множество всех точек P (x \ y \ z) в пространстве, где это выражение имеет смысл и дает фактическое значение функции u , Пример 1. Поиск области действия функции m = Y \ —xr — y * —r *. Решения. Это выражение дает фактическое значение, только если: 1 — x2 — y2— илиенными. Определение функции с двумя переменными аналогично указанию функции с одной переменной.
| Несобственные интегралы | Предел функции нескольких переменных» непрерывность функции. Точки разрыва |
| Приближенные методы вычисления определенных интегралов | Частные производные |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Мы подробно рассмотрели понятие функции двух переменных и их области определения. Однако на самом деле есть функции, которые зависят от более чем двух переменных. Например, объем V кубоида зависит от трех измерений: длины a и ширины b его основания и высоты h параллелепипеда. V = абх. Вот определение функции с тремя переменными: Определение В следующем случае переменная называется функцией трех переменных x, y и r. 1) Дано множество Q троек из чисел x, y и r.
Точки на граничной сфере принадлежат области определения функции. Аналогично, понятие функций 4 и 5 может быть введено: Обычно n переменных. Определение В следующих случаях переменная называется функцией от n переменных x, y, r. 1) Дан набор систем чисел X * Y * 2 (x, y, z, …, t). 2) Каждая система в этом наборе (x, y, r, /) имеет закон, соответствующий уникальному значению и.
Таким образом, областью определения функции является шар с единичным радиусом с центром в начале координат. Людмила Фирмаль
Например, u = x2 + 3y + 2r2-t8 является функцией четырех переменных x, y, z и / и определяется для любого значения этих переменных. Нотация функции для n переменных аналогична нотации функции для двух и трех переменных. «= / (*, Y, .t) и т. Д. Чтобы сохранить полезные геометрические термины, функция η переменной u = f (x, y> z, /) с η> 3 является точкой P (x \ y \ r \ () и — J (P). Точка P (x \ y \ r \ …; /) в таком случае означает систему из n чисел (x; y, r; …; t). Числа x, yt z, .t называются координатами точки P (x \ y \ z; …; t). Множество всех точек P (x; y; r; ./) с n координатами называется n-мерным пространством.
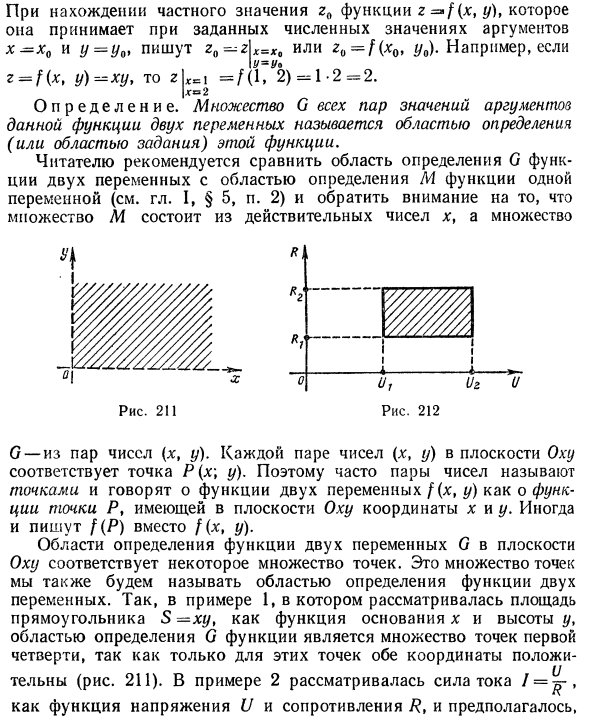
* * = / (*, Y) t 2 = 9 (A ‘, y)> z = z (x, y) и т. Д. Аргумент x — Нахождение конкретного значения r0 требуемой функции z = »f (x, y) для определенного числа x0 и y = y0, r # —r | *« * in или r0 = f ( * 0, у0). Например, z = f (xt y) — x>, то zL, = f (0) = 1-2 = 2. | dgo2 Определение Множество G всех пар значений аргументов для данной функции двух переменных называется областью определения (или областью задач) этой функции.
Читатель сравнивает область G функции двух переменных с областью M функции одной переменной (см. Гл. I, § 5, стр. 2), а множество M состоит из действительных чисел x и множеств Обратите внимание, что море -1 1 1. .. или Рисунок 212 Рисунок 211 and2 да Из пар G-номеров (x, y). Каждая пара чисел (x, y) в плоскости Oxu соответствует точке P (x \ y). Таким образом, во многих случаях пара чисел называется точкой и представляет собой функцию двух переменных f (x, y) как функции точки P с координатами x и y в плоскости Окси. Иногда мы пишем f (P) вместо f (x, y).
Область определения функции двух переменных G в плоскости Оху соответствует определенному набору точек. Этот набор точек также называется областью определения функции двух переменных. Таким образом, в примере 1, где площадь прямоугольника S_xu считалась функцией от основания x и высоты y, только эти координаты положительны, поэтому область G функции — это набор точек для первой четверти (рис. 211). , В примере 2 сила тока / = рассматривается как функция напряжения U и сопротивления R,
В зависимости от условий эксперимента Ux <I) ^ 0r, ^ R Rt. Область определения функции G здесь представляет собой прямоугольник, окруженный линиями U = Ult U = Utt R = и R-R2 (рис. 212). Координаты U и R этой прямоугольной точки (включая границу) удовлетворяют неравенству (3). Напротив, координаты точек вне указанного прямоугольника не удовлетворяют неравенству (3), поэтому эти точки не входят в область определения функции. Как и в случае функций с одной переменной, способ определения функций для двух переменных может сильно различаться.
Функции могут быть настроены с использованием таблиц (табличный способ настройки функций). Для функции z = f (x, y) такая таблица (таблица с двойными записями) имеет следующую форму, например: X 0 1 2 3 4 0100 81 63 45 28 1100 83 65 48 32 2 100 84 68 51 35 3100 84 69 54 39 4 100 85 70 56 42 Ячейка в левом столбце этой таблицы показывает значение аргумента xy в ячейке верхней строки, то есть значение аргумента y. В остальных ячейках таблицы указано значение функции r.
Кроме того, когда значение x выбрано в ячейке в первой строке, а значение y выбрано в ячейке в столбце fe-ro, соответствующее значение z является строкой / столбцом i. Например, если x> 3 и y-2, z = 69. Следующая таблица соответствует температуре x (градусы Цельсия) сушильного термометра и относительной влажности z (в процентах) в зависимости от разницы температур между сушильным термометром и влажным термометром. Наиболее важной частью этого курса является метод анализа, который использует аналитические формулы, чтобы указать, когда функция определена (используя формулы).
В приведенных выше примерах 1 и 2 функция была установлена аналитически, область задания первого примера была определена из геометрических соображений, а второй пример был определен из условий эксперимента. Однако во многих случаях функция двух переменных задается только с помощью формулы и не указывает область определения. Ложь и функции двух переменных определяются с помощью аналитических формул без дополнительных условий, область их определения такова, что на плоскости Окси эта формула имеет значение и дает фактическое значение функции Рассматривается набор баллов
Например, многочлен первого порядка r = ax + by-fc, многочлен второго порядка r = ax * + bxy + cy * + dx + ey — \ — f и т. Д. — все пары чисел (x, y) То есть весь самолет Ванфу. Рациональная функция двух переменных, то есть отношение двух полиномов к x и y, задается знаменателем Она исчезнет. Следовательно, рациональная функция r = ** z * / Делится на всю плоскость Oxu. Однако прямая x — y = 0 исключена. Вот еще один пример для нахождения области определения функции. Пример 3. Найти область определения функции r = ln (1 —x2-y2).
Решения. Функции определяются только с помощью выражений. Доменом этой функции является множество всех точек, для которых определено выражение In (1 — x2 — y2), то есть множество точек, где 1 — x2 — y2> 0 или x2-if <1. Поскольку формула x2 + y2 является квадратом расстояния точки P (x \ y) от начала координат, только точка с расстоянием от начала координат Координаты менее 1. Многие из этих точек образуют внутреннюю часть круга с центром в начале координат и радиусом 1.
Пример 4. Найти область функции z-arcsin (** — | -j / 2-3). Решения. Функция предоставляется и определяется -1 + -3 <1, Это эквивалентно условию Граница области определения представляет собой круг x2 — \ — y1 = 2 и x2 — \ — y2 = 4 Это также относится к этой области. Таким образом, область определения функции состоит из точек между окружностями x * + y * = 2 и + = 4 и точек на этих окружностях (рис. 213). 2. График функций двух переменных График функции от одной переменной y до f (x) в декартовой декартовой системе координат на плоскости обычно является кривой. График функции двух переменных z = f (x, y) в декартовой декартовой системе координат в пространстве обычно является поверхностью.
Фактически функция z = f (x, y) определена в области O (рисунок 214). Каждая точка P (x \ y) в этой области соответствует определенному значению функции z- / (P). Используйте это значение z для точек M приложений с системой координат Ohug. Эта точка имеет ту же абсциссу и ординату, что и точка P (таким образом, точка P является проекцией точки M (x \ y \ r) на плоскость Ohu). Затем каждая точка P в области G соответствует отдельной точке M в пространстве.
Вся область соответствует определенному набору точек М и обычно образует поверхность. Эта поверхность называется графиком функции z = f (x, y). Если поверхность представляет собой график функции двух переменных, уравнение, которое определяет эту функцию, называется соответствующим уравнением поверхности. Аналитическая геометрия уже учитывает несколько поверхностей, которые являются графиками функции двух переменных.
Помните некоторые из них. х1 и * Эллиптический параболоид есть функция z = (P и q — константы с одним и тем же знаком) (см. Рис. 100). Гиперболический параболоид является графом функций. z = yp — Yq (P и H — постоянные с одним и тем же знаком) (см. рис. 101). I) •> 2 Вершина эллипсоида ++ — 1 (см. Рисунок 96) является графиком функции _ И ниже это график функции 3. Функции трех и более переменных

