Оглавление:

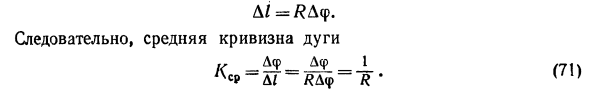


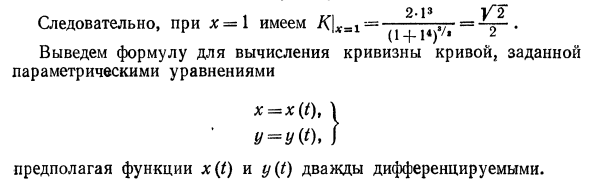



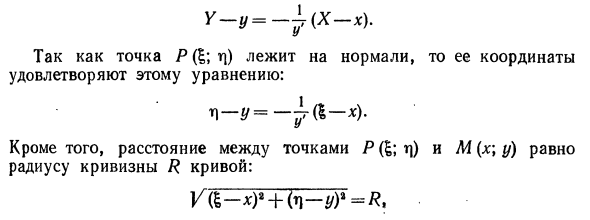

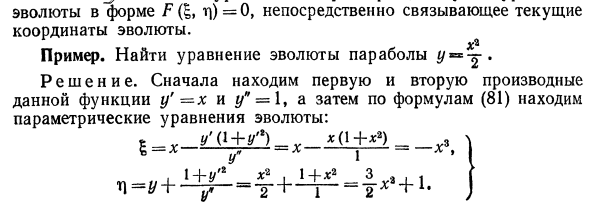



Кривизна плоской кривой
- Кривая плоской кривой /. Определение ключа При перемещении из одной точки в другую (которая совпадает с прямой линией) касательная призмы не меняет направление, но при перемещении из одной точки в другую вдоль кривой касательная вращается под определенным углом. вы. «Кривизна» кривой. В этом основное отличие прямых и кривых. Затем сравните две разные кривые (рисунок 197). Интуитивно очевидно, что кривая / изогнута больше, чем кривая II. Однако, чтобы точно оценить кривизну конкретной кривой, кривизна должна быть точно определена математически. Давайте дадим кривую.
рис. 198). Нарисуйте касательную в точках M и M. При перемещении из точки M в точку Mx вдоль кривой касательная вращается на угол Df. Это называется смежным углом. Я думаю, что этот угол является положительным. Средняя кривизна определения дуги ММ называется. Отношение смежного угла Df к длине D / этой дуги: D / Cav = ^ g. Пример. Найдите круг со средней кривизной и радиусом R дуги окружности MM (рис. 199). Решения. Угол Df между касательными окружности в точках M и Mlf явно равен центральному углу Df между радиусами OM и OMT. Длина дуги мм иен
На этой кривой рассмотрим дугу AfAft длины D / ( Людмила Фирмаль
Поскольку точка P (5; r]) находится на нормали, ее координаты удовлетворяют следующему уравнению: L — y = -x). Кроме того, расстояние между точками P (t; r ) и M (x \ y) равно радиусу кривизны R кривой. (N • } «2 n — 0. Затем кривая вогнута, и вам нужно использовать знак плюс справа от> y (см. Рис. 202), то есть выражение r (80). Часть выражения £ является знаком минус. Кроме того, поскольку y «> 0, \ y» \ = y «, получается следующее выражение для координат g и m] центра кривизны. (81)
Если y <0, мы видим, что уравнение (81) сохраняет свою форму. 4. Эволюция и эвольвента Если точка M движется вдоль определенной кривой, то, вообще говоря, соответствующий центр кривизны P также представляет определенную кривую. Определение Геометрическое положение центра кривизны конкретной кривой называется ее вырождением. Сама кривая эволюции называется эволютой или разворотом. Если уравнение кривой известно, уравнение (81) может выражать координаты центра кривизны ^ и r] в соответствии с абсциссой x. Другими словами, вы можете получить вырожденные параметрические уравнения. Исключение параметра x из этих уравнений дает уравнение / G
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Редукция вида F (s, «n) = 0. Это напрямую связывает текущие координаты редукции. Пример. • Найти параболическое уравнение вырождения Wa ~ 2 Решения. Сначала найдите первую и вторую производные y ‘—x и y «= 1 этой функции, затем используйте уравнение (81), чтобы найти вырожденное параметрическое уравнение.
Откуда Получено эволюционное уравнение, которое напрямую связано с текущими координатами. Вырожденная парабола y = ^ была полукубической параболой. На рисунке 203 показана парабола * / = -! => — И его эволюция. 2 улитки EVmbesoa Он указывает на две важные характеристики эволют и эволют (без заключения).
Таким образом, форма параметрического уравнения Evolute имеет вид Если мы удалим параметр x из этих уравнений, мы можем получить его непрерывно следующим образом: N R2 Рис. 203 = f ИЛИ | или s (t1_1) 3 = A Людмила Фирмаль
Нормаль эволюты — это тангенс эволюты в соответствующей точке (рис. 204). 2. Если радиус кривизны изменяется лютонно в конкретном сечении эвольвенты, то приращение радиуса кривизны этого сечения равно длине дуги соответствующего сечения и абсолютному значению Развиваясь. Например, рисунок 204 PXP2 = R2 — Rx \ PzPd = R9— Показывает, как использовать эти свойства для построения эвольвенты и изучения ее эволюции. Далее предположим, что у эволюции нет точек перегиба. Натягивайте нерасширяемую гибкую пряжу на РХРА Evolute. Имеет свободную прямую часть РХМХ (не растянутую на эволюте).
Поместите карандаш в точку М. Теперь разверните нить и держите ее натянутой. Карандаш рисует линию, которая является эвольвентой указанного эволюта PXPV. Очевидно, что в зависимости от длины свободного сечения нити PXMX вы можете получить бесконечное число различных эвольвент этого эволюта.
D / = NDf. Следовательно, средняя кривизна дуги Для Au_ Af_ / ХсР «~ Д / ЯДф Таким образом, средняя кривизна дуги конкретного круга является постоянной величиной и обратной величиной ее радиуса. Тем не менее, в целом, средняя кривизна не может быть одинаковой в разных частях кривой. Чтобы охарактеризовать кривизну линии вблизи заданной точки, необходимо взять среднюю кривизну все меньшего сечения дуги, содержащей эту точку.
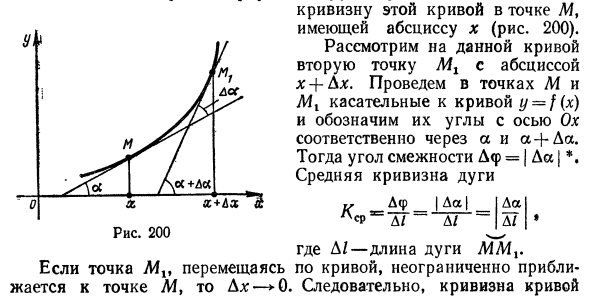
Таким образом, мы становимся понятием кривой кривизны в данной точке природы. Кривизна кривой в определенной точке M является пределом средней кривизны дуги MMg, при условии, что кривая бесконечно приближается к точке M вдоль этой кривой. К-нш / сср. (72) В частности, кривизна окружности радиуса R в точке М / С = »Шп / Сср = Нш- = 4-. Таким образом, в любой точке окружности кривизна имеет одинаковое значение, равное обратной величине радиуса. (73) Предоставьте читателю возможность доказать, что кривизна линии в любой точке равна нулю. 2. Расчет кривизны. Кривая задается уравнением y = f (x). Функция f (x) может быть дифференцирована второго порядка в интервале (a, 6). То есть каждая точка в интервале имеет первую и вторую производную.
Рассчитать Кривизна этой кривой в точке М с абсциссой х (рис. 200). Рис. 200 Учитывая эту кривую, рассмотрим вторую точку Mx с абсциссой x + kx. Нарисуйте касательную в точках M и Mx с помощью // // f (*) и укажите угол с осью Ox с помощью a и a + yes соответственно. Далее смежный угол D
0, если точка Mlt движется вдоль кривой и бесконечно приближается к точке M. В результате кривизна кривой
В то время Да д / Лира к L1X м ободок д * -о брак Разделение числителя и знаменателя на Dx дает: ,. Я да лим-д * -о я л * да дх Это верно L * dl_ дх V я ЮЩИЕ О д * -и л * К = * НШ О — о A = arctg y ‘(если y’> 0) или a = n + arctg y ‘(если y’ <0), в зависимости от геометрического значения производной y ‘- \ ga. Оба случая (Y ‘) * Кроме того, ^ = (см. Уравнение (54)). Замените эти Выражения ^ и в уравнении (74) имеют вид Da 1/1 / C = Ки-ф-й » (L + yrt) V » Поэтому для расчета кривизны кривой получается следующая формула: \ y «\ (1 + y’g) л / г (75) К = Пример 1c. Нахождение кривизны гиперболы y = в точке на абсциссе. к х = 1 1 * 2 Решения. у ‘= — ^, у «= 1 2 1 x3 | 21 * 1 » к v7- (1 + x4) (L + | r>
2-13 1 ^ 2 Таким образом, если x = 1, / <! , — = — j— = -. (1 -f-1) * Выведите уравнение для расчета кривизны кривой, заданной параметрическим уравнением х = х (т), \ у-мы). Я Предположим, что функции x (t) и y (t) дифференцируемы второго порядка. Тогда (см. Главу VI, § 4, с.2, уравнения (78) и (79). 4 <к \ (чу \ (4) … d’2y \ dx) \ dxjt \ xt / t = {* <) = ytxt — ytxt I * 2 dx xt x’t xi (x’tY ‘ Подставляя выражения y’x и y «x в выражение (75), W-1 yt x’t -y’l x «t 1,7 Пример 2. Циклоидная кривизна x = a (t-sin O »Y ~ -a (1-cos /). Решения. Мы находим последовательно: x \ = a (1-cost), y \ — = as \ nt, X / = sinyl-acost. Подставляя эти уравнения в уравнение (76), jr | a cos та (1 — cos Q — грех та sin t | | cos / -1 1 __1 [a2 (1-cosOa + aasin4] v «~~ a [2 (1-cos t)] ‘/ 9-4a • 1 Грех ~ 2 3.
Радиус кривизны. Круг кривизны. Центр кривизны Оказывается, что кривизна окружности является обратной величиной радиуса R. Чем больше радиус круга, тем меньше кривизна. По аналогии вводится понятие радиуса кривизны кривой в конкретной точке. Радиус кривизны R в конкретной точке на кривой определения является обратной величиной кривизны / C. R = X ‘(77) Как правило, радиус кривизны является переменной величиной, поскольку кривизна кривой изменяется при переходе от указанной точки к другой точке.
Если кривая задается уравнением y = f (x) t, радиус кривизны R в качестве обратной величины кривизны определяется как (78) Если кривая задана как параметрическая, ее радиус кривизны определяется как (79) \ yt Xt — yt XI I Пример. Найти радиус кривизны кривой y- \ nx в точке M (1; 0). Решения. Найти у ‘= -и у «= — . да (1 + * 8) ‘7 ”1 * 1 = 2 В 2. м х = \ Теперь построим отрезок MP в заданной точке M кривой, ориентированной перпендикулярно вогнутой поверхности кривой, равной радиусу кривизны кривой в точке M. MP = R = -l (Рисунок 201). Радиус, равный радиусу с центром в точке P Радиус кривизны кривой в данной точке = называется кругом Кривизна. Центр P этого круга называется центром кривизны.
Ясно, что эта кривая и круг кривизны точки M имеют общую касательную (рис. 201). Рисунок 201 Показано, как найти координаты центра кривизны кривой, заданной уравнением y = f (x). Пусть M (x \ y) — точка данной кривой, а P (|; m ^) — соответствующий центр кривизны (рис. 202). Форма нормального уравнения кривой в точке M (x \ y) имеет вид

