Оглавление:







Задачи, приводящие к определенному интегралу
- Задачи, которые ведут к конкретной интеграции /. Региональные проблемы В базовой геометрии учитывался участок плоской фигуры, окруженный отрезками прямых линий, а также участок круга и его частей. В связи с этим возникает проблема расчета площади вида K сверху, окруженного любой замкнутой линией (рис. 170).
(Рисунок 171). Эта фигура называется трапецией линии ползучести, а сегмент CD является ее очагом ——— ™ ————— Рис. 170 Рис. 171 Точки C и D имеют абсциссы a и b соответственно (6> a), а кривая AB для выбранной системы координат задается уравнением y = f (x). Где f (x) — это отрезок [a, b \ function. Разделите сегмент [a, b] на части, используя n — точки разделения с абсциссами. Хх <<. , , <* / <… <X, Кроме того, поместите a = x0 и b = x для однородности записи. Точка разделения разделяет сегмент [a, b] на n меньших сегментов.
Сначала рассмотрим особый случай, когда фигура K находится в плоскости Oxy и окружена кривой AB, горизонтальным сегментом CD и двумя прямыми линиями CA и DB, проведенными в конце сегмента, параллельном оси Oy. Людмила Фирмаль
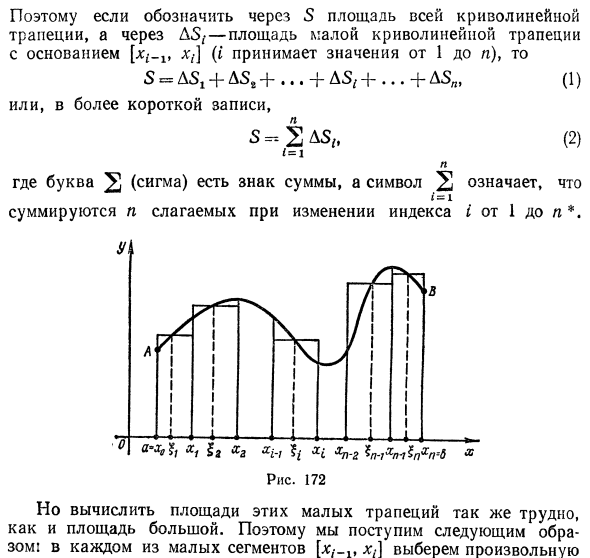
Нарисуйте прямую линию, параллельную оси Oy, через точку деления и разделите изогнутую трапецию на n небольших изогнутых трапеций (рис. 172). Очевидно, что площадь всей трапеции кривой равна сумме площадей всех трапеций кривой hmal / x. Поэтому, если площадь всей изогнутой трапеции равна 5, и отображается область небольшой изогнутой трапеции с AS [xt-lt xt] внизу (i принимает значение от 1 до n), S = AS, + AS8 + … + AS, + … + A5Я, (1) Или для коротких записей, S «2 AS ,, (2) 1 = 1 N Где символ 2 (сигма) является знаком суммы, а символ 2 означает, что n терминов добавляются, когда индекс i изменяется с 1 на n *.
Однако вычислить площадь этих маленьких трапеций так же сложно, как и больших площадей. Поэтому действуйте следующим образом: Любой в каждом из маленьких сегментов Укажите на это и постройте Ордината кривой f (см. Фиг. 172 и 173). Теперь замените каждую из маленьких изогнутых трапеций основанием (/ = 1, 2, …, n), прямоугольником с таким же основанием и высотой / (5 /) (см. Рис. 173) , Площадь этого прямоугольника f (h) ~ x1 —x (-r — длина малого сегмента t * / -i »xi] на рис. 173 • занимает площадь этой линии Квадрат приблизительного значения небольшой изогнутой трапеции (3) AS «/ (?,) (*, -X, -t).
| Интегрирование некоторых иррациональных функций | Кривизна плоской кривой |
| Общие замечания о методах интегрирования. Интегралы, не берущиеся в элементарных функциях | Несобственные интегралы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Замена области каждой маленькой изогнутой трапеции прямоугольной областью, которая имеет такое же основание, но имеет высоту, равную ординате кривой в любой точке основания, приводит к форме шага, показанной на рисунке. 172. Площадь этой фигуры лестницы дает приблизительное значение для площади изогнутой трапеции. Таким образом, для искривленной области трапеции S получается следующее приближенное уравнение! 5 «/ (*! — *) + F (1d) (* 2 + … + / (Y 1). Или короткая запись, (4) 2 Вт (* — * / -O- Показывает максимальную длину маленьких сегментов в K! B = Наивный. {(! — X0) \ (x2- (xn-xn-x)). С уменьшением X точность приближенного выражения (4) возрастает.
Вот так S-lim 2 / (E,) ( r- * / -i) — (5) O / = 1 Кроме того, если мы обозначим x {-— x ^ x = D *, уравнение (5) примет окончательный вид: 5 = Нш2ШД *,. (6) o / = 1 Рис. 174 Поэтому расчет площади Изогнутая трапеция привела к нахождению определенных суммовых пределов вида (6). Возвращаясь к задаче вычисления площади плоской области / C, окруженной любой замкнутой линией, отметим, что эта проблема может быть сведена к проблеме поиска изогнутой трапеции. Например, область рисунка 174 ограничена
Поэтому, если максимальная длина K небольшой трапеции имеет тенденцию быть нулевой, вполне естественно, что точное значение площади S изогнутой трапеции принимает ограничение на общую площадь ступенчатой формы. Людмила Фирмаль
Контур ApWA можно найти как разность площадей между изогнутой трапециевидной AlBlBmAAl и AfifinAA ^ 2. Спросил о работе различных сильных сторон Если материальная точка под действием силы F, величина и направление которой не изменяются, перемещается на расстояние / в направлении силы, сила работает равной произведению силы F и смещения /, как видно из динамики. E ^ F-l. (7) Рассмотрим случай, когда значение силы F изменяется, даже если сила F сохраняет определенное направление. Сделайте так, чтобы масса двигалась по прямой вдоль линии силового действия при этом силовом действии.
Поднять задачу расчета работы силы Ф. Прямая линия, по которой движется материальная точка, берется относительно оси Ox. Добавьте координаты a и b к началу и концу пути соответственно (a ЧZ / hi £ n6 = xn x Рис. 175 Существует определенное количество силы. Это функция абсциссы. F = f (x). Эта функция считается непрерывной. Разделите сегмент [a, b] между началом и концом пути на n меньших сегментов (Рисунок 175) [x0, xr] y [x ,, x2], …, [x / j, x, -], .. [xl-1, xn \ (где g = x0, b-xn) соответственно Равная длина: A *! = xt x0, A ^ = x2 Xj, …, Dx4 * -X’t X / — ••• »D Xn-Xn x„ |. Работа [a, b] для всего пути равна сумме работы для всех небольших участков пути. Через xt] -D £, работая в небольшом разделе, показывая желаемую работу через E 1 = 1
Однако, поскольку силы не являются постоянными, определить работу в небольшой области так же сложно, как определить целое. Тем не менее, сегмент сегмента [я, -! , Xf] достаточно мала, сила на каждом небольшом участке пути слегка меняется из-за предположения о непрерывности функции F -f (x). Для каждого маленького сегмента х выберите точку В каждом небольшом сегменте величина силы имеет постоянное значение, равное значению в точке g ^ Z7 / = / (£ /) При этом предположении силовая работа на отрезке пути [x ^ lt, ,] согласно уравнению (7) равна = / (£,.) X, -. Но на самом деле, с небольшим отрезком х {], сила Так как является константой, выражение / (ξ,) Axf дает только приближение работы в этом небольшом разделе. Поэтому сайт [ / -i. XI]
И все время [а, б] N E «2 / (5 /) Л *, -. (8) я = я Это приближенное уравнение является более точным, и чем меньше A, тем меньше. Поэтому, если максимальная длина X небольших смещений имеет тенденцию быть нулевой, естественно, чтобы общий предел (8) был точным значением работы. N E = lim 2 / (h) A *,. (9) L.- * o 1 = 1

