Оглавление:


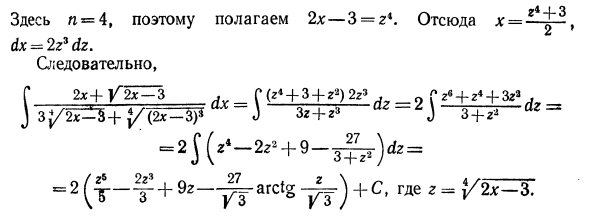



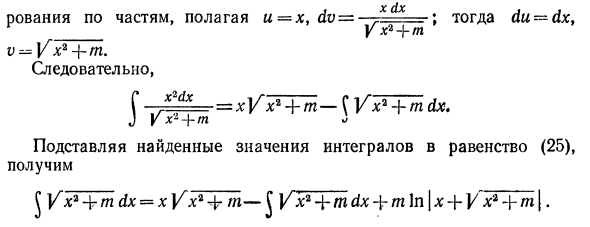

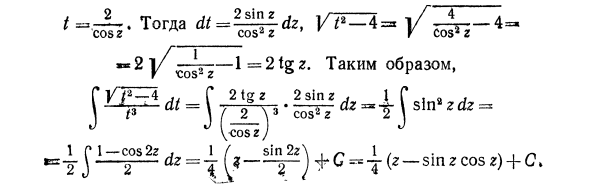

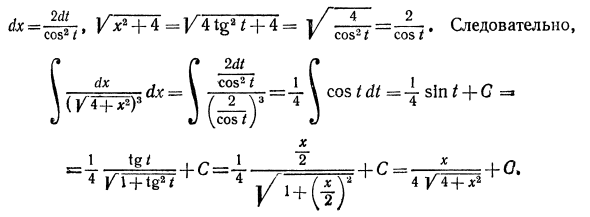
Интегрирование некоторых иррациональных функций
- Интеграция нескольких функций излучения Рассмотрим несколько типов интегралов, которые включают в себя [иррациональные выражения. /. Интегрирование вида J R (x; Уax + b) dx Показать интеграл J R (.x; y / ax + b) dx (23) Где n — целое число, R (x \ {/ ax-b) — рациональное выражение для x, а y / ax + b9 можно привести к интегралу от рациональной функции. На самом деле, интеграция выполняется (23)
t = -so cos z z = arccos «smz— cos z t 1 \ t J 1 =] / «l — cos2 z ■ =» Y l- = [arccosx + i- (FfT ^ J + c # Пример 2 <find j * Решения. Интеграл j * ^^ T x «dx — это тип I. η = 2 sin, dx = 2costdt, 4 — x2 = 4-4 sin21 = 4 cos21. = —Ct gt — t + c. T: ^ * ,, COS / -sin2 / Г ^ (т) Поскольку грех / = T, ctg / == — T ^ 2 = —-—, t = arcsin y. так J —— арксины y + C. интеграл л * Dx обсуждается в пункте 3 Он принадлежит к типу I и может быть вычислен путем замены x = на \ nt. Использовать дх Пример 3 Поиск <\ ,, •. -. J (/ 4-f * 2) 3 Решения. Это интеграл типа II. Установить х = 2тг
Таким образом Возвращаясь к переменной x (t = x — \ — 1) J 1) 3 4 Людмила Фирмаль
-II ‘+ + 4- F f * «^ = \ = 4. \ Cos tdt = 1 sin t + C (Cos /) (^ 4 + * ‘) / 2 4 \ 4 X 1 Джг ^ _ 1 1 2 = _ 4 л ^ л + тг «* 4 4/4 + * 2 Установите ax — \ — b-zn \, чтобы изменить переменную, x = 2b, dx = н-1 дз, вакс — \ — b = r но Друзьям Интеграл в правой части уравнения является интегралом рациональной функции по интегральной переменной z и поэтому может быть найден способом, описанным в §3. Пример 1. Найти Г * ~~ .. dx. V П) х-2 Решения. Где топор — \ — b = x и n = 2. Установите x = z2f. Вот дх-2з дз. немедленно J x-2 \ D X J 2 2z J 2-2 Поэтому мы свели интеграцию к рациональной интеграции функций. Если вы замените выражение через x вместо z, то есть, используя z = yrxt, [—2 {Vrx + \ n \ Vi; -2 ) + C. J x — 2 уд: Пример 2, поиск Решения. Если мы приведем радикал к тому же индексу подынтегрального выражения, мы уверены, что он разумно зависит от U2x — 3 _ 2 * + (J / 2x-3) 2 пг
Где n = 4, поэтому установите 2x — 3 = r4. Следовательно, х = г <+3 дх = 2z * dz. так J J Zg + r »dz ~ 2 J s + *> dt = 2Kr-2r2 + 9-b) <, r = Более общая форма интеграции: W «Vga) *. Где рациональное выражение x и jf ™ сводится к рациональному интегралу функции перестановкой Jj = r 2. Интеграл вида 1 Mx + N ax. J U Ah * + Bx + C Конкретный тип этих интегралов являются интегралами G Ах G_cix_ J И J Y ^ TIG * Первый интеграл табличный: G-7rM = r = арксин- + C (VII G) J u a * -x * a Чтобы вычислить второй интеграл, измените переменную, возведя в квадрат обе стороны уравнения Vx2 — \ — m = -x + и получите x * + m = xr-2xt + t2. Отсюда t2 — m, t * + m A, х = ~ 2—> дх = — ^ — дт. Кроме того, Vx2 — [- m = -x + t = -T ~ ‘ Ст2 + м + C 2 / Но / = Vx2 + m + x, так что в конце f 77 = = 1 «I x + V # T ^ \ + c. (XIX) J у х * + т
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Этот интеграл является общим, поэтому вам нужно запомнить уравнение (XIX). Теперь перейдем к интеграции формы j с j. ^ ^ \ ^ in \ -c IN » Интеграция путем изменения переменной t = (Ax2 + Bx-C) D Dt + E теграрам вида J — == dt. Вычисление последнего интеграла с A> 0 является интегралом вида (XIX), а если A <0, это интеграл формы (VIII ‘). Пример 1. Найти Г- = -dx * F V J Vb-2x-x *
Решения. —2x — xr) n: = -1- /, dx — dt и 6-2x-x2 = 6-2 (-1-0 — (- 1-t) * = 7— J yr6-2x-x * J Y7- / 2 J \ Tl-t * J y7- -4 r-7J === — K7 ^ -4arcsin- ^ + C = J- / а7 = — / b -2x — x2 + 4arcsin + C. Пример 2. Нахождение Γ * dx Решения. Положите следующее: / = y (x2 -f-4n ‘-f 5)’ = x + 2. Тогда x-t-2 dx = dt, Jt2 + 4; e-f 5 = (* -2) 2 + 4 (/ -2) + 5 = / a +1. Например, рассмотрим второй интеграл p, f-fx2-fm, T * 2dx. Дх / ог ΓJj по формуле (XIX)? = \ N \ x + V’jF + m \ + C J V x * — \ — т G x2 дх Рассчитать интеграл J V xg + t
Таким образом, G x dx _ G (t-2) d (_ G t dt 2 G dt _ 2 In + + -f-C = K * a + 4x-f-5—21п + 2 + + 4л * — | -5 | -fС. Интеграл семян [Va2 — x2 dx и J 1L * a-b / и dx Людмила Фирмаль
Частичное соотношение, гипотеза и -x, du = -; du-dx, поэтому J \ G * + t J Подстановка найденного интегрального значения в уравнение (25) дает: ^ yx47mdx = xyx * — \ rm- ^ Vхг + mdx — \ — m \ n \ x — \ — Vх * + т .
Справа и слева от последнего соотношения находится искомый интеграл искVx2 + µdx. Двигаться влево C V’x * + mdx = ± (xUx2 + m + m \ n \ x + Y * r + m ) + C. J V a2 — x2dx = * ~ fa * —x * + a2arcsin + C 4. Интегрирование вида JR (q; Y Ax2 4-Bx + C) dxt Где R (x; VAx2 H-Bx + c) — рациональное выражение для x и VAx2 + Bx + C. 1 в Заменить / = + C) ‘ Редукция — это сумма или разность квадратов, а интеграл jj R (x \ Y Axx * f Bx-j-C) dx является одним из следующих интегралов, в зависимости от коэффициентов A, B и C. I. Dty IIVa? + t *) dt, III. J R (t \ YlS-a2) dt.
Эти интегралы обнаруживаются с использованием следующих перестановок: Интеграция типа I. t = атгц интеграла типа II; Для интеграции типа III. Пример 1. Найти jdx. Решения. Сначала замените интеграцией / = * a + 2x — 3) ‘= x + 1, * = »* -1, dx = dt *, затем x% + 2x — 3 = = (Т-1) 2 + 2 (/ -1) —3 = / 2-4. Таким образом, Интеграл в правой части последнего уравнения является интегралом типа III. Рассчитать т = -. dt = 2 — ^ — dz, 1/7 ^ = 4-1 / * -4 = * cos z M cos ^ z ‘r V COS2Z V ^ coi ^ z «» ^ = 2tz. Вот так 1Г1 — cos2z, 1 (sin 2z \ .n 1, с. J-2— \ 1 * —— sinzcosg) + C

