Оглавление:


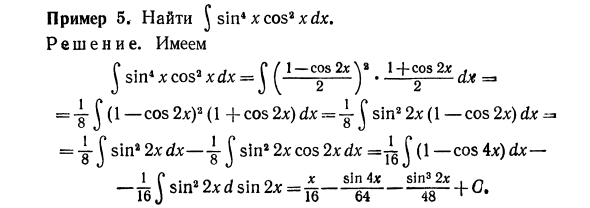



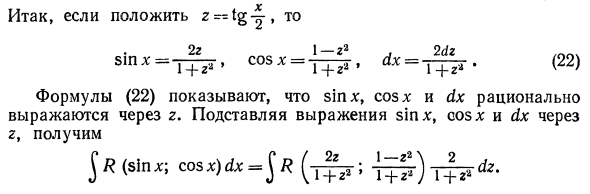

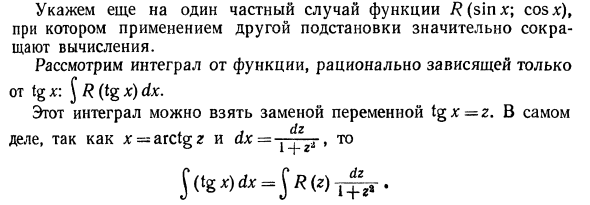

Интегрирование тригонометрических функций
- Интегрирование тригонометрических функций. Интеграл вида J sin «** cos ‘* xdx, где m и n — целые числа. Сначала рассмотрим случай, когда число m или n является нечетным числом. В этом случае интеграл сводится к интегралу рациональной функции. Суть метода интегрирования понятна из следующего примера. Пример 1. Найти J sin5 xcos4 xdx. Решения. Обратите внимание, что sin xdx = -d cosx, измените переменную, установив z = cos *, и go даст dz = –sin xdx, так что sin2x = 1 –cos2x = 1 — za , J sin5 x cos4 x dx-J sin4 x cos4 x- sin xdx = -J (1 -z2) 2z4dz = = -J (z4-2ze-fz «) dz = -4 + -7! —F + C = 3 -COS5 X, 2 COS7 X cos9 x, n-5 часов 7
Решения. Измените переменную, установив z-igx. Далее x = arctan z, dx = j d * z ,. так + * axctgz- ± \ n (\ + z ) + C = ± \ n \ tgx — \ — l \ + ± x— 1 + с = потому что х -iln (tg « + l) + C = -iln | tg * + l | + = in In | sin x + cos x | + y x + C. Пример 4. Jtg »* <k = j1 ^ = i ((z — rpp) <fc = 4-T, n (1 + z *) + -f в | cos x | + C Замечания. Если sin * и cos * встречаются только в четных степенях, одно и то же замещение является целым J /? (Sinx; Cosx) Возьми dx. Это вытекает из того факта, что sin2 * и cos2 * разумно представлены через tg *. sin2x =. 7 = cos2a: -1 1 4-ctg2 l: l-f-tg2 * ‘L 1 + tg2 d; # DZ PR-R Chn ^ Lt ^^ N ^ -T? * «* — ^ —
Последнее подынтегральное выражение является рациональной функцией от z. Idx тг ~ с + т ‘ Людмила Фирмаль
Пример 2: Поиск «J- ^ li-dy». Решения. cosxdx = ds \ nxt и установить z = sinx, dz = cos xdx, cosax = 1-sin2 x = 1 –2 *, sinax = 2a и = — z + C = -J-sin * + C г 1 грех х 1 Замечания. Тот же самый метод может быть применен, когда одно из чисел m или n является нечетным и положительным, а другое является действительным. Пример 3, поиск х грех * хдх. Решения. J j / cos2 x sin3xdx = J cos2 / 3 x sin2 * sin x dx. Поместите cosx-r и установите dz = — sinxdx. так J £ / cos2xsin3xdx = — ^ z2 / 3 C1-z2) dz = — $ (r2 / 3 —z9 ‘>) dz = * + C = 3cos * y ^ Flc + c.
Где показатели m и n оба являются неотрицательными четными числами (особенно один может быть равен нулю). Замените sinax, cos2 *, sinхcosх в формуле , 2 1 — cos 2 * «1-f-cos 2 . __ 1. N Sin2X = -2- ”COS X = -2-, sin xcosx = ySin Произведение sin /, x «cos’nx заменяется суммой произведений аналогичной формы, но индекс ниже. Метод интеграции понятен из следующего примера. Пример 4. Найти cos2xdx. Решения. У нас есть J COS « Ls = J = i + + s.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Пример 5. Найти J sin4 xcos2xdx. Решения. У нас есть Г- «i Loa lГ / 1-cos2x \» 1 -f cos 2 #. \ sin4 * cos2xdx = z \ [-2-) * — ~~ 2- = ^ j (1-cos2л 🙂 2 (1 + cos2х) d * = 4 «j sin * 2x (l-cos 2x) ** = 2 Когда sin2 2xdx-i-J sin2 2x cos 2xdx == — J (1 — cos 4x) dx — iG • 9оj • о * sin sin32л; -IS J sin »2xds.n2A; = 1g —— 48» + ° ‘
ЗамечанияЭту ситуацию необходимо учитывать (особенно при интеграции тригонометрических функций), поскольку ответы могут быть получены в разных форматах в зависимости от метода интеграции. Так, например, J sin 2xdx = -уcos 2 * + С. Но с другой стороны, J sin 2l: dx = J 2 sin a: cos xdx ~ 2 J sin Ardsinx = sln2x + C Так -ycos2x и sin2 * являются обратными производными
Как известно, примитивы из одной и той же функции отличаются друг от друга в зависимости от постоянного члена. Людмила Фирмаль
Для той же функции sin 2 * постоянные члены отличаются друг от друга для ясности. —Y cos 2l: = — y (cos2 x — sin2 l 🙂 = «- y (1-2 sin2 l 🙂 = — y + sin2 x. Для дальнейшего изучения того, как интегрировать тригонометрические функции, вам понадобятся новые концепции, описанные в следующем разделе. 2. Рациональные функции двух переменных Полином для двух переменных u и u является суммой произведений вида Ai, um. Где n и m неотрицательные целые числа. Например, выражение 3u * v 4-5i5u4-5u3 — {- 6, 5y2-f4w является полиномом относительно u и v.
Частное деления двух многочленов для и и v называется рациональной функцией для и и и и, или рациональным выражением для и и а. TI * wa + 3u 2 м2 –i2 3 Например, дроби и> ^ 4p1, — ^ -, ^ p ^ 3 являются рациональными выражениями для u и u. Рациональные функции от u и v представлены R (u \ v). Вы можете видеть, что сумма, разность, произведение и частное некоторых рациональных функций u и y также имеют рациональные функции a и c. Рациональные выражения для функций q> (x) и h}> (x)
Называется рациональной функцией от a и y, а φ (*) заменяется на и вместо —FM. *)). n 1 Yx + b — X Пример I, у— рациональное выражение для х и Vx + 4. грех х -4- cos3 х Пример 2, выражения gin3 x-f-2cos2x — Pa1 * и 0nal1n0e для sin * и cos *. Отметим, что если (p () и φ () — рациональные функции от *, (((()) также является рациональной функцией от *. 3. \ /? Интеграл (Sin x; cos x) dx В этом разделе мы рассмотрим общий способ поиска интегралов вида J R (грех *; cos *) дх, Где R (sin *; cos *) — рациональное выражение для sin * и cos *. Например, такой интеграл является интегралом дх Грех х ^ m3xcos’xdx ‘J
Наоборот, интеграл J sin7 / 4 * cos2 * d * не является интегралом этой формы. Потому что интеграция является неразумной функцией по отношению к греху * и cos *. Интеграл вида J R (sin *; cos *) dx указывает, что он может быть сведен к интегралу рациональной функции. Для этого вместо * введите новую переменную z, которая связана с переменной z отношением 2 = тг | • (21) Тогда грех * и cos * разумно выражаются через r. На самом деле, используя формулу, известную из тригонометрии, 0. X X 2sin | .cos | 2tg | 2g sin * = 2 sin -tgcos -77 = 2 2 cos * | + sin * i- l + tg2! * + Как хорошо COS2-Sin2 -77-1-tg2 — ^ -. » „X., x 2 2 b2 1 — g2 COS * = COS2 -75-Sin2 -75- = — = — = Т-Г-.Г. 2 2. , * •> 1 4-я * cos2 y + sin2-J l + tg2-g- Наконец, если z = tg y, мы находим * = 2 arctan zf dx = ^^.
Поэтому при размещении z ~ tgy, 2z 1_22 чат sinA ‘= TTir, cosx-y ^, (22) Уравнение (22) показывает, что sinx, cosx и dx разумно выражены через z. Подставьте выражения sinx, cos *, dx в r, чтобы получить jtf (sin *; cosx) dx = $ R (7 | ir; -L = £ l) Последний интеграл является рациональным интегралом функции переменной z и может быть вычислен с использованием метода, рассмотренного в §3. Jdx-. Грех х Решения. Если мы установим z = tgy и применим уравнение (22), 2 dz _ 1 + 2 » -В I y _ _ r-Ура. _ 2z I -f g- дх потому что х In | r | -f-C = In tgi. | + C Грех *
Пример 2. Поиск ^ Решения. Предполагая, что z-tg y, 2dz_ найдено н-тг | 7 1 J- ‘1 + 2 l + C = In дх 1 -f-z * = 2 + с 1 — z 1 г 1 + г * потому что х я * х «2 так — = В 1- g- = ln | tg (| + i) | + C = ln | tg || + C, (T + t) | + C » ( дх (XVIII) (XVIII) Грех х — В J дх потому что: Рекомендуется запомнить эти формулы. Перестановка z = tgy, но интеграл J (sin x; cos x) dx всегда Он сводится к рациональной интеграции функций, но его зачастую очень сложно вычислить. Поэтому часто рекомендуется использовать другие методы, чтобы найти этот интеграл. Так, например, если R (sinx, cosx) = sin «xcosw x (m и n — целые числа), более удобно использовать метод, описанный в подразделе 1.
Укажите еще один особый случай функции (sin dg; cosx). В этом случае использование другой замены может значительно сократить расчет. Рассмотрим интеграцию функций, которые зависят только от Из txx: ^ R (tg x) dx. Этот интеграл можно получить, изменив переменную tg x = z. в На самом деле, х является арктаном g и dx = t, поэтому J (TG = (G) RG

