Оглавление:







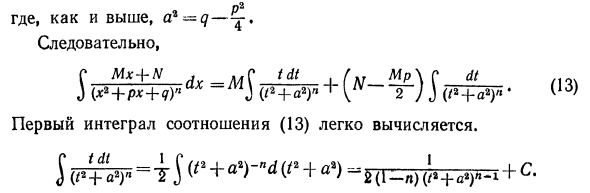

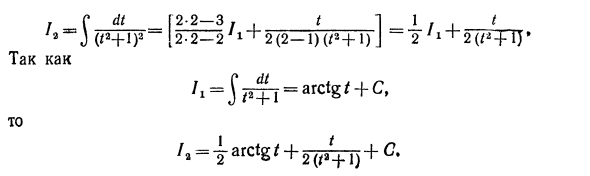


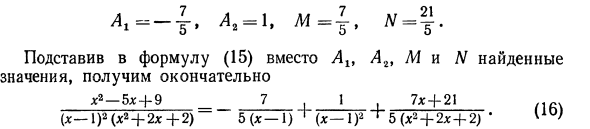



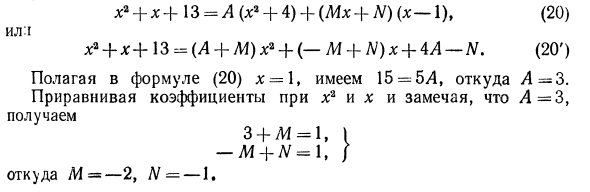
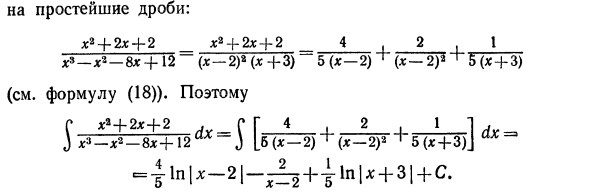
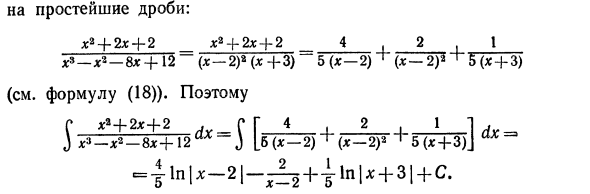

Интегрирование рациональных функций
- Рациональная интеграция функций. Некоторая полиномиальная информация В этом разделе мы кратко рассмотрим информацию о полиноме, который вам понадобится: Корнем многочлена P (x) является любое число a (действительное или комплексное), которое исключает многочлен.
То есть P (a) = 0. Например, число a = 2 является корнем, потому что многочлен x * — * x2-2x — 8 234-22-2-2-8 = 0. Многочлен степени n может быть выражен как произведение n линейных факторов вида x на постоянный a0-коэффициент порядка x. P (x) = a0 (x — al) (x — at) … (x — an). (12) Числа a1E a2, …, c ^ являются явно корнями многочлена P (x).
Следующая теорема верна, но принимает ее без доказательства. Людмила Фирмаль
Поэтому вам нужно вычислить интеграл / n === J ^ — ^ — y. Перепишите этот интеграл как IГdt _ 1С (t * + a2) —t2 _ 1ГРdtГl% dt 1 n J (<2 + a2) «~ a2J (/» + e «)» [J WTW ^ 1 3 (/ a + va * Обратите внимание, что мы получаем / = 1G / -G ^ 1 n ‘l-a2 L’ / j-i J (/ a-f-aa) «J * v ^ г / с t2dt Примените частичное интегрирование к интегралу j yi ^^ n и установите u = t, du = dt, do-.J 2 \ ii * v-1 (/ 2 + a2) / i »2 (1-l) (/ a-fa ‘) * -1’ C t1 dt t___1_ C dt J (* a-faa) a 2 (1-n) (/ 2-f-a2) «~ l 2 (i- / 7) J + «! / 2 (1-l) (/ * + aa) l-1 2 (1-n) n ~ 1 ‘ Подстановка найденного интеграла в выражение (*) дает: = a2-2 (I-a) (/ a + aa) «-1» ^ 2 (1-n) = 1 £ 1 так / _L G2 * -3 / | ? _ 1 / ч n a2 12n-2 и — «1 ‘2 (i-1) (/ a4-fl2)» — 1J * Полученное выражение называется приведенным выражением. Покажем приложение с примером. Пример. Поиск / 8 = |) 3. Решения. Где а = 1, л = 3. Используя формулу () / 1Г23-3 /, «1-3 / 1» 3 ~ la 12 • 3-2 a 2 (3-1) (/ a-f-1) 2J 4 2 4 (/ 2-f-1) 2 ‘, но в той же формуле ()
‘l = j ?? £ l = arctan <+ c (/ a = TarCtS / + 2FFI) + C’ немедленно /. [tarctS <+2 (PM)] + C = 4 (** + 1) 3 1 8 (GP-O 1 8 Поэтому, чтобы завершить задачу интегрирования рациональных дробей, остается найти способ разложить правильную рациональную дробь в простейшую дробную сумму. 4. Разложение простых рациональных дробей на простые дроби Выше (см. Подраздел 2) показывает, что рациональные интегралы сводятся к полиномиальным и обычным рациональным интегралам. Теперь мы узнаем, как все в порядке P (x) Сильные рациональные дроби можно разбить на простые дроби.
| Неопределенный интеграл и его свойства | Интегрирование тригонометрических функций |
| Основные методы интегрирования | Интегрирование некоторых иррациональных функций |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Существенное значение при разложении нормальной рациональной дроби ^ у в простую дробь Разложите знаменатель дроби Q (x) на произведение линейных и квадратных факторов (см. Подраздел 1). Для ясности предположим, что знаменатель Q (dc) учитывается следующим образом: Q (x) = (x-a) k (x-b) 1 (x2 + px + q) m, Здесь квадратный трином не имеет реального корня. Далее справедлива следующая теорема, которая дается без доказательства. P (x) Теорема правильной дроби 757-7, где Q (x) = = (X — a) k (x — b) 1 (x2 4-P * 4-q) m * можно однозначно разложить в простейшую дробную сумму. P (*), Ak B, B2 v, Q (x) * -a (x-ay » ^ (x-a) — x-b (x-bY «* 1 (x-b) 1 T, MjX + iVjM2x + M2, Mmx + Nm P4. T, U2 J. I lT ••• T / „2 |.» I «W» U4 / x * + px + q 1 (x * + px + q) * ….. (x * + px + yau
Где Ait B {, Mj, Ni — действительные числа (i = 1, 2, …) Уравнение (14) показывает, что простейшие дроби типа I и II соответствуют линейным множителям знаменателя Q (x), а простейшие дроби типов III и IV соответствуют квадратным множителям. Кроме того, число простых дробей, соответствующих конкретному фактору (линейному или квадратному), равно степени, в которой этот фактор включен в факторизацию дробного знаменателя.
Обычные рациональные правила разложения дроби действительны для любого конечного числа линейных и квадратных коэффициентов, включенных в знаменатель Q (x) разложения. Людмила Фирмаль
Метод неопределенных коэффициентов Одним из самых простых способов определения простейшего коэффициента нормальной дроби является метод неопределенного коэффициента. Давайте рассмотрим пример применения этого метода. Пример 1. Разложить на простые дроби х * -5х + 9 (х-1) * (** + 2 * + 2) ‘ Решения. Применим уравнение (14). x2 — T> x + 9 Ax A2 Mx + N Pr, (X-l) 2 (x24-2x-f-2) x-1 ^ (x-l) 2_t ~ x24-2 * 4-2 » Где Alt A2, M и N — все еще неизвестные числа. Приносит правую часть тождества (15) к общему знаменателю. x2-5x -} — 9 A x (x-1) (x2-f-2x — {- 2) -} — A.2 (x2 — {- 2x-f-2) -f- (Mx-f- N) (х-1) а (X-I) 2 (x2 + 2×4-2) ~~ (x-I) 2 (x2-2x + 2) В этом тождестве дробный знаменатель одинаков.
Поэтому числители должны быть равны и равны. x2-5x + 9 = Ax (x-1) (x2 4-2x + 2) 4- + A2 (x2 4-2x + 2) 4- (Mx 4-N) (x-1) a. Расширяя скобки и помещая полином справа от последнего уравнения, которое уменьшает степень x, получаем: l: 2-5l: 4-9 = (Ar 4-M) x ‘4- (A, + l2-2m 4-N) x2 + 4- (2 Ar 4-m-2N) x + (-2At + 2A2 + N). Два полинома только в том случае, если степени равных степеней x равны и они равны друг другу. Если вы сделаете коэффициенты этих многочленов равными друг другу равными степенями x, вы получите систему уравнений. х3: L, 4-М = 0; ^ x2: топор + A% -2M + iV = 1; I Для х: 2Ar + M-2N = -5; G Бесплатное членство: -2A1 + 2Ag + L = 9. Я Решение этой системы приводит к следующему *
A2 = 1, M-J, A7-J. Подставляя найденное значение в уравнение (15) вместо Л2, М, N X2_5X_ | _9 7.1, 7×4-21 (16) (X-1) 2 (x242l: 42) 5 (x-1) 1 (x-I) 2 ^ 5 (x24-2 * +2) * Пример 2. Разложение на простые дроби x2 4-2x 4-2 (x-2) 2 (x-b3) ‘ Решения. Поскольку знаменатель имеет только корни действительных чисел, форма дробного разложения согласно уравнению (14) 4-2 * 4-2 A, _ Ajz _, B, (X — 2) * (x4-3) — x — 2 ‘(x — 2) 3’ x-f-3 ‘k’ Возьмем правую часть отношения (17) как общий знаменатель: x’2-f-2x-f-2 ^ (x-2) (x + 3) 4-L2 (* 4-3) 4-Bt (x-2) * (x-2) 2 (xj-3) ) (X-2) 2 (xf-3) Если числители равны, x2 + 2 * 4-2 = Ar (x-2) (x + 3) + Λ (x + 3) 4-Bx (x-2)
Уменьшите степень x и поместите многочлен с правой стороны \ c * + 2x + 2 = (A1 + B1) x * + (A, 4-Ar-4B1) x — {- (- 6A1 — \ — Za — \ — 4B1). Выравнивание одинаковой степени коэффициентов в правой и левой частях уравнения дает систему уравнений Ar + B ^ l. -6L, 4-3, 4-4c, = 2. 4 1 Решение этой системы приводит к Ar = 2. Подстановка найденных значений коэффициентов в отношение 17) дает следующее: га 4- 2х 4- 2 _ 4 2 1. (* -2) «(* 4-3) 5 (x-2) (x-2) 2-r5 (x4-3) * K) Пример 3. Разложение на простые дроби 2l: 24-10x — 18 (x-1) (x + 2) (x-3) * Решения. Используйте формулу (14), чтобы получить идентичность
2 * 3 + 10 * —18, ^ A B C (x-1) (x + 2) (* -3) до x-i + 2 + 3 * Сократите идентичность до общего знаменателя с правой стороны, сделайте равными правый и левый числители и получите идентичность 2x * + 10 * —18 = A (x + 2) (x-3) + B (x-1) (x-3) + C (x-1) (* + 2), (19) Откуда 2n: 2 + 1 (k-18 = * (+ + + + C) ;; 2 + (— 4H + C) x + (-6 Л + 3B-2C). Выравнивание коэффициента мощности одного и того же x дает систему уравнений A + B + C = 2 -А-4В + С = 10, -6L + 2> B-2C = -18, Найдите A = 1 отсюда. Б = -2, С-3. Таким образом, 2×2 -f 1 Oh-18 _ 2 , 3 (Х — 1) (х- | -2) (х-3) х— 1 х + 2 ‘х— Во многих случаях поиск фактора разложения может быть значительно упрощен. В самом деле, рассмотрим пример, приведенный сейчас. Формула (19), полученная там 2x + 10x — 18 = A (x + 2) (x-3) + B (x-1) (x-3) + C (x-1) (x + 2)
Действительный идентификатор для любого значения х. Выберите значение для x, чтобы уравнение (19) принимало простейший вид. Здесь проще всего взять один из корней знаменателя для x. Если х = 1, А = 1, значит, -6 = 6А. Аналогично, установка x = 2 приводит к 30 = 15B и B = -2. х = 3 30 = 10 ° С, С = 3. Показанный метод особенно полезен, когда нормальный рациональный знаменатель Q (x) имеет только реальные простые корни. На практике оба вышеупомянутых метода часто комбинируются. Пример 4 «Разложить на простые дроби х2-ф-х + 13 (X_1) (x * + 4) — Решения. Используйте уравнение (14) для получения: x3 + x-t-13 _A Mx — \ — N (x-l) (x2-H) x2-f4 • После уменьшения правой части уравнения до общего знаменателя и приведения равных правого и левого числителей,
l: + 13 = A (x2 + 4) + (Mx + N) (x-1), (20) IL I x2 + l: + 13- (L + L1) га + (-M + N) x + 4L-N. (20 ‘) Предполагая, что x = \ 9 в уравнении (20), 15 = 5A и A = 3. Обратите внимание, что коэффициенты x2 и x равны и Λ = 3 3 + M = 1,) -M — \ — N = 1, / М = -2, Н = -1. Открытие Пример 1. Вы можете легко проверить следующее 5l; 4-40xs + 115×2-140l: + 60 = 5 (x-2) (x-2) (x-1) (x-3). Пример 2. Полином x3 + l: 2 + 9x + 9 = (x + 1) (x-3t) (x + 30. Некоторые из линейных факторов, из которых разлагается полином, являются одинаковыми. Вы можете объединить те же факторы в расширении (12) и использовать следующий формат: P (x) = a0 (x-a) k> (x-6) 4. , (X- /) H (12 ‘) Если все маршруты a, 6 и / разные, k1 — \ — kt-] … … + kt = n.
Корень a многочлена P (x) называется корнем кратности kx, поскольку линейный множитель разложения (12 ‘) встречается fe раз. Корень разнообразия единства называется простым. Так, например, многочлен P (x) = 4 (x — 2) 3 (x — 1) 2 (k — 5) имеет следующие корни: a – 2, b — 1, c = 5, 2 — кратность корня 3, (-1) — кратность 2, 5 — простой маршрут. Алгебра доказывает, что если многочлен с действительными коэффициентами имеет корень комплексного числа y = a-fp с кратностью k, то сопряженное комплексное число y = a-fii также является корнем того же многочлена кратности.
Если полиномиальная факторизация включает множитель (x — y) k, соответствующий комплексному корню Y = »a + p /, то это разложение имеет множитель (x — y) k, соответствующий сопряженному корню y = a — pi , , Умножьте эти два фактора, соответствующие сопряженным корням. (Xy) k (xy) * = [l: — ( — 2a, <7 = a2-fP2. Следовательно, произведение линейных факторов, соответствующих сопряженным корням, можно заменить квадратным троичным выражением с действительными коэффициентами. Все вышеперечисленное позволяет сформулировать следующие цели:
так x * + x-fl3 s__2x4-1 (X — 1) (x24-4) l W + l * 6. Разумная дробная интеграция Все вышеперечисленное в предыдущем абзаце позволяет сформулировать основные правила интегрирования разумных дробей. 1. Если рациональная дробь неверна, она выражается как сумма многочлена и нормальной рациональной дроби (см. § 2). Следовательно, нерегулярные рациональные интегралы являются полиномиальными и нормальными рациональными интегралами. 2. Фактор правильный дробный знаменатель. 3.
Правильная рациональная дробь разбивается на простейшую дробную сумму. Таким образом, нормальное рациональное дробное интегрирование является простым дробным интегрированием. Давайте посмотрим на некоторые примеры. ПтхлУСх * -Зх3-5х24-30х-22, Пример 1. Поиск \ — ^ — ух — ^ — дх. Решения. Под интегралом указывается неверное рациональное число. Если вы выберите целую часть, х * —Зх3-5х24-30х-22 _ 9 x24-2x-f-2х3 — х — 8х4-12 + х3-х2-8×4-12 » так Px * -3×3-5×24-ZOx-22, J x3-x2-8×4-12 ах = S hH ^] — ^ + ^ x3 — x2-8x4x4 = (x — 2) a (x4-3), расширяя обычную рациональную дробь x2 4-2×4-2 _ x34-2×4-4 x9 — x2-8x 4-12- (x-2) 2 (x4-3)
Простая дробь: x2-j-2x-j-2 _ x * + 2x + 2 = 4, 2 1 x * — x * -8x + 12 до (x-2) * (x +3) 5 (x-2) + (x-2) a + 5 (x + 3) (См. Уравнение (18)). так C ** + 2x + 2. C D 4 2__1_1 д J x * -x * -8x + \ 2aX-) [b (x-2) ‘(x-2) 2 1 5 (* + 3) J c = | ln | x-2 | — ^ + i-ln | x + 3 | + C Так в конце концов RDG ‘—ZX3 —5×2-f-30x — 22 Av _ J d; s_x2-8D: поиск -b12 aX ~ Пример 2. \ Решения. Существует правильное рациональное число под интегралом. Разбейте его на простые дроби (см. Уравнение (16)) и получите x2-5x + 9 _ 7 1 7l + 21. (X-I) 2 (x2-f-2x-f-2) 5 (x-1) (x-I) 2 5 (x2-f-2x + 2) ‘ так p x2-5x + 9, 7 C dx C dx 7 C x + 3. J (x-1) 2 (x2 -f- 2x — {- 2) 5 Jx-1 + J (* -l) 2_h 5 J x22x-f-2
Для последнего интеграла в правой части равенства И, подставив / = y {x24-2x- | -2), вы получите его как известно (см. Раздел 3) \ В результате x = t-1, dx = dt, x2 — {- 2x-f2 = / 2 + 1. тогда 4-2 arctan / -f- C = y In (x2 -f-2x + 2) -f2 arctan (x + 1) — {- C. Поэтому мы имеем i 2) ^ = -Уln1 ^ 11-, 4м 4- ^ In (X2 + 2x + 2) + + y arctg (x-f 1) 4-C.
Точное предложение, в котором можно избежать мнимых чисел путем разложения многочленов. Полиномы с действительными коэффициентами можно выразить в виде P (k) = ae (x — a) <* (x — b) *> … (xa + pxx + q (x * + p * x 4-q) k … В этом разложении линейный множитель соответствует действительному корню, а квадратный трехчлен соответствует комплексному корню многочлена. Константы a0, a, b, .plt qv … являются действительными числами.
Разумные дроби. Соответствующее рациональное выделение дроби Как вы знаете (см. Гл.1, §4, стр.7), дробная рациональная функция или просто рациональная дробь — это функция, которая равна частному от деления двух полиномов. RT (х) R M Qn (x) ‘ Где Pm (x) — многочлен степени m и Q, t (x) — многочлен степени n. Пример: Рациональное число называется правильным, если порядок числителя меньше, чем порядок знаменателя. В противном случае рациональные числа называются неточными. Вышеприведенное рациональное число неверно.
Цель этого раздела — представить способ интегрирования рациональных дробей. Во-первых, обратите внимание, что нерегулярное рациональное число может быть выражено в виде суммы полинома и обычного рационального числа. P fx) Конечно, давайте — неправильно, рационально Доля, то есть порядок P (x), больше или равен порядку Q (x). Разделите числитель на знаменатель, чтобы получить идентичность P (x) -Q (x) L (x) = r (x), Где L (x) и r (x) — многочлены, а порядок остатка r (x) меньше, чем знаменатель дроби Q (x). Отсюда Q (x) b ‘ T fx) Где правильная рациональная дробь. Например, пусть /? (*) = -Tr ^. Разделить x * — \ — bx-6x — \ — b В xe + 2x-1 получим частное Tx) = x ~ \ ~ 5 и остаток r (x) = -2xr-15x + 10 .. Таким образом,
x * + bx * —6×4-5 _, г, -2×2-15l-4-10 x3 + 2x-1 ‘x3 -f- 2x-1’ Следовательно, нерегулярный рациональный интеграл P (x) Дробь сводится к интегралу многочлена L (x) и нормальной рациональной дроби I tu ** = HL «+ ffi] ** = IL» ■ * ■ + Jт1 Поскольку вы можете интегрировать полиномы, вам нужно рассмотреть нормальную рациональную интеграцию дробей. Как мы увидим ниже (см. Раздел 4), нормальная разумная дробь может быть выражена как сумма конечного числа так называемых простых дробей следующих четырех типов: I.-; II. r — ^ — i (n ^ 2, 3, …); III. IV. , + ‘(Rt −2, 3, …), Где A, a, p, q, M и jV — действительные числа и троичные x8 + p * + <7
Реального корня нет, то есть ^ -q <0. Таким образом, Научиться интегрировать простейшие дроби и разбивать правильную рациональную дробь на простейшие дробные суммы решает проблему интегрирования рациональных дробей. 3. Простая рациональная дробная интеграция Интеграция простейших частей типа I и II несложна. На практике: I- * I (* — *> — «<* (* — ‘) = (■ -„) (? — „)» -‘ + C- Далее рассмотрим рациональную дробную интеграцию типов III и IV. Привет там J x * + px + d Рассмотрим знаменатель x1 — {- px4-q по отдельности и добавим x2 + px к полному квадрату. По гипотезе троичный x2 + px + q не имеет действительного числа, поэтому
pi p2 корней, то выражение q—> 0. Вводит обозначение q— =. Затем примените изменение переменной к интегралу Отсюда x = / — |, dx = dt, x * + px + q = (x +% y + (q- y) = t * + a \ так Jxt + px + q J / 24-a3 J + a2 1 + J W => ^ + * ‘> + arctan 1 + C Наконец, заменив выражение t h a hx, Я dx = In (* »+ px + q) + — = L = arctg- + C JTpx + q 2 v 47 G rg & f pi ‘ Вы есть J Пример. Найти 3x + 5 х * 4-2×4- U Решения. Введите новую переменную и задайте для нее половину производной знаменателя (см. Сноску на стр. 305). тогда t 4-2x-fl0) ‘= x4-1, x = t-, dx = dt. x * + 2x + 10 = (/ -1) a4-2 (/ -1) 4-10 4-9. так Используйте Sjfl 3×4-5 rfv-fSe-O + idt.o__ J x44-2×4-10 J + 9 + J / * H-9 ~ = | В 4-9) 4- для арктана + C = | В (* «4-2 * 4-10) + arctg4- C. • J Внутривенно \ ,,, Mx + «DX. Введите новую переменную / как в случае III. x = dx = dt, x * + px + q = t * + a \
И ry Где, как указано выше, cr-q- ГMx + N dxМСtdt / МР \ гдт J + + — / UJ + Г2 J J (/ «n-in») — ‘ Первый интеграл соотношения (13) легко вычислить. I (TOG = «AND» ‘+ «‘> -» << С1 + **> — ^ — „н ^ у-х +

