Оглавление:




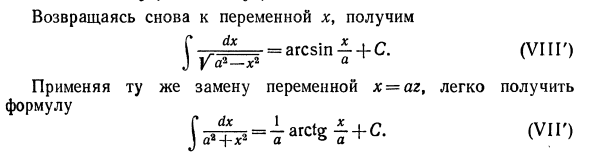

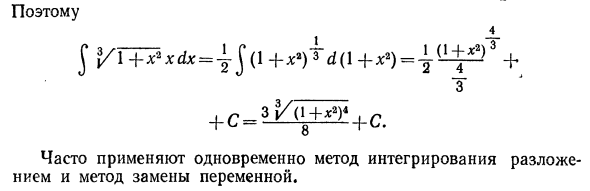



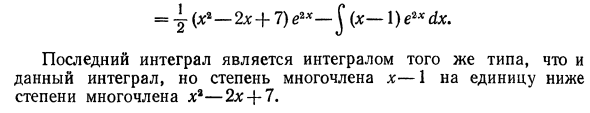

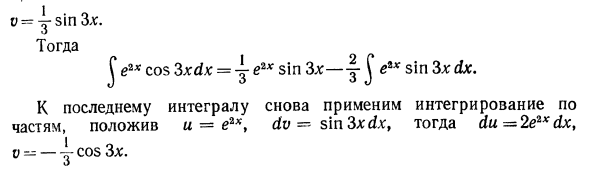

Основные методы интегрирования
- Основной метод интеграции Вот несколько хитростей. Во многих случаях данный интеграл может быть приведен к табличной форме. Такими методами являются интеграция с помощью декомпозиции, интеграция с помощью замены переменных и интеграция по частям. /. Интеграция разложения Этот метод основан на разложении подынтегральной функции в суммы функций, из которых вы можете найти другие производные, используя другие методы. Вот самый простой пример. Пример 1. Поиск [x 2dx.
Решения. Есть несколько возможностей. Установка u = s \ nx, dv = xdx, du = cos xdx, v = с использованием уравнения (11) j x sin x dx = ~ sin x — i- J x2 cos * dx. Разделение этого интеграла на произведение двух факторов следует рассматривать как неудачу, поскольку это приводит к более сложной интеграции.
Например, вы можете поместить and = sinx, a xdx = dv; u = x и sinxdx-dv. ртуть Людмила Фирмаль
Положите отсюда u = x, dv-sin xdx \ и найдите du-dx, v = -cosx. Используя уравнение (11), J x sin x dx-x (-cos l:) — J (-cos x) dx = -x cos x — \ — ^ cos xdx. Ho ^ cos xdx = грех x -f-C. Итак, наконец J xsmxdx = — * cos; c-f sinx-f C. Иногда необходимо объединить детали несколько раз подряд, чтобы получить окончательный результат. Я укажу некоторые из часто встречающихся интеграций, рассчитанных методом интеграции для каждой части. I.
Смотрите интегральное J P (x) e * x dx, JP (x) sin kx dx, \ P (x) coskx dx, Где P (x) — многочлен, а k — конкретное число. Если u = P (x), эти типы интегралов частично усваиваются. Пример 2. Найти J (x2-2x + 7) e2xdx. Решения. u == x2-2x + 7, dv-e ** dx, затем du = (2x — 2) dx, v = -> e2x. Используйте интегральную формулу детали, чтобы получить (X2-2x + 7) e2 * dx = ~ (x2-2x + 7) e2 * -C \ e2x (2x — 2) dx = = j (x * -2x + 7) e2x-§ (x- ) e2xdx. Последний интеграл того же типа, что и данный интеграл, но порядок многочлена x — 1 на порядок меньше, чем порядок многочлена ha — 2x + 7.
| Некоторые теоремы о дифференцируемых функциях | Интегрирование рациональных функций |
| Неопределенный интеграл и его свойства | Интегрирование тригонометрических функций |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Установите u = x— [, dv = e2xdx и повторно примените интеграл по частям к интегралу ^ (x — ) exxdx. Тогда du-dx, i / = ye2 *. У нас есть ^ (X- ) e * xdx = -j (x— ) e ** до ^ e ** dx = ± (x— ) e * x— + j (x2-2x + 7) e2xdx = ± (x * -2x + 7) e2x— [± (x — l) e2x-i <? **] + II. Показать интеграл ^ P (x) \ n xdx, J P (x) arcsin x dx, J P (x) arccos x dx, P (x) arctg x dx, J P (a 🙂 arcctg x dx, Где P (n 🙂 — многочлен от x. Во всех этих случаях используйте функцию, которая вызывает P (x) при интеграции в деталь и при интеграции в деталь. Пример 3. Поиск J (4 * ® + 6 * -7) с помощью xdx.
Решения. Интеграл вида Je «* cosbxdx, ^ eaxs \ nbxdx. Где а и б Числа. Эти интегралы можно найти, интегрируя дважды на часть. Давайте рассмотрим пример. Пример 4. Найти Jе2хcosЗхdx. Решения. u = e2x, du = cos 3xdx *, duce du = 2ex dxto = y sin 3 *. тогда Если J e2x cos 3xdx = e2x sin 3x — j J eix sin 3x dx. Повторно примените частичную интеграцию к последней интеграции, и = e2xt dv = s’mSxdx, du = 2e2xdx, у — cosЗа;
Поместите s = 1n *, dv- (4 * 3 — {- 6x-7) dx \, затем du = j, v = x4 + 3×2-7x. Формула (11) град: J (4l: 3 + 6jc — 7) In xdx = (chl + 3×2-7x) lnx— [* 4-P * 2-7 * dx = III. Людмила Фирмаль
так j e2x sin 3xdx = — ~ e2x cos 2> x + j e2 * cos 3x Je2 * cos3xdx = для e2 * sin 3x — (-для e2xcos3x + для j cos3xdx *), или J e2 * cosЗл-dx = уe2x (sin 3x + cos 3 *) — 4 J cos 3 * ^ Справа от последнего отношения находится искомый интеграл Jе2хcos3xdx. Двигаться влево (* + J) e2Xcos3xdx = ye2x (sin3x + cos3x) e Отсюда j e »cos 3x dx = <» (3s.n3x + 2cos3 *) Результирующая функция является одной из обратных производных функции 62 * cos3; c. Чтобы найти все антипроизводные, добавьте произвольную постоянную C справа. J e «COS 3xdx = ^ (3sin3, + 2cos3x) + s Далее рассмотрим интеграцию определенных типов базовых функций. В то же время систематически используйте общие методы интеграции, описанные в этом разделе.
r »m x3 — \ — 4x — \ — 2 1,. о, 1ГХя + 4х + 2. Решения. Когда -C: — = x2 + 2-4—, \ —-C * -ajc = 2x 2 1’x J 2x + 2 + + = | + 2x + ln | xl + + C = £ + 2x + 1n | x | + C Проверка: Там не будет никаких дальнейших проверок. Тем не менее, рекомендуется, чтобы читатели сделали это в первую очередь для самоуправления. Пример 2. Найти fjgp ^ nre Решения. У нас есть dx_rcos2x-f-sin * Xjx = Cf 1, 1 . _ J cos2xsin * x J cos’-xsin2 * -J Vcos2 * ‘sin2 * /’ ~ = \ —Z- + \ -r4- = ^ <ХX — ctg * — | -C. J cos2 * 1 J sin2 X и b I После успешной разработки подинтегратора мы сократили интеграцию до табличной интеграции (уравнения (V) и (VI)). Далее давайте перейдем к другим методам интеграции. 2.
Интеграция методом подстановки переменных Во многих случаях можно ввести заданный интеграл J f (x) dx вместо интегральной переменной x с новой переменной z. Новые интегралы, которые включены в таблицу основных интегралов или которые легко вычисляются иначе. Этот метод интеграции называется методом замены переменных или методом интеграции замены.Вместо x мы вводим новую переменную z, связанную с x соотношением * =
‘(*) cfe. (7) Выражение (7) называется выражением подстановки переменных. Чтобы доказать справедливость уравнения (7), достаточно убедиться, что производные обеих частей явно равны. Различение левой стороны отношений (7) d ) f (x) dx = f (x) dx Однако, поскольку x = (p (r), dx = η> (r) dz. d \ f (x) dx = f [y (z) W (z) dz. (8) С другой стороны, если мы различаем правую часть соотношения (7), d \ f [Φ (r)] Φ ‘(r) dz = f [Φ (r)] Φ’ (r) dz (9) Отношения (8) и (9) d \ f (x) dx = d \ f [y (z)] y ‘(r) dz. Таким образом, справедливость уравнения (7) доказана. Предположим, что найден правый интеграл соотношения (7). Дай мне $ f [<P (*)] <P ‘(2) ^ = Ф (2) + С. Отсюда легко найти необходимый интеграл как функцию от x.
Для этого решаем уравнение x = φ (r) для r. То есть найти обратную функцию z = co (x) и присвоить ее Φ (r) *: J / (*) ** = $ / [<p (r)] <p ‘(rMr = Φ (r) + C = Φ [ω (*)] + £. Замечания. Уравнение (7) легко запомнить. Ее право Замените x на φ (r) с интегралом J f (x) dx и замените dx Φf (z) dz. Вот пример: Пример 1. Найти \ r dx J Va2- * 2 Решения. Найти x = az, dx = adz. Используйте уравнение (7) для получения: D dx = ad adz = d dz. J J Ya * —a * r * ~ J VT ^ V * ‘ P dx Однако j t = arcsinz -} — C, в соответствии с формулой VIII, § 1, пункт 3. Следовательно, Г ^ dx = \ rdz-arcsin z — {- C.
Вернитесь к переменной x снова и получите дх арксин- + с. (VII D) 2-х2 в Применяя такое же изменение в переменной x = az, легко получить выражение Я Пример 2. Найти ^ sin axdx. z dz Решения. * = -, Dx = -и применяя уравнение (7), JDZ 1G 1 I sin z — = — \ sin zdz = -cos z — \ — C to —cos ax -J- C. a a j a 1 a Рассмотрим другой способ применения выражения замены . Если интеграл является комплексной функцией, умноженной на производную внутренней функции, то есть форма интеграла Для f [φ ()] φ ‘(x) dx это интегрирование может быть упрощено, если Заменить внутреннюю функцию новой переменной z = φ (x).
Фактически, когда применяется выражение для подстановки переменных (7), оно становится следующим. $ / [φ (*)] φ ‘(x) dx = \ f (z) dz Обратите внимание, что результирующее выражение отличается от выражения (7) только спецификацией независимой переменной. Пример 3. Найти ^ tgxdx. Решения. \ tgxdx = ^^^ Есть дх. Обратите внимание, что sinxdx => = -dcosx и введите r-cos *. тогда = -In | cos a: I-C. Вот так Jtgxdx = -In | cos x | -f- S. (XV) Точно так же, $ ctgхdx = In | sin x | + S. (XVI) Приобретая навыки во время интеграции путем подстановки переменных, можно не выполнять все вычисления подробно с самой простой интеграцией. _ Пример 4. Найти J jj / l -f- x2xdx. Решения. Если мы сосредоточимся на 4Tod (\ + x2) = 2xdx, мы получим xdx — ^ rd (\ — \ — x2).
так J yT + 72 Xdx = 1 j (1 +) ■ Гd (1 + * •) = 1 (I ± f33 T Во многих случаях метод интегрирования и метод подстановки переменных используются одновременно. Рассмотрим форму интеграла J sinmx-cos rtxdx, J sin mx-sin nxdx, J cos mx-cos nxdx. Эти интегралы вычисляются методами разложения, основанными на тождестве тригонометрической функции sin (m + n) x-f-sin (m-n) x sin mx-cos nx = —————— ^ -1-—; cos (m-n) x — cos (m-n) x sin mx-sin lx = ———— g —— 1——; cos (m -f n) a: -f cos (m -n) x cos mx • cos nx = –1 — ^ — 1––.
Пример 5. J sin 2x-cos6xdx = y ^ [sin (2 — {- 6) x — {- sin (2-6) x] = yj sin 8x dx-y ^ sin 4xdx = ^ j sin 8x d (8x ) -Y ^ sin 4xd (4x) = = — ^ cos8x + y cos 4x + C Интеграция без частей Пусть u = u (x) и v = v (x) две функции x с непрерывным дифференцированием. Из дифференциальных расчетов видно (табл. VI, см. Уравнение (65 ‘)) д (уф) = удв + вду. (10) Объединение равенства с обеих сторон (10) ^ D (УФ) = ^ и DV-J- J V ду или J и DV = JD (УФ) -J V ду Ho J d (uv) -uv — \ — C, поэтому J udv = uv — J vdu. (11)
В формуле (I) неопределенный интеграл, содержащий произвольную постоянную, остается в правой части формулы, поэтому произвольная постоянная C не записывается. Уравнение (11) называется интегральной формулой для каждой части. Вы можете свести интегральное вычисление ^ udv к вычислению интегрального J vdu. Это часто Более просто. Давайте рассмотрим пример применения этого метода. Пример 1, [x sin xdx.

