Оглавление:












Неопределенный интеграл и его свойства
- Неопределенные интегралы и их свойства /. Примитивные и неопределенные интегральные понятия В дифференциальном расчете были решены следующие основные проблемы. Найти производную определенной функции. Многие проблемы науки и техники приводят к постановке обратной задачи об ионах: для заданной функции f (x) найдите функцию F (x), производная которой равна заданной функции f (). F ′ (x) = f (x). (1)
• (2) Функция F (x), которая связана с функцией f (x) соотношением (1) или (2), называется ее обратной производной. Таким образом, следующее определение было достигнуто. Определение Примитивная функция заданной функции I (x) — это функция, производная которой равна заданной функции или производная которой равна выражению I (x) dx.
Поднятый вопрос может быть сформулирован в следующей эквивалентной форме: Для конкретной функции f (x) найдите функцию F (x), разность которой равна определенному выражению f (x) dx. dF (x) = f (x) dx. Людмила Фирмаль
Так, например, обратная производная функции / () = * x2 становится функцией г. (X3 V F (x) = -g, ^ (*) = (y) = x3, или что то же самое dF (x) = d ^ = xi dx. Поиск примитивов с помощью этой функции является одной из основных задач интегральных вычислений. Естественно, возникают следующие вопросы: Есть ли у функции примитив? Положительный ответ на этот вопрос для достаточно широкого класса функций дает следующая теорема. Теорема 1. Функция, продолжающаяся в сегменте, имеет примитив * в этом сегменте.
I. ^ xndx = + C (nF-1) VII. j- | L3 = arctgjc + C Особенно, когда n = 0: VIII. J ^ == = arcsinx-j-C =. IX. = ^ + II. ^ = \ n \ x \ + C. X. + III. ^ s \ nxdx = -cosx + C. XI. Jshxdx = chx + C Внутривенно J cosx tfx = sin x -f C. XII. J ch l: dx = sh x -f C. V.Ji5s- ^ + C. Xiii. J ^ L-thx + C. • laSi-ctex + C. Xiv. J ^ -cthx + C VI Вывод этих уравнений приводит к проверке того, что разность в правой части равна подынтегральному выражению в левой части уравнения и не является трудной для всех, кроме второй.
| Векторная функция скалярного аргумента | Основные методы интегрирования |
| Некоторые теоремы о дифференцируемых функциях | Интегрирование рациональных функций |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Докажем справедливость формулы (II). Подынтегральное выражение определено для всех ненулевых значений x и является непрерывным. Если *> 0, \ x \ -x и In | x | = In l;. Согласно известному дифференциальному уравнению d \ n \ x \ = d \ nx = -. Так что, если х> 0 J j = «lnx + C = ln | * | + C * Если <0, | x | = i-x и In | n: | = ln (-x). Однако dIn (- *) == — dx «= -. Поэтому * <0 г х х Jf = ln (- *) + C = ln | * | + C Следовательно, уравнение (II) справедливо в любом случае. 4. Основные характеристики неопределенных интегралов Дает два свойства неопределенных интегралов.
Свойство А. Неопределенный интеграл алгебраической суммы конечного числа функций индивидуально равен алгебраической сумме неопределенного интеграла каждого члена. [[/ (*) + G C *> — Φ ()] dx = \ f (x) dx + \ g (x) dx-Jφ () dx. (А) Свойство Б. Постоянный коэффициент можно извлечь по знаку инвариантного интеграла. \ ikf (x) dx = k ^ f (x) dx (B)
Это значительно расширяет возможности применения базовой формулы таблицы интеграции. Людмила Фирмаль
(Предполагая постоянную CFD). Уравнения (A) и (B) следует понимать в том смысле, что левая и правая части отличаются в определенных терминах. Таким образом, чтобы установить справедливость этих уравнений, достаточно показать, что левая производная (или производная) равна правой производной (или производной) (глава 6, § 6, пункт (См. 3). Например, докажите эффективность равенства (B). Дифференцируя левую часть (B) уравнения и применяя уравнение (4), d ^ kf (x) dx = kf (x) dx. Дифференцируя правую часть (B) уравнения, d (feJf (x) dx) = kdJ / (x) dx = k [(x) dx.
так d \ jkf (x) dx = d (k $ f (x) dx), Уравнение (B) следует. Пример * Найти J (x3-f-3sinx — 8) dx. Решения. Когда вы применяете свойства (A) и (B): J (x3 4-3 sin x-8) dx = $ x3 dx + 3 $ sin x dx — 8 J dx. L uz + 1 u4 Но] xMx = zTT + C1 = ^ — + C1 (см. Формулу (I)). Согласно формуле (III), 3 ^ sin xdx = 3 (-cosx- | -C2) = -3cosx-fЗС2. 8 J dx = 8 (x-b C8) = 8x 4-8C3. Вот так J (x3 + 3 sin x-8) dx = 3 cos x — 8x + (Ct 4-ЗС, –8CJ. Каждая интеграция получила свою произвольную постоянную. Однако, если C19 C2 и C3 — произвольные постоянные, C = C1 + 3Ca-8C3 — также произвольная постоянная, поэтому в конце описывается только одна произвольная постоянная. Итак, наконец: J (x34-3 sinx — 8) dx = ^ -3cosx — Sx + C. Точность полученных результатов легко проверяется дифференцированием. конечно d (j — 3 cos x — 8x + c) = (x3 + 3 sin x − 8) dx.
Если в функции, выполняющей поиск антипроизводных, имеется точка останова, учитывайте ее только в интервале, где она непрерывна. Задача поиска антипроизводного той или иной функции не решается однозначно. На самом деле, например, Chx) —xg, Хз х5 Ее антипроизводной является не только у, но у-F6. Х3 х3 И «3 + 9, и, как правило, y + C, где C — произвольно выбранная константа, так что, конечно, проблема в нахождении всех антипроизводных данной функции. Следующая теорема дает исчерпывающий ответ на этот вопрос.
Теорема 2. Если функция F (x) является обратной производной функции f (a *) отрезка a ^ x ^ 6, все другие обратные производные функции f (x) отличаются в постоянных терминах от F (x) вы. Это выражается как F (x) + Ct (C является константой). Доказательство. Пусть Φ (x) — другая антидифференциальная функция функции f (x), а Φ ′ (x) =? ‘(X) = f (x). Однако, если производные двух функций на сегменте равны, разница между этими функциями постоянна для этого сегмента (см. Главу 6, § 6, пункт 3). Φ (x) —F (x) = C, где C — постоянная.
Следовательно, Φ (x) = * F (x) + C. Это доказывает теорему. Из доказанной теоремы следует выражение F (x) + C, где F (x) — обратная производная функции f (x), C — произвольная постоянная, а все обратные производные этой функции имеют вид обложки. Здесь мы вводим понятие неопределенных интегралов. Если F (x) является одной из обратных производных функции f (x), выражение F (x) + C (C — произвольная постоянная) называется неопределенным интегралом. Неопределенный интеграл функции f (x) dx (чтение: «неопределенный интеграл на dx f (x)»). так lf (x) dx = F (x) + C. (3)
Где f (x) — подынтегральное выражение, f (x) dx — подынтегральное выражение, x — переменная интегрирования, символ -Неопределенный интегральный знак. Под знаком интеграции мы Напишите производную, а не производную искомой функции. Например, функция F (x) = -g является одной из обратных производных функции f (x) = xl, поэтому ее можно вывести из уравнения (3). Действие по нахождению неопределенного интеграла или того же самого, но по нахождению всех антипроизводных определенной функции, называется интегралом этой функции. Из определения анти-производной мы можем видеть, что производная этой анти-производной равна подынтегральной функции.
Поскольку это случай обратной производной данной функции, ее можно легко выразить как: Производная неопределенного интеграла равна подынтегральной функции, т.е. d ^ f (x) dx = f (x) dx. (4) Обратите внимание на другое свойство. Как и в случае с первым свойством, установите связь между операцией дифференцирования и операцией интеграции. Пусть F (x) — обратная производная от f (x). тогда \ f (x) dx = F (x) + C Однако f (x) dx = dF (x). Следовательно, равенство (3) часто \ dF (x) = F (x) + C. (5)
Таким образом, неопределенный интеграл производной функции равен этой функции плюс любая константа. Пример: J dx = x — \ — C, J d cos x-cos x -} — C Эти характеристики означают, что дифференциация и интеграция являются противоположными действиями. 2 геометрическое значение неопределенного интеграла Зная, что тангенс наклона касательной в каждой точке является функцией f (x) с учетом абсциссы этой точки, нам нужно найти кривую y-F (x) t. Геометрический смысл производной (глава VI, § 1, стр. Следовательно, нам нужно найти функцию F (x). F ′ (x) = f (x). (6) Соотношение (6) показывает, что искомая функция F (x) является обратной производной от / (*). Таким образом, задача была сведена к основной задаче интегральных вычислений — нахождению обратной производной определенной функции.
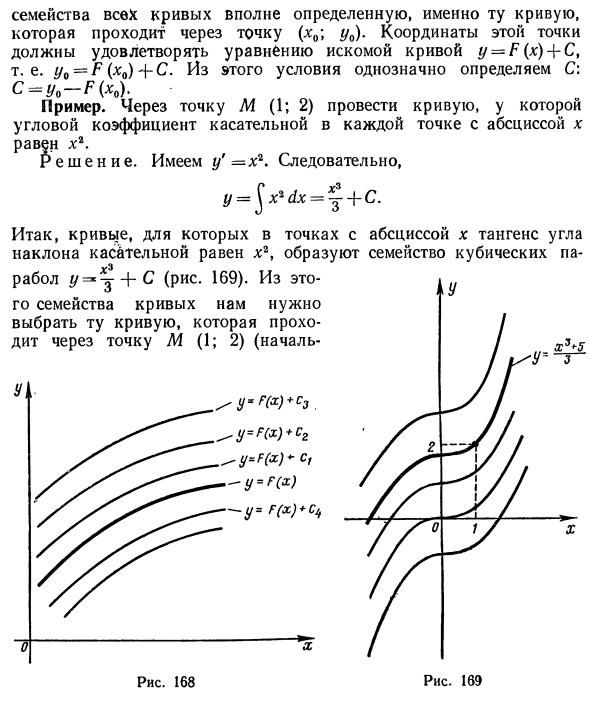
Следовательно, y = f (x) dx или y = F (x) + C. Вы можете видеть, что рассматриваемое условие выполняется серией кривых, а не одной кривой. Кроме того, если y = F (x) является одной из этих кривых, вы можете получить из нее другие кривые путем перемещения вдоль оси O (рис. 168). Чтобы выбрать только одну конкретную кривую из определенного семейства кривых, необходимо добавить дополнительное условие к условию задачи. Например, запросите, чтобы кривая прошла через определенную точку (lu, y0). Это состояние называется начальным состоянием. Устанавливая начальные условия,
Семейство всех кривых, то есть кривая, проходящая через точку (x0 \ y0), совершенно ясно. Координаты этой точки должны удовлетворять искомой кривой y = F (x) 4-C уравнению. y0 = F (x0) C. Из этого условия C: C-V0-F (x0) определяется однозначно. Пример. Нарисуйте кривую через точку M (1; 2), где коэффициент угла касания в каждой точке с абсциссой x равен x2. Решения. Здесь у ‘= х2. так Следовательно, кривая с абсциссой x и касательной к наклону, равной x2, образует кубическое семейство.
Условия). Это дает 2 =, где C =, следовательно, Узел 5 Желаемое уравнение кривой y = m + «d * — В зависимости от рассматриваемой проблемы можно найти геометрический смысл неопределенного интеграла. Вызывает график функции обратной производной функции f (x) интегральной кривой. Поэтому, если F ‘(x) = f (x), график функции y = F (x) является интегральной кривой. Неопределенные интегралы геометрически представлены всеми семействами интегральных кривых.
Все кривые в этом семействе y = F (x) + C можно получить из одной интегральной кривой, сдвигая параллельно направлению оси Oy. 3. Основная таблица интеграции Найти обратную производную определенной функции гораздо сложнее, чем найти эту производную для определенной функции. В дифференциальных вычислениях мы нашли производные основных элементарных функций (см. Главу VI) и установили правила дифференцирования сумм, произведений, частных и даже комплексных функций. Эти правила позволили нам определить производную базовой функции.
Не существует простых универсальных правил и рецептов, таких как дифференциальные вычисления, чтобы найти примитивы из элементарных функций. Так, например, даже если вы можете найти обратную производную каждого из этих примитивов, не существует специального правила для поиска обратной производной произведения, отношения двух примитивов. Способ интеграции функций (то есть, как найти примитивы) часто сводится к показу многих способов, которыми реализация может привести к целям. Для облегчения интеграции составляются так называемые базовые таблицы интеграции. Эта таблица взята из базовой формулы для дифференциальных расчетов. Вот таблица.

