Оглавление:


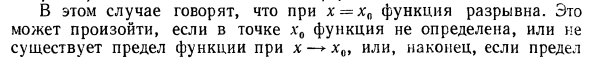



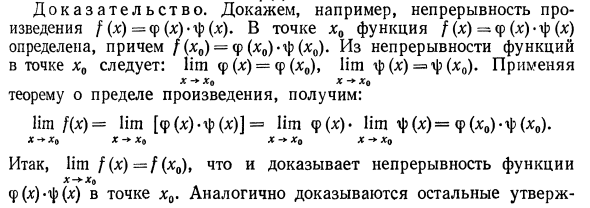

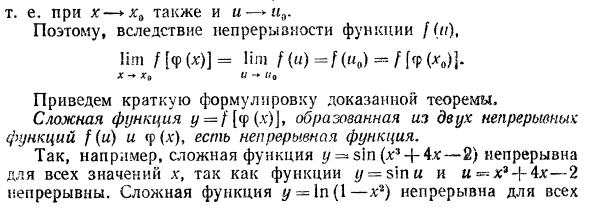

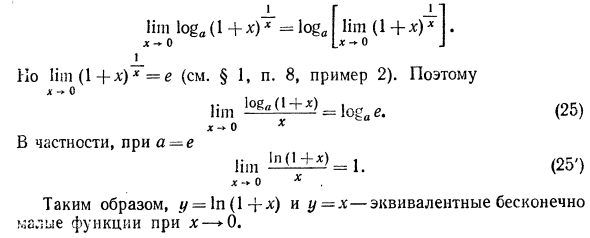









Непрерывные функции
- Непрерывная функция /. Непрерывность функции в определенной точке. Breakpoints Понятие непрерывности функции интуитивно связано с тем, что граф является гладкой линией, которая нигде не прерывается. Изучая график такой функции y — f (x), мы видим, что значения аргумента close соответствуют close. Теорема Депье. Теорема обобщается на любое конечное число членов или факторов. Установить преемственность некоторых основных функций.
Нетрудно показать, что функции от y до x непрерывны во всей области их определения, то есть по всей оси значений. Так функция? / = Cl «(η — положительное целое число) непрерывно по числовой оси как произведение непрерывной функции y = C и y = x. Cx «=> Cxh .. п фактор многочлен y = a0x «4- agxn-1 + … + a _rx + an -Прерывная функция по оси значений в виде суммы непрерывных функций. Кроме того, согласно теореме 1 рациональная функция, являющаяся частным от деления двух многочленов, непрерывна во всех точках, кроме точки исчезновения знаменателя.
Понятно, что постоянная функция y-C непрерывна по оси значений. Людмила Фирмаль
Так, например, функция y = V «‘i непрерывно во всех точках на оси значений при условии, что X я По точкам х-1 и х = 1. В общем, все основные примитивные функции могут оказаться непрерывными для всех значений x, в которых они определены. Введено понятие вашей сложной функции. Если аргумент и функция yf (u) являются функциями новой переменной x, то есть — (p (x), эта функция называется комплексной и y = f \ φ ()] (гл.1, §4 , Стр. 6). Справедлива следующая теорема о непрерывности комплексных функций. Теорема 2. Если функция y = (p (x) продолжается в точке dv, а функция y = f (u) продолжается в точке ua = y (x0), комплексная функция yf [φ ()] является точкой Непрерывный х0. Доказательство. Для доказательства теоремы достаточно установить lim / [<p ()] [
,,)}. Конечно, Разрыв функции u = φ (x), lim f (*) = * f (x0) = «» »
То есть u-> u9 для x- + x0. Следовательно, из-за непрерывности функции {(u) Iim / 1ММ] = lim / ()) = / K) = / f <pM X x0 и u0 Краткое объяснение доказанной теоремы. Комплексная функция y-f [φ (*)], образованная из двух непрерывных функций f (u) и φ (a ′), является непрерывной функцией. Так, например, функция <= sin и u ^ -x2- * 4x — 2 непрерывны, поэтому комплексная функция y sin + 4x — 2) непрерывна для всех значений a-.
| Прямая и плоскость в пространстве | Производная |
| Поверхности второго порядка | Производные высших порядков |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Комплексная функция * / = 1n (1-x1) непрерывна для всех Неравенство 1 — значение jc, удовлетворяющее x *> 0, то есть в интервале (–1, 1). Как мы знаем (гл. Основные базовые функции непрерывны во всех определенных точках, поэтому мы можем получить из теорем 1 и 2 этого раздела. Все основные функции определены Непрерывно во всех точках, принадлежащих домену. Этот важный результат позволяет легко найти предел базовой функции как x- * x0, если функция определена для x = x0. Для этого достаточно рассчитать значение функции в точке х0. lim f (x) = f (lim x) = f (x0). (24) X- * Xb \ xx0 J
Пример 1. Найти лим B ***. L Решения. Поскольку функция непрерывна в точке x =, lim = 58 4 = 51 = 5. L Пример 2. Найти lim logfl (1 + *). я х Решения. Обратите внимание, что при x-> 0 числитель и знаменатель стремятся к нулю одновременно. Это lim loga (1-f x) = х Ah = logc (1 -f 0) 0. Поэтому теорема о дробном пределе здесь не применима. Выполните следующее преобразование: ^ lim 1o ^ (1 + l 🙂 = lim f- • logfl (1-fx)] = lim logu (1 + x 0 x x- »oLA ‘J * -0 Поскольку логарифмическая функция непрерывна, предел может быть достигнут под знаком функции.
В заключение этого пункта мы рассмотрим два ограничения, которые будут необходимы в будущем. Людмила Фирмаль
Горная ложа (l + *) x «logj lim (1 + *) *]. * -О L * -0 J Ho lim (1 + x) * = e (см. § 1, пункт 8, пример 2). так lim M ± £) _ (25) o * В частности, а-е limЯ ± ± £> = 1. (25 ‘) х-х х Следовательно, y = ln (1 + dc) и y = x — бесконечно малые функции, эквивалентные x- * 0.
Пример 3. Нахождение лим ——- • х-0 х ^ Решения. Здесь мы имеем дело с неопределенностью вида -q-. Чтобы найти предел, измените переменную, установив ax — 1 = /. Тогда x- \ oga (t + 1). x-> 0 или как «-0» lim Q ~ 1 = lim i-lim 1 x-o * + i- + o iog «(* + О T 1 1 я — = ln a, lim logfl (* + l) т-0 т Потому что, основываясь на примере 2, lim j «^ = logae. т о ‘ В частности, lim ——- = lne = 1 х * о * То есть x- * 0, y = ex — 1, что является эквивалентной бесконечно малой функцией. 3.
Свойства непрерывных функций на отрезках В этом разделе показаны некоторые свойства непрерывных функций. В этом случае, как правило, мы не проводим доказательств и ограничиваемся формулировками и некоторыми пояснениями. Сначала введите следующие определения: Функция определения y = f (x) называется непрерывной в отрезке [a, b], если она непрерывна во всех внутренних точках Последовательно справа и слева от этого сегмента и на обоих концах сегмента, точки a и b, соответственно .
Теорема 1. Если функция f (x) непрерывна на отрезке [a, b], максимальное и минимальное значения достигаются в этом отрезке. Эта теорема показывает, что в отрезке [a, b] есть точка x19, и значение функциональной диаграммы F (x) в этой точке является наибольшим. Все значения функции на сегменте: / (x) / (,). Аналогично, на сегменте есть точка jc2, где значение функции является наименьшим из всех значений функции на сегменте: f (x) ^ f (x2) (рис. 117).
Замечания. Утверждение теоремы обычно ложно, когда отрезок утверждения теоремы заменяется интервалом (a, b). Так, например, функция y = 5x, которая продолжается в интервале (0, 1), не достигает максимального значения в этом интервале. Он принимает значение, произвольно близкое к 5, но с интервалом (0, 1) нет точки, где функция равна 5 (точка x-1 не принадлежит интервалу). Эта функция не берет минимум на интервале (0, 1). Точно так же вывод теоремы больше не действителен, если функция, определенная в отрезке, терпит разрыв в некоторой точке отрезка.
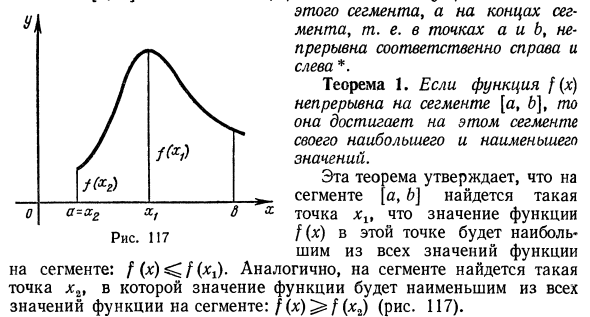
В результате теоремы 1. Если функция f (x) непрерывна на отрезке [a, b], она ограничена этим отрезком. Доказательство. Mit указывает максимальное и минимальное значения функции f (x) на сегменте [a, b] соответственно. Далее, для xy, принадлежащего сегменту, неравенство m <f (x) <M. Пусть C будет максимальным числом чисел | m |, | M тогда | (См. § 1, § 4). Рисунок 118 На фиг. 119 о х в
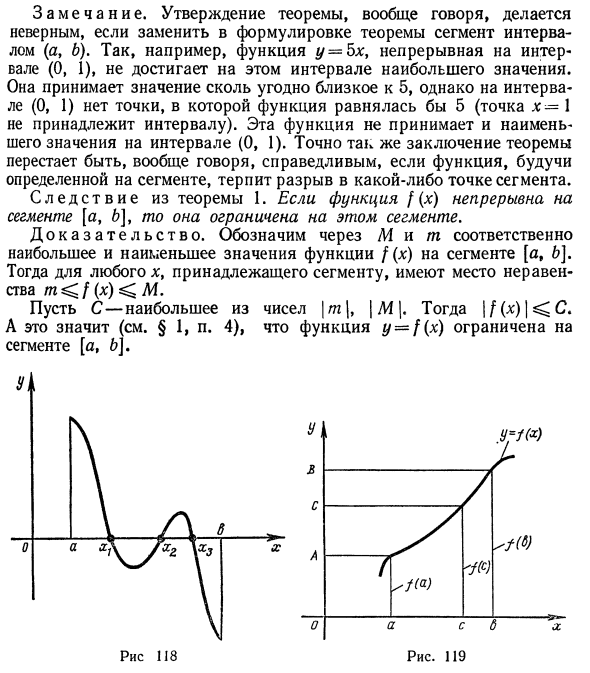
Теорема 2. Если функция y = f (x) непрерывна на отрезке [a> b] и имеет другое значение знака в конце, в этом отрезке есть хотя бы одна точка, где функция равна нулю. Геометрический смысл теоремы заключается в следующем: если точка графика функции y = f (x) t, соответствующая концу отрезка [a, b], находится на другой стороне от оси Ox, то этот график по крайней мере Пересекает ось Ox в одной точке сегмента. Если график является функцией, показанной на диаграмме 118, таких точек три: x19, x2 и x3. Эта теорема допускает следующее обобщение. Теорема 3 (теорема о промежуточном значении). Функция * / = f (x) непрерывна в сегментах [a, b] и f (a) = A, f (b) = B
Для любого числа C между A и B в отрезке есть точка c, так что f (c) = C. Эта теорема геометрически очевидна. Рассмотрим график функции y-f (v) (рис. 119). Пусть f (a) = A, f (b) = B. Линия y = C (C — это любое число, заключенное в A и B), затем пересекает график функции хотя бы в одной точке. Следовательно, непрерывная функция, переходящая из одного значения в другое, обязательно проходит через все промежуточные значения.
Замечания. Утверждения теоремы 2 и 3 неверны, если функция на отрезке имеет хотя бы одну точку останова. Так, например, функция = у положительна для х = \ Отрицательный для х = -1. Однако в сегменте [-1, 1] очки не теряются. Это связано с тем, что сегмент [-1, 1] имеет функцию // = -breakpoint (см. Рис. 115). 4. Концепция обратной функции Давайте начнем с примера. Рассмотрим функцию y = x * t, график которой показан на рисунке. 19. Рассмотрим уравнение y = x3 как уравнение для x. Это уравнение для каждого значения y (-oo <y <H-oo) определяет уникальное значение x: x = \ y y. Геометрически это означает линию, параллельную оси Ox. Пересечь график функции y-x% только в одной точке (см. Рисунок 19).
Следовательно, x можно рассматривать как функцию от y. Функция x = y называется обратной функцией y ^ xr. Далее перейдем к общему случаю. Рассмотрим непрерывную функцию y = f (x), определенную на отрезке или интервале. Если функция такова, что прямая линия, проходящая через 120 единиц параллельно оси Ox, пересекается График существует только в одной точке (рис. 120). То есть уравнение y = f (x) для каждого y
Определите уникальное значение x из диапазона значений функции yf (x) и скажите, что x является функцией y: * = φ (y) у, обратной этой функции tj = f (x) (См. Рис. 120). Очевидно, что если функция x = cp (y), обратная функция — это функция y = f (x). Поэтому обе эти функции называются противоположными друг другу. Эта функция y-f (x) и ее обратное x = t (y) представляют одинаковые отношения между переменными x и y. Однако в первом случае мы рассматриваем x как независимую переменную, а y как функцию. Во втором случае, наоборот, y считается независимой переменной, а x является функцией.
Так же линия Когда независимая переменная x значения функции приближается к точке x0, значение функции y = j (x) приближается к значению функции на бесконечности в точке x0 (рис. 114). Вот строгое определение непрерывности функции. Функция определения y = f (x) называется непрерывной х0, если: 1) Функция определяется точкой x0 и окрестностью, содержащей эту точку. 2) Функция имеет ограничение x-> n-0. 3) Предел функции при x-> x0 равен значению функции в точке x0: Нш / () = / ( о). (22) X- * X, Если функция непрерывна в точке x0, точка x0 называется непрерывной точкой этой функции.
Замечания 1. Уравнение (22) можно записать следующим образом. lim / (*) = f (lim x), (23) X JT, x-r0 Потому что lim x = x0. Уравнение (23) X-X Вы можете перейти к пределу непрерывной функции, пределу ниже знака функции. Замечание 2. Во многих случаях необходимо учитывать непрерывность функции в правой или левой точке x0 (т. Е. Однонаправленная непрерывность). Определите функцию y = f (x) в точке x0. Если lim f (x) -f (x0), функция y-f (x) называется непрерывной. х Х + О Исправить в точке x0, если lim f (x) = f (x0)>, то функция вызывается хх% о Он непрерывен в точке x0 слева. Вот введение в концепцию контрольных точек.
Точка определения x0 принадлежит области функции или ее граничному определению, и, если она не является непрерывной точкой *, она называется разрывом функции y-f (x). Работает как график этой функции y = f (x) и обратной функции x = (p (y), но если ось Ox этой функции является осью независимой переменной, обратная функция x =
0 соответствует двум значениям x \ x = Vy и x = —Vy.
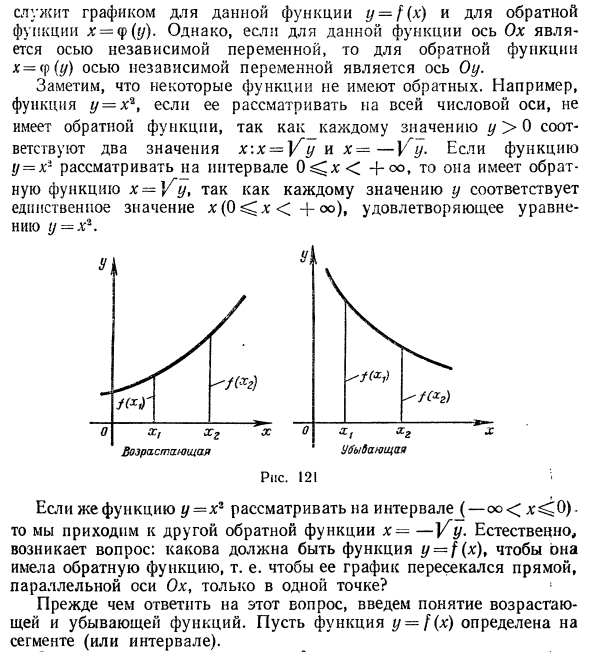
Противоположное верно, если функция tj = xi рассматривается с интервалом 4 °. функция х-уу. Потому что каждому значению y соответствует уникальное значение x: (0 <+ oo). Это удовлетворяет выражению y = xr. X / XG Увеличение слабость Рисунок 121 Если функция y = xr рассматривается в интервале J-oo <* <()). Затем мы приходим к другой обратной функции x = —Yy. Конечно, возникает проблема: должна ли функция y = f (x) 9 иметь обратную функцию, то есть график должен пересекать линию, параллельную оси Ox, только в одной точке? s Прежде чем ответить на этот вопрос, я представлю концепцию увеличения и уменьшения функций. Определите функцию y = f (x) в сегментах (или интервалах).
Функция определения y = f (x) имеет вид f (x2)> f (x ^, если большое значение независимой переменной (из этого сегмента или интервала) соответствует большому значению функции, то есть, если xr> xx ). Функция y = [(x) называется функцией потерь для конкретного сегмента (или интервала), если большое значение независимой переменной соответствует малому значению функции, то есть если xr> xr. Рисунок 121 — график увеличения и уменьшения функции. Например, функции увеличиваются в целом Ось значений; функция y = x2 возрастает с 0 <v, << оо, и уменьшается с -oo <n: <0.
Функция y-f (x), определяемая интервалом (или сегментом), увеличивается или уменьшается только на этом Интервал (или сегмент) называется монотонным с интервалом (или сегментом). На рисунке 121 показано, что каждая линия, параллельная оси Ox, пересекает график монотонной функции в одной точке, то есть каждому значению y соответствует уникальное значение x, поэтому функция yf (x) Вы можете непосредственно видеть, что это обратная функция.
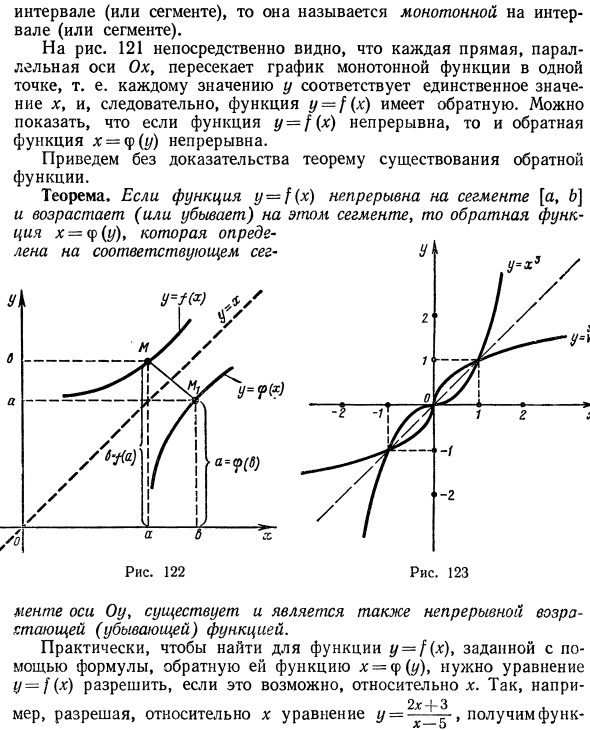
Если функция y = f (x) непрерывна, обратная функция x = µ (y) показана непрерывной. Без доказательства приведем теорему о существовании обратных функций. Теорема: если функция y — f (x) непрерывна в сегменте [a, b] и увеличивается (или уменьшается) в этом сегменте, обратная функция Ось Oy> существует и также является функцией непрерывного увеличения (уменьшения). На практике, чтобы найти обратную функцию x = y (y) функции y = f (x), определенной с помощью формулы, нам необходимо решить формулу y-f (x) относительно x, если это возможно. Так например 2t -4 3 Измерение и решение уравнения y = -r— относительно x дает
х = противоположность этому. у ^ В заключение, вот один важный момент. Функция x: = φ (y) обратна функции y = f (x). Возвращаясь к нормальным обозначениям независимой переменной по x и функции по y, мы можем записать эту обратную функцию в виде (/ = <p (*). Например, обратная функция y = x — это функция x = ] Изменить обозначение переменной, y = j / x. График обратной функции y = cp (x) симметричен относительно графика этой функции y = f (x) относительно биссектрисы координатных углов I и III. В этом легко убедиться, посмотрев на диаграмму. 122. Рисунок 123_
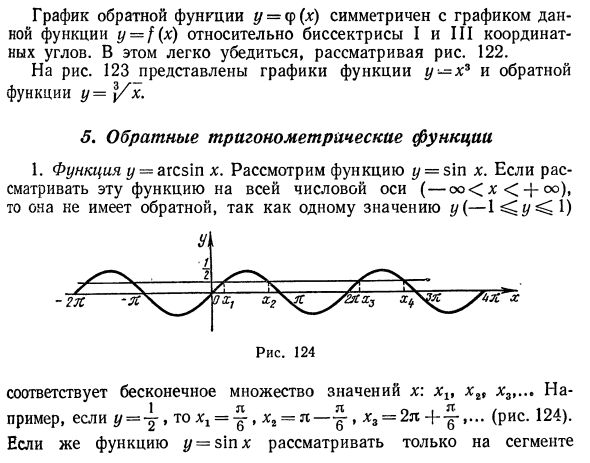
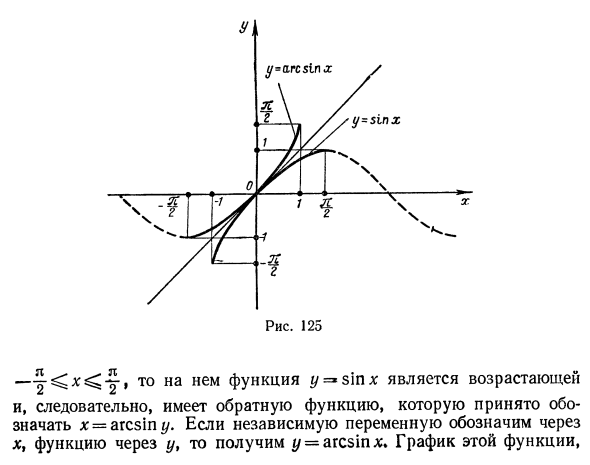
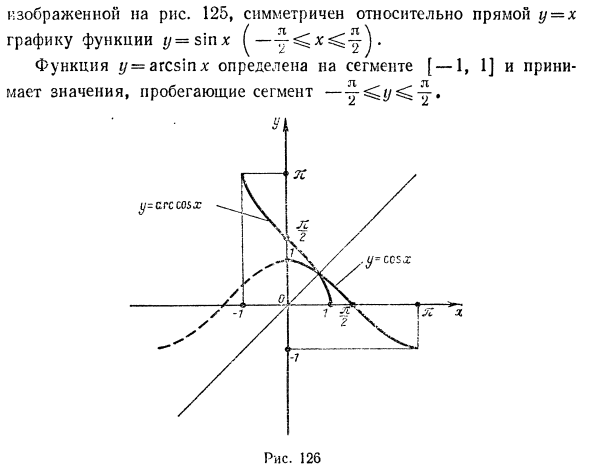
Отображается график функции y-x * и обратной функции y = Yx. 5. Обратные тригонометрические функции 1. Функция y-arcsin x. Рассмотрим функцию r = sin x. Если эта функция рассматривается для всей оси значений (-oo <x <oo), одно значение y (- в J 2л угол Рис. 124 Поддерживает бесконечный набор значений x: xlt xr, Na- Например, когда y = \ * TO * i = 7f и x2 = 71 -% ** 3 = 2π (фиг. 124). Если функция y = s \ nx рассматривается только на сегментах в -Тогда функция y = * sin l: увеличивается Следовательно, она обычно имеет обратную функцию, представленную как x = arcsinr /. Если независимая переменная представлена x, а функция представлена y, то y = arcsinx. График этой функции,
График- ^ из 125, функция y = sinx ^ -y ^ x ^ -m), показанный на рисунке, симметричен относительно линии y = x. Функция y-arcsinx определена в сегменте [-1, 1] Рис. 126 Функция y-arccos x. Функция y = arccos n ‘определяется как обратная функция tj = cos x, где последняя рассматривается на отрезке [0, i]. В этом сегменте функция y = cosx уменьшается. Функция y = arccosx определена в сегменте [-1, 1], и ее значение проходит через сегмент [0, l]. График функции y = arccosx Y показан на рисунке. 126. 3.
Функция y = arctg *. L Функция y = arctgx определяется как обратная функция y-igx. Последнее считается для всех значений х между ними. делать — у и у. На рисунке 127 показан график функции y = -arctg.v. Рисунок 127 Функция y = arclgx определяется целой строкой, и ее значение охватывает интервал Lim arctan x = ~ (см. Рис. 127). 4. Функция y является arcctgA ‘. Функция // = arcctgx определяется как обратная функция r / = ctg x (если это последняя)
Пожалуйста, рассмотрите из интервала (0, л). График функции y-arcctg * показан на рисунке. 127. Функция y = arcctgx определяется во всей числовой строке, iiin arcctg x = i, lim arcctg x = 0 (см. Рис. 127). X- * -Y) X— + CD Функции arcsinx, arccosx, arctg jc и arcctgx называются обратными тригонометрическими функциями. Все они непрерывны при y ^ s’mx, y = cosx, y = txx, y = zigx, что является инверсией непрерывной функции в каждой точке определяющей функции. 6. Экспоненциальные и логарифмические функции Как мы знаем (см. Гл. I, §4, стр.5), функция y = ax называется экспоненциальной функцией (при условии, что основание a, не равное 1, положительно). x y = ax> для любого значения 0.
Таким образом, экспоненциальный граф находится на оси Ox. Если a> 1, функция y = ax увеличивается с уменьшением a <1. График показательной функции показан на рисунке. 23. Если основание -> 1, 23, lim ax = 0 и lim ax- + , как видно. X- * -00 X— + 00 Логарифмическая функция y = \ ogax является инверсией экспоненциальной функции y-ax. График логарифмической функции y = \ ogax показан на рисунке. 24. Как видно из рисунка, функция y-logax определена для всех положительных значений x. Кроме того, если а> 1, lim logax = —a bgax = + oo. x- «0 + 0 DG- + 00 Учитывая базис a-et, что функция y = 1nx противоположна относительно экспоненциальной функции y-ex. В заключение, из определения логарифмической функции как обратной экспоненциальной функции, a ^ x 7. Концепция гиперболической функции
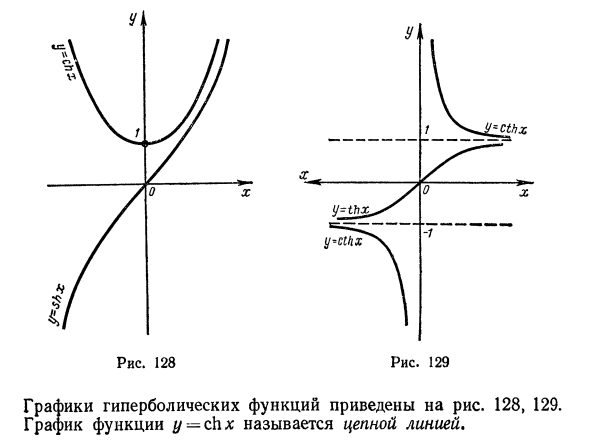
В математике и ее приложениях рассматриваются гиперболические функции: гиперболический синус shx, гиперболический косинус chx, гиперболический тангенс th x, гиперболический котангенс cthx. Эти функции определяются следующими уравнениями: sh * = —2- • chx: = — [hx = = (2b) Где r — основание натурального логарифма. Среди гиперболических функций есть следующие основные зависимости, которые легко проверить с помощью вражеских мулов (26): ch * x — sh8 x-1, = cthx = r (27) ч х * ш к в
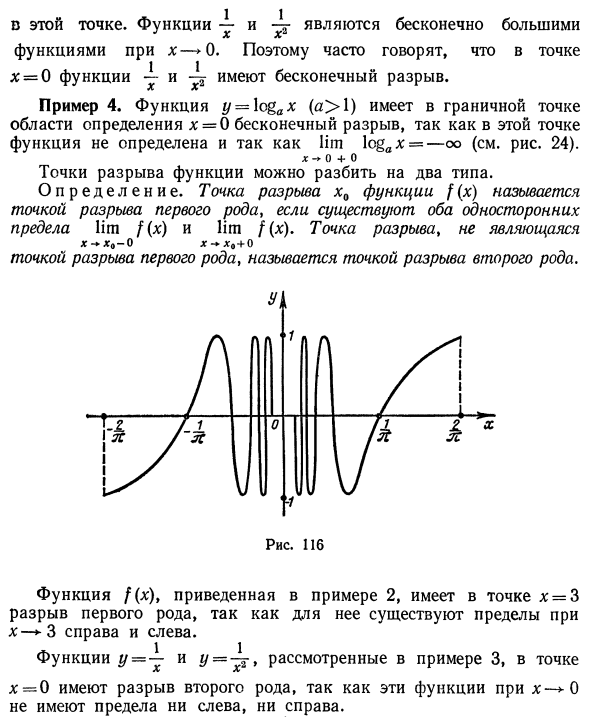
В этом случае, если x = x0, функция называется разрывной. Это тот случай, если функция не определена в точке n0, или если предел функции не существует в x x0, или, наконец, График гиперболической функции показан на рисунке. 128 график функции y-chx называется цепной линией. Функция существует, но не равна значению функции в точке xy: lim / () # / ( •). X- * .r „ Пример 1. Рассмотрим функцию y = 5×3. Докажите, что оно непрерывно в точке x = 2. Для этого точка x = 2 удовлетворяет всем трем условиям, которые являются частью определения непрерывной функции, т.е. 1)
функция находится в точке x — 2 и некоторых ее окрестностях; 2) lim / (Jc) и 3) имеют это ограничение х- + 2 Эквивалентно значению функции в точке x = 2. Функция / (, ) = 5he определена для всей оси значений, поэтому первое условие автоматически выполняется. Кроме того, lim / () = lim Bx’l = 40. так х- + 2 х-2 Второе условие выполнено. Наконец, / (2) = 40 lim f (x) = f (2), * -2 Другими словами, выполняется третье условие, которое определяет непрерывность функции в точке x = 2.
Поэтому функция y = 5×3 непрерывна в точке x-2. Точно так же можно показать, что эта функция непрерывна в любой точке на оси значений. Рис. 1! 5 Пример 2. Рассмотрим функцию f {Y \ -j x— * «, если 0 <x <3; ‘~ \ 3 — x, если 3 <x <4, Пример 2, § 1, пункт 3 показывает. Эта функция определена для всех точек в сегменте [0, 4], а значение при x = 3 равно 0.
(См. График функций на фиг. 109). Однако в точке х-3 ограничения по х-3 отсутствуют, поэтому в функции есть разрыв. Тренажерный зал / (*) = 2 l- удивительно lim / (x) = 0. Обратите внимание, что функция j (x) непрерывна х-3 + 0 За исключением точки х-3 во всех точках отрезка [0, 4] lim f (x) = lim (x-1) = f (0) = -1, * — »0 + 0 x-0 + 0 lim / (*) = lim (3 — a) = / (4) = -1. х-4-0 х 4-0 Пример 3. Функции y = -j и Y- (рис. 115) не определены и поэтому являются разрывными в граничной точке области с определением x = 0.
На данный момент. Функции-и \ являются бесконечно большими функциями, такими как x-> 0. Таким образом, в точке x = 0 функции -4 часто называют бесконечными разрывами. Х х Пример 4. Функция y = \ ogax (a> 1) имеет бесконечный разрыв в граничной точке области определения x = 0. Поскольку функция не определена в этой точке, lim logex: = –∞ (см. Рисунок 24). х о + о Точки останова функции могут быть классифицированы на два типа. Тонкая точка в точке разрыва x0 в функции определения f (x) называется точкой разрыва первого рода, если существуют как односторонние ограничения lim f (x), так и lim / (*). Точка останова x x0-O x- + x0 + 0 Точка останова типа 1 называется точкой останова типа 2. Функция f (x) t, показанная в примере 2, имеет разрыв первого рода при x = 3. Это потому что есть x- * 3 ограничения слева и справа.
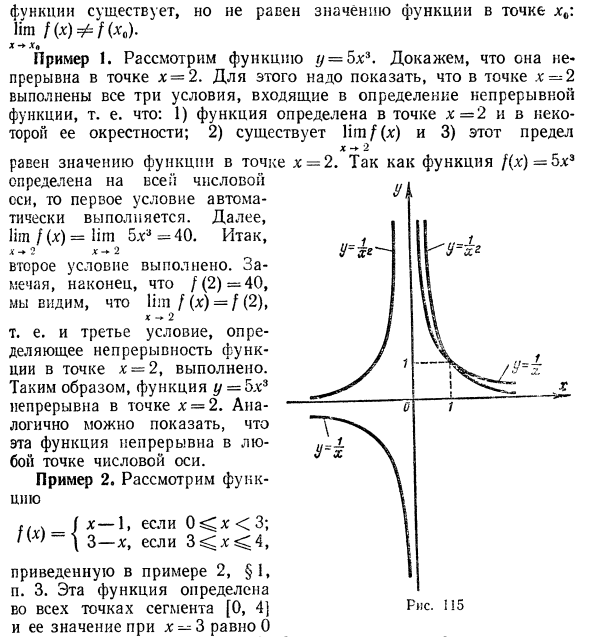
Функции yy, y- \ y являются примером 3, Х Х » х = 0 имеет второй вид разрыва. Это потому, что эти функции как x-►O не имеют ограничений ни с левой, ни с правой стороны. Пример 5. Функция f / = sin — ^ — определена для всех значений x. За исключением х = 0. На этом этапе есть разрыв. Точка x = 0 является вторым видом разрыва. Потому что х — 0 Слева функция sin-, которая колеблется между -1 и +1, не приближается к числовому значению. График показан на рисунке. 116. Пример 6. Функция не определена в точке x = 0. Точка x = 0 является точкой останова типа 1, потому что x—> 0.
Есть ограничения слева и справа. ,. sin * «sin * t urn- = 1, lim- = 1. + 0 * х 0-0 х Если вы определите функцию ^^ с точкой x = 0 и установите / (0) = 1 „, вы получите непрерывную функцию, определенную следующим образом: / () — »Если xΦ0 \ / (0) = 1. Определив функцию с точкой l: = 0, мы закрыли пробел. lim / () = разрывная точка x0 первого рода lim f (x) x- * xo + 0 x-fx0-0 Это называется съемной точкой разрыва. В заключение этого раздела рассмотрим одно свойство функции, которая в какой-то момент непрерывна.
Если функция f (x), непрерывная в точке x0, имеет положительное (отрицательное) значение в точке x0, она остается положительной (отрицательной) во всех точках вблизи точки x0. Конечно, f (x0)> 0. f (x0) — -e> 0. lim f (x) = f (x0) (для непрерывности функции) X- * x0 Точка x0), основываясь на определении предела функции x- * x0 (см. С.167), все точки в интервале (Nt M) (x) -f (x0) \ 0, 0 для всех точек (N, M) из / (*)> интервала. Поэтому функция f (x) положительна вблизи точки x0. 2. Непрерывная работа функции. Непрерывность элементарной функции Если вы выполняете сложение, умножение и деление с помощью непрерывной функции, результатом будет непрерывная функция.
Справедлива следующая теорема. Теорема 1. Если функции φ (χ) и ^ (x) непрерывны в точке xi, их сумма и произведение также непрерывны в точке x0. Кроме случаев Кроме того, для (x0) Φ0 функция продолжается в точке x0. Доказательство. Например, давайте докажем непрерывность произведения f (x). В точке x0 определена функция f (x) = φ (x) • φ (x) и f (* 0) = φ (χ; 0) -φ (x0). Из непрерывности функции при х0: lim φ (*) = φ (x0), Hmφ (x) = φ (x0). применять X- * X0 X- * x0 Предельная теорема о произведении состоит в следующем. lim f (x) = lim [φ (x) -FM] = Пшф (х). limφ (x) = φ (* 0) −φ (x: 0). x- * x9 x- * Xe x-> x0 x- * x0 Таким образом, lim f (x) = f (x0) доказывает непрерывность функции в точке x0. Остальные утверждения также доказаны.

