Оглавление:






Основные положения температур
- Ключевой момент Если температурное поле изменяется со временем, тепловой процесс, который происходит в таких условиях, называется переходным процессом. Нестабильные процессы теплопроводности происходят при охлаждении металлической заготовки, твердом обжиге, изготовлении стекла, обжиге кирпича, нагреве древесины,
резиновой вулканизации и «нагревании мешков с мукой». Теплообмен в нестационарном режиме может быть определен путем нахождения закона флуктуаций температуры и временных потоков во времени и пространстве. F / (*, V> r, m) и Q = φ (x, y, r, m), % Где x, y, r — координаты точки. t- время. Указанная зависимость может быть
найдена из решения дифференциального уравнения теплопроводности Фурье. и начальное распределение температуры в теле. Граничные условия задаются уравнением (Dt / dn) a0B = — («Ast» (/ pov- / medium), (25-2) Где (dt / dn) a0n — градиент
При решении уравнения (25-1) необходимо установить граничные условия Людмила Фирмаль
температуры поверхности. а — коэффициент теплопередачи между жидкой средой и поверхностью твердого тела. Lst-wall теплопроводность; / pov-температура стенки; ^ cpcabI ~ температура окружающей среды. Физические величины ^ C, p считаются постоянными. Температура рассматриваемого тела в начале m = 0 распределяется равномерно. t0-Const Решение уравнений (25-1) и (25-2) с учетом границ и времени дает уравнения для температурного
поля вида t = / (a, X, a, m, l:, y, r, lo> k, 4). (25-3) Уравнение (25-3) показывает, что температура зависит от многих переменных и постоянных параметров, решение — очень сложная математическая задача, и ее невозможно отобразить * в кратком учебнике. , Подробное описание решения доступно в специальном курсе по теплообмену. Поэтому в будущем мы ограничены предоставлением
готовых формул для трех задач о неограниченных пластинах, цилиндрах бесконечной длины и шариках. Анализ уравнения (25-3) показывает, что переменные могут быть сгруппированы в три безразмерных комплекса. ~ = Bi — это число Био. Год выпуска: y- = Fo — число Фурье. Безразмерные координаты. Желаемая функция в виде безразмерной температуры может быть выражена как: Fo.Bi.f). (25-4)
- Неограниченная тарелка ■ Рассмотрите возможность охлаждения плоскопараллельной пластины толщиной. : 6 (/ = 6). Размеры пластины в направлении осей Oy и Og бесконечно малы (рис. 25-1). Пластина очищается с обеих сторон жидкостью или газом с постоянной температурой * ср и коэффициентом теплопередачи.
Значения для обеих поверхностей одинаковы и постоянны. Первоначально пластина имеет постоянную температуру t0 во всех точках, поэтому избыточная температура-> o- * cp также постоянна во всех точках тела. Кроме того, коэффициент Аданы A.st теплопроводности, плотности тела p и его теплоемкости c предполагается постоянным. Коэффициент температуропроводности
a определяется уравнением a = Mer. Поскольку пластина не ограничена ни по высоте, ни по ширине, дифференциальное уравнение принимает вид: дх * ‘ Граничное условие x = ± b (- \ = ± abst \ dx) x = ± 6 А, (М = 0 начальное условие th = Рисунок 25-1 * Ниже Φ понимается как избыточная температура тела в пересчете на температуру окружающей среды, фут = * гела / Сред- Температура
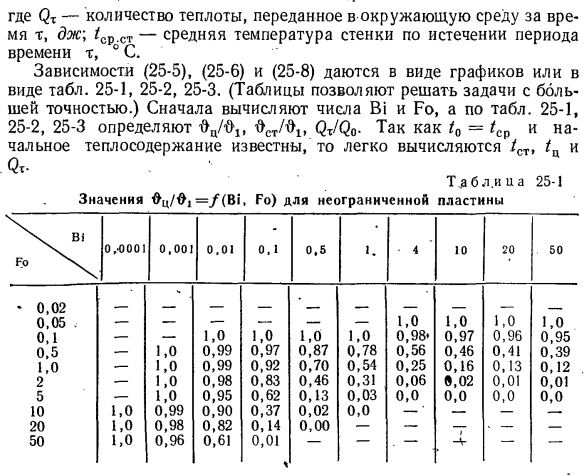
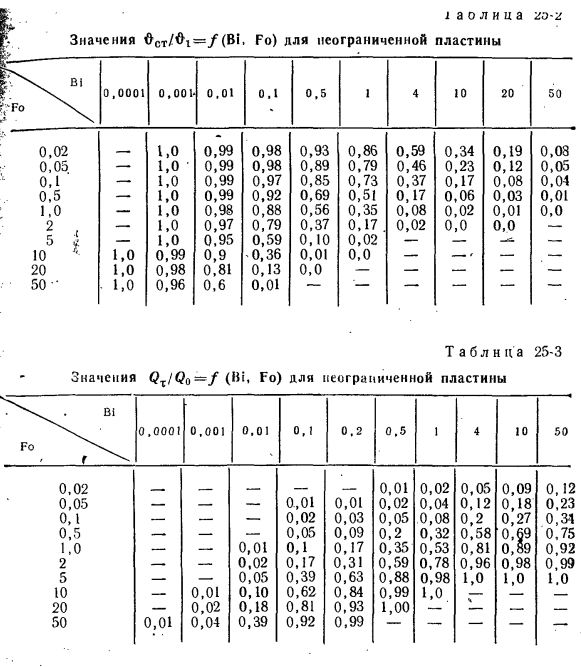
поверхности стены и ее центральной плоскости определяется из соотношения ^ = ^ fl) = / (Bi> Fo). (25-5) к — tcp \ LST I *) Б и поверхности пластины является постоянным значением (если x = 0 xll = 0, l: = b xll = 1), поэтому ее нет в уравнении (25-5). w-‘op = / i (Bif Fo) {25 6) VI * 0,5 .- 1,0 0,99 0,97 0,87 0,78 0,56 0,46 0,41 0,39 ^ «1,0 ™ .- 1,0 0,99 0,92 0,70 0,54 0,25 0,16 0,13 0,12 2 .- 1,0 0,98 0,83 0,46 0,31 0,06 дюйма, 02 0,01 0,01 5 .- 1,0 0,95 0,62 0,13 0,03 0,0 0,0 0,0 0,0 10 1,0 0,99 0,90 0,37 0,02 0,0 -‘— 20 1,0 0,98 0,82 0,14 0,00 $ 50 1,0 0,96 0,61 0,01 ч до -V i OCT / Ol = / (Bi, Fo)
езразмерная координата xll центральной плоскости Людмила Фирмаль
Неограниченное значение пластины 0,0001 0,001-0,01 0,1 0,5 1 4 10 20 50 по 0,19 0,12 0,08 0,03 0,01 0,0 0,59 0,46 0,37 0,17 0,08 0,02 0,93 0,89 0,85 0,69 0,56 0,37 0,10 0,01 0,0 0,86 0,79 0,73 0,51 0,35 0,17 0,02 0,0 0,34 0,23 0,17 0,06 0,02 0,0 0,98 0,98 0,97 0,92 0,88 0,79 0,59 • 0,36 0,13 0,01 0,99 0,99 0,99 0,99 0,98 0,97 0,95 0,9 0,81 0,6 1,0 1,0 • 1,0 1,0 1,0 1,0 1,0 0,99 0,98 0,96 0,02 0,05 OD 0,5 1,0 2 5 10 20 50 » 1,0 1,0 1,0 Таблица 25-3 Значение C? T / Oo = / Fo) A- ™ неограниченная пластина , B1 » 0,0001 0,001 0,01 0,1 0,2 0,5 1 4 10 50 Fo е 0,01 0,02 0,05 0,09 0,12 _ -0,01 0,01 0,02 0,04 0,12 0,18 0,23 -0,02 0,03 0,05 0,08 0,2 0,27 0,3-1 . -0,05 0,09 0,2 0,32 0,58 0,69 0,75 _ 0,01 0,1 0,17 0,35 0,53 0,81 0,89 0,92 , _ 0,02 0,17 0,31 0,59 0,78 0,96 0,98 0,99 -_ 0,05 0,39 0,63 0,88 0,98 1,0 1,0 1,0 _ 0,01 0,10 0,62 0,84 0,99 1,0. — _ 0,02 0,18 0,81 0,93 1,00 — 0,01 0,04 0,39 0,92 0,99 0,02 0,05 0,1 0,5 1,0 2 5 10 20 50
Смотрите также:
Решение задач по термодинамике
| Передача теплоты через шаровую стенку | Цилиндр бесконечной длины |
| Интенсификация теплопередачи | Регулярный режим теплопроводности |

