Оглавление:


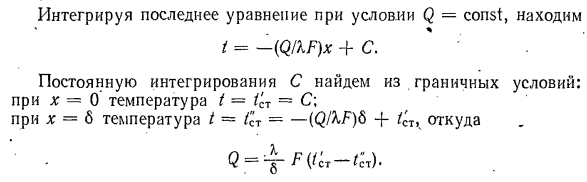

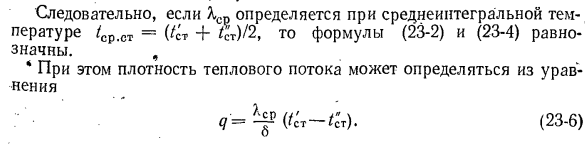


Теплопроводность через однослойную плоскую стенку
- Теплопроводность через единственную плоскую стенку Уравнение дифференциальной теплоты позволяет определять температуру как функцию времени и определять координаты в любой точке поля. , «» В определенных случаях необходимо приложить необходимые граничные условия. Наиболее распространенный случай — рассмотреть теплопроводность через единую плоскую стенку. Его
длина и ширина бесконечно больше толщины 6 (Рисунок 23-1). Стенка имеет одинаковую толщину во всех частях, а температура поверхности / с и / с поддерживается постоянной. То есть они являются изотермическими поверхностями. Температура изменяется только в направлении, перпендикулярном плоскости стены. Это считается осью X. Теплопроводность X постоянна по всей стене. В
устойчивом тепловом режиме температура в любой точке объекта постояиальной теплоты после снижения температуропроводности принимает вид: (DH / dx2) + (dH! Dy2) + • (d2t / dz2) = 0 Однако при принятых условиях первая и вторая производные от / для y и z также равны нулю. dfldy-dildz = 0 и dltldif = d2 // dg2 = 0, Таким образом, уравнение теплопроводности можно
нна и не зависит от времени. То есть d // dt = 0. После этого уравнение дифференц Людмила Фирмаль
записать в виде d2t / dx2 = 0. * (23-1) Интегральное уравнение (23-1), dt / dx-const = A. После квадратичного интегрирования получается I t = Ax + B. Я Если теплопроводность постоянна, это линейное уравнение. В результате закон изменения температуры при прохождении тепла через плоскую стенку оказывается линейным. Найти константы интегрирования A и B. Рисунок 23-1 * = 0, температура t = B \ x = 6,
температура t = / st = Ad + / s’t , A = (Gst-t’c t) / 6 = Получите плотность теплового потока из уравнения (22-7): q = -X ((dt / dn) = -X (<Wk) = -H (gT-k) / «. или ? = (23-2) Если вы знаете удельный тепловой поток, вы можете рассчитать общее количество тепла, которое проходит через стенку F в течение времени t Q = ~ F (tc, -t, ) x. «(23-3) о Количество тепла, передаваемого теплопроводностью через плоскую стенку,
прямо пропорционально теплопроводности стенки X ее области F, временному интервалу t, разности температур (/ ct-t) на наружной поверхности стенки, Он обратно пропорционален толщине стенки 6. От абсолютного значения температуры и разности между ними / st- = температура называется головкой. Полученная формула (23-2) эффективна при постоянной теплопроводности. Фактически
- теплопроводность реального объекта зависит от температуры, а закон изменения температуры представлен кривой. На практике закон изменения температуры считается линейным, если теплопроводность не сильно зависит от температуры. Уравнение (23-2) можно получить непосредственно из закона Фурье (22-6), предполагая, что температура изменяется только в направлении оси x. Q = —XF (dtidx)% Разделение переменных dt = — {QiXF) dx.
Интегрируя последнее уравнение при условии Q = const, t = — (Q / kF) x + C Найти постоянную интегрирования С. Граничное условие: l: = 0 температура t = t’CT = С; температура t- / c’t = — (QAF) 6 + откуда при x = 6 Вводит коррекцию зависимости от / в уравнении (23-2). * Предполагается, что эта зависимость является линейной. Х = Х, (1 + S). ‘9 (а) В этом случае подстановка значения из уравнения (а) вместо X в
уравнение Фурье приводит к: q = -X (t) £ = -X0 (+ bi) — £. (6) Ад: ад: Если вы разделяете и объединяетy x = 0 i = tiT и (g) Для x = 6 t = / cm и <6 =. + ^) + C. (e) \ Вычитая первое (d) из второго уравнения (e) (TCR-PG). — (23-4) Полученное уравнение (23-4) можно использовать для определения плотности теплового потока с использованием переменного коэффициента теплопроводности. В этом уравнении
е переменные, qx ^ -X ^ t + ^ + C. ^ (с) Если для переменной есть граничное значение: y Людмила Фирмаль
фактор , ^ l + ftizJJa) Является средней интегральной величиной теплопроводности. В уравнении (23-2) предполагалось, что X является постоянным и равно среднему значению X (.v. Таким образом, при сравнении уравнений (23-2) и (23-4), , (23-5) эй d = T 1 / ст + / ст Таким образом, если Yaqr определяется средней интегрированной температурой / avrst = (/ st + / st) / 2, уравнения (23-2) и (23-4) эквивалентны. Вы есть * В этом случае плотность теплового потока
можно определить по формуле q = ^ f (золото-GG). (23-6) Уравнение для кривой температуры стенки может быть получено путем решения квадратного уравнения (c) для t и подстановки значения C из уравнения (g). Из этого уравнения видно, что температура внутри стены изменяется. Это изогнуто. Если коэффициент b отрицателен, кривая будет смотреть вниз из-за выпуклости. Если б положительный, он будет набухать.
Смотрите также:
Решение задач по термодинамике
| Дифференциальное уравнение теплопроводности | Теплопроводность через многослойную плоскую стенку |
| Краевые условия | Теплопроводность через многослойную цилиндрическую стенку |

