Оглавление:

Теплотехника (нем. Wärmetechnik) — общетехническая дисциплина, изучающая методы получения, преобразования, передачи и использования теплоты, а также принцип действия и конструктивные особенности тепло- и парогенераторов тепловых машин, агрегатов и устройств. wikipedia.org/wiki/Теплотехника
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в теплотехнику
Теплотехника представляет собой науку, которая изучает законы распространения и передачи теплоты между телами. Вместе с термодинамикой учение о теплообмене составляет теоретические основы теплотехники.
Различают три вида теплообмена: теплопроводность (или кондук-ция), конвекция и тепловое излучение. Теплопроводностью называется перенос теплоты, возникающий при непосредственном соприкосновении между частицами тела.
В жидкостях наряду с теплопроводностью теплота может распространяться также путем перемещения и перемешивания между собой более или менее нагретых частиц самой жидкости. Такой вид распространения теплоты называется конвекцией. В целом явление передачи теплоты при соприкосновении стенки с жидкостью путем теплопроводности и дальнейшее распространение ее в жидкости за счет конвекции (а также процесс, протекающий в обратном направлении) называется конвективным теплообменом, или теплоотдачей.
Тепловым излучением, или лучеиспусканием, называется перенос энергии в виде электромагнитных волн между двумя взаимно излучающими поверхностями. При этом происходит двойное превращение энергии: тепловой энергии в лучистую на поверхности тела, излучающего теплоту, и лучистой энергии в тепловую на поверхности тела, поглощающего лучистую теплоту.
Частные процессы переноса теплоты
Частные процессы переноса теплоты — теплопроводность, конвекция и лучеиспускание обычно происходят одновременно. Например, в топочных устройствах различных технологических установок конвективный перенос теплоты сопровождается тепловым излучением. В этом случае процесс переноса теплоты называется сложным теплообменом.
В теплообменных аппаратах, как правило, происходят одновременно различные виды теплообмена. Например, в паровом котле теплота передается от продуктов сгорания топлива к стенкам кипятильных труб путем излучения и конвекции, через металл стенок труб теплота распространяется путем теплопроводности, и далее осуществляется процесс теплоотдачи кипящей воде или пару. Такой процесс переноса теплоты от греющей среды через стенку к нагреваемой среде называется теплопередачей.
Необходимо отметить, что в тепловых установках, используемых в производстве строительных материалов и изделий, процессы теплообмена являются решающими, так как интенсивность и качество тепловой обработки строительных изделий в значительной мере зависят от правильной работы теплоиспользующей аппаратуры. Очень важно при организации теплообмена в промышленных условиях обеспечить равномерность тепловой обработки во всем объеме камеры или на отдельных
участках непрерывно действующих установок. В противном случае в общей массе обработанной продукции будет содержаться как перегретый, так и недогретый материал. При этом нужно иметь в виду, что тепловая обработка многих строительных изделий сопровождается сложными физико-химическими процессами экзо- или эндотермического характера, учет которых в расчете теплообмена обязателен.
Известно, что процесс распространения теплоты в пространстве неразрывно связан с распределением температуры в нем. Совокупность значений температуры в каждый момент времени для всех точек рассматриваемого пространства называется температурным полем.
Математически оно выражается уравнением 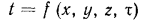 , где, x, у, z — координаты точки, а
, где, x, у, z — координаты точки, а 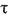 — время. Если температура во времени не меняется, то поле называется установившимся, или стационарным. Если температура зависит от времени, поле называется неустановившимся, а протекающие в таких условиях тепловые процессы — нестационарными, например нагревание или охлаждение тел.
— время. Если температура во времени не меняется, то поле называется установившимся, или стационарным. Если температура зависит от времени, поле называется неустановившимся, а протекающие в таких условиях тепловые процессы — нестационарными, например нагревание или охлаждение тел.
Температурное поле может быть функцией трех, двух и одной координаты. Соответственно оно называется трех, двух- и одномерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля t=f(x). Все точки пространства, имеющие одинаковую температуру, образуют изотермическую поверхность.
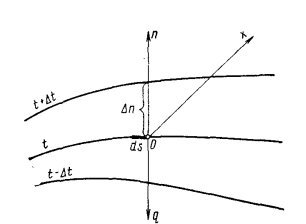
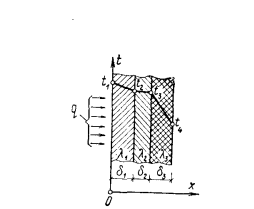
Естественно, что изменение температуры в теле может наблюдаться лишь в направлениях, пересекающих изотермические поверхности (например, направление х, (рис. 13.1). При этом наиболее резкое изменение получается в направлении нормали n к изотермическим поверхностям. Предел отношения изменения температуры 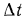 к расстоянию между изотермами по нормали
к расстоянию между изотермами по нормали 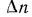 при условии, что
при условии, что 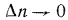 , называется температурным градиентом, т.е.
, называется температурным градиентом, т.е.
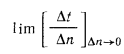
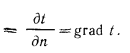
Частная производная применена здесь потому, что в общем случае температура может изменяться не только в пространстве, но и во времени (при нестационарном режиме).
Температурный градиент
Температурный градиент — это вектор с положительным знаком при возрастании температуры и с отрицательным при ее падении. Градиент температуры численно равен производной температуры по нормали.
Количество переносимой теплоты в единицу времени называют тепловым потоком Q, который измеряется вДж/с (Вт). Тепловой поток, отнесенный в единице поверхности тела, называют по верх постной плотностью теплового потока (или просто плотностью теп-
лового потока) q Q/S, которая измеряется в 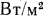
тока
Величина q является вектором, направление которого противоположно направлению градиента температуры, так как тепловая энергия самостоятельно распространяется всегда только в сторону убывания температуры (см. рис. 13.1).
Исследуя явления теплопроводности в твердых телах, Фурье установил, что тепловая мощность, передаваемая теплопроводностью, пропорциональна градиенту температуры и площади сечения, перпендикулярного направлению теплового потока, т. е.
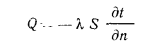
или
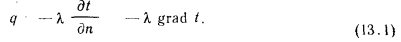
Множитель пропорциональности 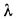 , входящий в это уравнение, характеризует способность вещества, из которою состоит рассматриваемое тело, проводить теплоту и называется коэффициентом теплопроводности, или просто теплопроводностью. Из уравнения (13.1), которое является математическим выражением основного закона распространения теплоты путем теплопроводности (закон Фурье), следует, что теплопроводность
, входящий в это уравнение, характеризует способность вещества, из которою состоит рассматриваемое тело, проводить теплоту и называется коэффициентом теплопроводности, или просто теплопроводностью. Из уравнения (13.1), которое является математическим выражением основного закона распространения теплоты путем теплопроводности (закон Фурье), следует, что теплопроводность 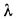 ,
, 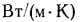 , определяет мощность теплового потока, проходящего через 1
, определяет мощность теплового потока, проходящего через 1 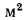 поверхности при градиенте температуры 1 К/м.
поверхности при градиенте температуры 1 К/м.
Возможно эта страница вам будет полезна:
| Решение задач по теплотехнике |
Для различных тел теплопроводность имеет определенное значение и зависит от структуры, плотности, влажности, давления и температуры веществ этих тел. Точные значения 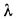 определяют на основе специальных лабораторных опытов. При технических расчетах обычно используют ориентировочные значения теплопроводности
определяют на основе специальных лабораторных опытов. При технических расчетах обычно используют ориентировочные значения теплопроводности 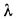 ,
, 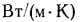

Таким образом, наиболее высокая теплопроводность у металлов, значительно ниже у неметаллических строительных материалов и самые низкие значения у пористых материалов, применяемых специально для тепловой изоляции. У теплоизоляционных материалов 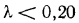 Вт/(м • К) .
Вт/(м • К) .
У большинства металлов с повышением температуры теплопроводность убывает. Содержание примесей в металлах резко снижает их теплопроводность. Например, для стали при 0,1% углерода 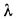 =53, а при 1% углерода
=53, а при 1% углерода 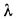 = 39
= 39 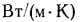 . Для строительных и теплоизоляционных материалов теплопроводность возрастает с увеличением температуры (исключение составляют магнезитовые огнеупоры). Зависимость
. Для строительных и теплоизоляционных материалов теплопроводность возрастает с увеличением температуры (исключение составляют магнезитовые огнеупоры). Зависимость 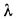 от температуры для этих материалов может быть выражена равенством
от температуры для этих материалов может быть выражена равенством
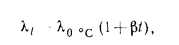
где 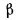 — температурный коэффициент, представляющий собой приращение
— температурный коэффициент, представляющий собой приращение 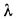 материала при повышении его температуры на
материала при повышении его температуры на 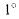 .
.
У различных строительных материалов в интервале температур 0—100° С 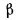 = 0,0025. Для капельных жидкостей с повышением температуры теплопроводность убывает. Исключение составляют лишь вода и глицерин.
= 0,0025. Для капельных жидкостей с повышением температуры теплопроводность убывает. Исключение составляют лишь вода и глицерин.
У газов с повышением температуры теплопроводность возрастает и практически не зависит от давления, за исключением очень высоких (более 200МПа) и очень низких (менее 0,003 МПа) давлений. На теплопроводность влияют общая пористость материала, размер и степень замкнутости пор.
Для пористых материалов теплопроводность находится в обратной зависимости от их общей пористости и в прямой— от размеров пор. Это объясняется увеличением передачи теплоты конвекцией и излучением в общем процессе теплообмена пористого материала и свидетельствует о том, что теплоизоляционные материалы, используемые при высоких температурах, должны иметь мелкопористое строение.
Поры, сообщающиеся между собой и с поверхностью материала, создают более благоприятные условия для увлажнения материала и тем самым для увеличения его теплопроводности, поэтому теплоизоляционные материалы должны иметь по возможности замкнутые поры.
Для пористых материалов 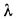 является условной величиной, так как наличие пор в материале не позволяет рассматривать его как сплошное тело. Поэтому
является условной величиной, так как наличие пор в материале не позволяет рассматривать его как сплошное тело. Поэтому 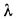 пористых материалов представляет собой теплопроводность некоторого однородного тела, через которое при одинаковых форме, размерах и температурах на границе его поверхности с окружающей средой передаётся та же тепловая мощность, что и через пористое тело.
пористых материалов представляет собой теплопроводность некоторого однородного тела, через которое при одинаковых форме, размерах и температурах на границе его поверхности с окружающей средой передаётся та же тепловая мощность, что и через пористое тело.
Материалы с большей плотностью, как правило, обладают большей теплопроводностью, однако нужно иметь в виду, что теплопроводные свойства материала зависят не только от объема воздуха, заключенного в порах, но главным образом от равномерного распределения воздуха в пористом материале.
С этой точки зрения крупнопористый материал будет менее эффективным теплоизолятором, чем мелкопористый материал с той же плотностью. Среди строительных материалов встречаются такие, которые, имея меньшую плотность, обладают большей теплопро-
водностью, чем материалы с большей плотностью. Примерами могут служить минеральная вата, торфяная крошка, употребляемая в качестве теплоизоляционного сыпучего материала, и др. В частности, у минеральной ваты при плотности около 125 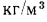 теплопроводность наименьшая.
теплопроводность наименьшая.
При меньшей плотности теплопроводность возрастает в результате увеличения передачи теплоты конвекцией в порах вследствие меньшего уплотнения ваты.
Теплопроводность строительных материалов
Теплопроводность строительных материалов резко возрастает при их увлажнении, гак как значительно отличаются теплопроводности воздуха и воды: теплопроводность воздуха в порах материала 0,025— 0,028, а воды 0,55 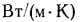 ), т. е. почти в 20 раз больше, чем воздуха. Материал становится еще более теплопроводным, если влага, находящаяся в его порах, замерзает, так как теплопроводность льда равна 2,5
), т. е. почти в 20 раз больше, чем воздуха. Материал становится еще более теплопроводным, если влага, находящаяся в его порах, замерзает, так как теплопроводность льда равна 2,5 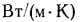 , т. е. примерно в 4 раза выше, чем у воды, и в 80 раз выше, чем у воздуха.
, т. е. примерно в 4 раза выше, чем у воды, и в 80 раз выше, чем у воздуха.
Повышение теплопроводности влажных материалов обусловливается также увеличением контактирующих поверхностей частиц основного вещества материала. Это приводит к тому, что теплопроводность влажного материала значительно выше, чем сухого и воды в отдельности.
Например, для сухого кирпича 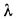 равна 0,35, для воды 0,55, а для влажного кирпича 1
равна 0,35, для воды 0,55, а для влажного кирпича 1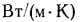 . Поэтому строительные и особенно теплоизоляционные материалы необходимо предохранять от увлажнения, иначе сильно снижаются их теплозащитные свойства.
. Поэтому строительные и особенно теплоизоляционные материалы необходимо предохранять от увлажнения, иначе сильно снижаются их теплозащитные свойства.
Для анизотропных материалов, которые имеют неодинаковую структуру в различных направлениях (древесина, волокнистые и прессованные материалы, кристаллы), теплопроводность зависит от направления теплового потока. Например, у сосновой древесины при направлении теплового потока параллельно направлению волокон 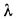 увеличивается вдвое по сравнению с теплопроводностью при направлении теплового потока перпендикулярно волокнам.
увеличивается вдвое по сравнению с теплопроводностью при направлении теплового потока перпендикулярно волокнам.
- Это объясняется тем, что при направлении, перпендикулярном волокнам, тепловому потоку приходится пересекать большое количество воздушных зазоров, находящихся как внутри волокон древесины, так и между ними и оказывающих сопротивление прохождению теплоты. При направлении теплового потока параллельно волокнам влияние воздуха, заключенного в древесине,, будет значительно меньше.
Расчетные формулы при стационарной теплопроводности
Рассмотрим формулы, по которым можно рассчитать количество-теплоты, передаваемой путем теплопроводности через стенки различной конфигурации (плоскую, цилиндрическую; сферическую), и установим для них уравнения температурных полей.
Однородная плоская стенка. Рассмотрим явление теплопроводности в однородной плоской стенке толщиной 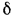 (рис. 13.2). Теплопроводность материала стенки
(рис. 13.2). Теплопроводность материала стенки 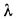 , и пусть на поверхностях стенки поддерживаются постоянные температуры
, и пусть на поверхностях стенки поддерживаются постоянные температуры 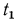 и
и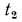 (режим стационарный), причем температурное поле одномерно и меняется только в направлении оси х. Внутренние источники теплоты в стенке отсутствуют. На основа нии уравнения (13.1) для бесконечно тонкого слоя стенки dx взятого на расстоянии от поверхности, будем иметь:
(режим стационарный), причем температурное поле одномерно и меняется только в направлении оси х. Внутренние источники теплоты в стенке отсутствуют. На основа нии уравнения (13.1) для бесконечно тонкого слоя стенки dx взятого на расстоянии от поверхности, будем иметь:
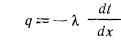 или
или 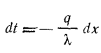 и
и 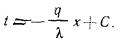
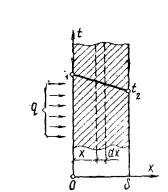
Постоянная интегрирования С определяется из граничных условий: при 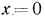
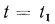 ,
,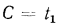 при
при 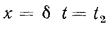
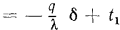 , откуда определяют плотность теплового потока
, откуда определяют плотность теплового потока
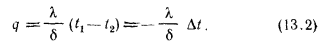
Разность температур 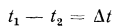 называется температурным напором. Отношение
называется температурным напором. Отношение 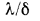
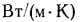 , называется тепловой проводимостью стенки, показывающей, какое количество теплоты проводит 1
, называется тепловой проводимостью стенки, показывающей, какое количество теплоты проводит 1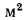 стенки за единицу времени при температурном напоре, равном одному градусу. Обратная величина тепловой проводимости
стенки за единицу времени при температурном напоре, равном одному градусу. Обратная величина тепловой проводимости 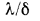
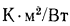 , называется
, называется
термическим сопротивлением стенки, которое определяет падение температуры при прохождении через стенку теплового потока плотностью, равной единице. Подобное название 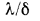 обусловлено тем, что формула (13.2), написанная в виде
обусловлено тем, что формула (13.2), написанная в виде 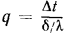 аналогична по форме закону Ома для постоянного тока, и отношение
аналогична по форме закону Ома для постоянного тока, и отношение 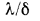 , соответствующее омическому сопротивлению в формуле закона Ома, называют термическим сопротивлением теплопроводности.
, соответствующее омическому сопротивлению в формуле закона Ома, называют термическим сопротивлением теплопроводности.
Если в выражение 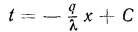 подставить значения
подставить значения 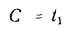 и
и 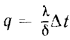 , то получим уравнение температурной кривой
, то получим уравнение температурной кривой

Уравнение (13.3) показывает, что при постоянном значении 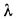 внутри однородной плоской стенки температура изменяется по закону прямой линии. В действительности теплопроводность зависит от температуры, поэтому температура изменяется не по прямой, а по кривой.
внутри однородной плоской стенки температура изменяется по закону прямой линии. В действительности теплопроводность зависит от температуры, поэтому температура изменяется не по прямой, а по кривой.
Зная по уравнению (13.2) величину q, легко определить и общее количество теплоты Q, переданное через плоскую стенку с площадью поверхности S в течение времени 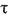 :
:

Многослойная плоская стенка. В строительстве наиболее распространенный тип ограждения — многослойные конструкции. Например, стены жилых домов на основном кирпичном слое с одной стороны имеют внутреннюю штукатурку, а с другой — внешнюю облицовку. Обмуровка топок и печей, используемых в промышленности строительных материалов, также обычно состоит из нескольких слоев: слоя огнеупорной кладки, слоя обычного кирпича и слоя тепловой изоляции.
Рассмотрим плоскую стенку, составленную из нескольких например трех, разнородных, плотно прилегающих друг к другу слоев (рис. 13.3). Толщины слоев и соответствующие значения теплопроводности составляют 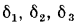 и
и 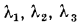 .
.
Кроме того, заданы температуры наружных поверхностей стенки 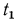 и
и 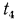 . Соприкасающиеся поверхности слоев имеют температуры
. Соприкасающиеся поверхности слоев имеют температуры 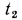 и
и 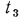 , но значения их неизвестны Поскольку мы рассматриваем стационарный режим, то плотность теплового потока q , проходящего через каждый слой стенки, по величине одинакова. На основании формулы (13.2) для каждого слоя можно написать:
, но значения их неизвестны Поскольку мы рассматриваем стационарный режим, то плотность теплового потока q , проходящего через каждый слой стенки, по величине одинакова. На основании формулы (13.2) для каждого слоя можно написать:
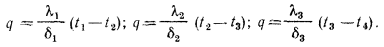
Исходя из написанных уравнений, находим изменения температуры в каждом слое и, складывая их, получим температурный напор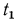 —
— 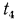 =
=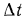 т. е.
т. е.
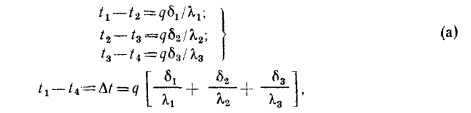
откуда
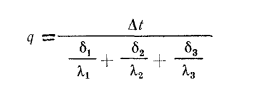
По аналогии для n-слойной стенки расчетную формулу можно написать так:

Из полученного уравнения следует, что общее термическое сопротивление многослойной стенки равно сумме частных термических сопротивлений.
Если значение теплового потока, определенного по формуле (13.5), подставить в равенство (а), можно найти неизвестные температуры 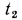 и
и 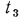 :
:
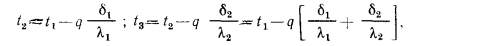
или
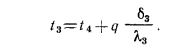
Внутри каждого слоя температура изменяется по закону прямой линии (при 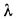 = const), а для многослойной стенки она представляет собой ломаную линию (см. рис. 13.3), так как каждый слой стенки имеет свое значение
= const), а для многослойной стенки она представляет собой ломаную линию (см. рис. 13.3), так как каждый слой стенки имеет свое значение 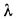 .
.
Возможно эта страница вам будет полезна:
| Методические указания по теплотехнике |
В некоторых случаях многослойную стенку рассчитывают как однослойную однородную стенку с такой же толщиной  , т.е.
, т.е. 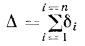 .
.
При этом в расчет вводится так называемая эквивалентная теплопроводность 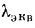 , определяемая из соотношения
, определяемая из соотношения
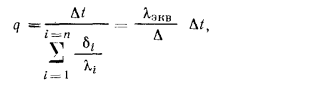
откуда

Однослойная цилиндрическая стенка
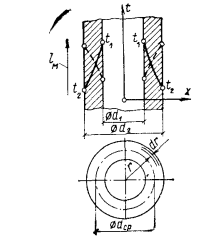
Рассмотрим однородную цилиндрическую стенку (трубу) длиной l с внутренним диаметром 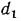 и наружным
и наружным 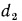 . Теплопроводность материала имеет постоянное значение и равна
. Теплопроводность материала имеет постоянное значение и равна 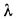 . На внутренней и наружной поверхностях трубы поддерживаются постоянные температуры
. На внутренней и наружной поверхностях трубы поддерживаются постоянные температуры 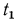 и
и 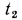 (рис. 13.4), причем
(рис. 13.4), причем 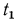
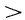
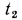 . Температурное поле считаем одномерным, т. е. температура меняется только в радиальном направлении. В этом случае изотермические поверхности будут представлять собой цилиндрические поверхности, имеющие общую ось с трубой. Внутри рассматриваемой стенки выделим кольцевой слой радиусом r и толщиной dr. Тогда, по закону Фурье, количество теплоты, проходящей через этот слой за единицу времени,
. Температурное поле считаем одномерным, т. е. температура меняется только в радиальном направлении. В этом случае изотермические поверхности будут представлять собой цилиндрические поверхности, имеющие общую ось с трубой. Внутри рассматриваемой стенки выделим кольцевой слой радиусом r и толщиной dr. Тогда, по закону Фурье, количество теплоты, проходящей через этот слой за единицу времени,
равно:
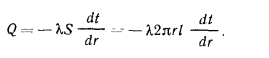
Разделяя переменные и интегрируя, получим:
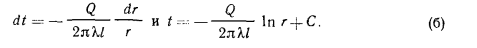
Используя граничные условия, находим: при 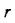
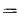
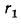
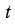
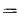
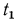 и при
и при 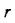
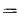
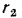
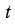
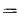
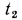 .
.
Тогда:
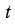
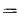
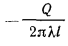
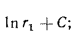
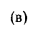
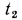
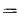
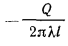
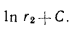
Вычитая из равенства (в) равенство (г), получим:
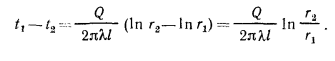
или
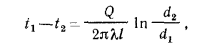
откуда

Полученное уравнение является расчетной формулой теплопроводности цилиндрической стенки. Оно будет справедливо и при 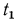
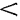
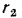 , т. е, когда тепловой поток направлен от наружной поверхности к внутренней.
, т. е, когда тепловой поток направлен от наружной поверхности к внутренней.
Для определения закона изменения температуры по толщине цилиндрической стенки подставим в равенство 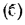 значения С из равенства (в) и Q из уравнения (13.7):
значения С из равенства (в) и Q из уравнения (13.7):
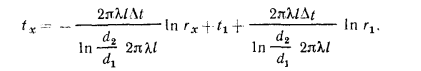
или
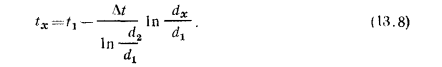
Равенство (13.8) представляет собой уравнение логарифмической кривой. При 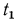
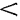 <
< 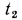 эта кривая будет направлена выпуклостью вверх (на рис. 13.4 она показана пунктиром)
эта кривая будет направлена выпуклостью вверх (на рис. 13.4 она показана пунктиром)
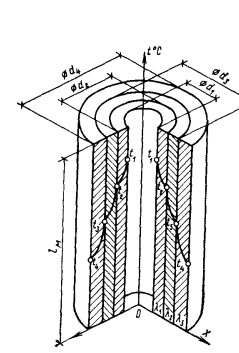
Плотность теплового потока для цилиндрической стенки может быть отнесена к единице внутренней поверхности 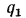 или к единице наружной поверхности
или к единице наружной поверхности 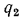 либо чаще всего к 1 пог. м длины трубы
либо чаще всего к 1 пог. м длины трубы 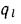 . В последнем случае
. В последнем случае
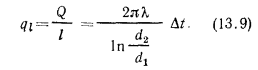
Соотношения между 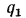
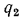 и
и 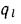 получают из равенства
получают из равенства
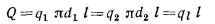
или
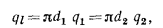
откуда
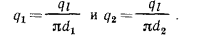
Величину 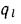 , Вт/м, называют линейной плотностью теплового потока.
, Вт/м, называют линейной плотностью теплового потока.
Факторы, влияющие на процесс теплоотдачи
Процесс теплообмена между жидкостью и стенкой, которую эта жидкость омывает, называется конвективным теплообменом, или процессом теплоотдачи. В этом процессе теплота передается одновременно путем теплопроводности и конвекции, и поэтому такой вид теплообмена представляет собой сложный процесс, зависящий от большего числа факторов по сравнению с процессом чистой теплопроводности.
- Конвективный теплообмен характерен для большинства процессов тепловой обработки строительных материалов и изделий, связанных с прохождением газов через слой материала, через садку изделий, над уровнями жидкостей при сушке и т. д.
Факторы, влияющие на процесс теплоотдачи, условно можно разделить на следующие группы.
I. Природа возникновения движения жидкости вдоль стенки.В зависимости от причины, вызывающей движение жидкости, различают два вида движения — свободное и вынужденное. Свободное движение, называемое иначе естественной конвекцией, вызывается подъемной силой, обусловленной разностью плотностей холодных и нагретых частиц жидкости. Интенсивность свободного движения зависит от вида жидкости, разности температур между отдельными ее частицами и объема пространства, в котором протекает процесс.
Вынужденное движение жидкости, или вынужденная конвекция, обусловлено работой внешних агрегатов (насоса, вентилятора и т. п.). Движущая сила при этом виде движения возникает вследствие разности давлений, устанавливающихся на входе и выходе из канала, по которому перемещается жидкость. Если скорость вынужденного движения небольшая и есть разница температур между отдельными частицами жидкости, то наряду с вынужденным движением может наблюдаться и свободное движение.
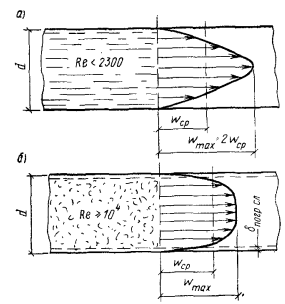
II. Режим движения жидкости. Движение жидкости может иметь ламинарный или турбулентный характер. В первом случае частицы жидкости в форме отдельных несмешивающихся струй следуют очертаниям канала или стенки и профиль скоростей на достаточном удалении от начала трубы имеет вид правильной параболы. Подобное распределение установившихся скоростей обусловливается наличием сил внутреннего трения (вязкости) между частицами жидкости. При этом максимальная скорость движения частиц жидкости, перемещающейся по оси трубы, в 2 раза больше средней скорости их движения, получаемой в результате деления секундного объема жидкости на площадь поперечного сечения трубы (рис. 14.1, а).
Турбулентный режим движения характеризуется непостоянством скорости движения частиц жидкости в рассматриваемой точке пространства. Из-за непрерывного перемешивания жидкости в ней нельзя выделить отдельные струи, и такое движение лишь условно можно назвать стационарным, считая для каждой частицы жидкости характерными не мгновенные, а усредненные за некоторый промежуток времени значения скорости. В этом случае профиль скоростей по сечению трубы будет иметь вид усеченной параболы и максимальная скорость, наблюдаемая у частиц жидкости, движущихся по оси трубы, будет всего в 1,2— 1,3 раза больше средней скорости. Характерно, что не все частицы жидкости при турбулентном режиме имеют неупорядоченное движение. Вблизи стенок, ограничивающих потоки, вследствие вязкости жидкости пульсации скорости уменьшаются, и около самой стенки сохраняется тонкий пограничный слой, движущийся ламинарно. В пределах этого слоя, который имеет толщину не более нескольких тысячных долей диаметра трубы, скорость движения частиц жидкости резко меняется от нуля на самой стенке до 0,4—0,7 средней скорости на условной границе с турбулентным ядром потока (рис. 14.1, б).
Строго говоря, турбулентные пульсации проникают и в ламинарный подслой и затухают в нем вследствие действия сил вязкости. Поэтому термин «ламинарный подслой» правильнее заменять термином «вязкий подслой».
Английский физик Рейнольдс установил, что при движении жидкости в трубах переход из ламинарного режима в турбулентный определяется значением безразмерного комплекса 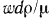 , в который входят средняя скорость w, диаметр трубы d*, плотность
, в который входят средняя скорость w, диаметр трубы d*, плотность 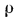 и динамическая вязкость жидкости
и динамическая вязкость жидкости 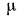 . Этот комплекс называют числом Рейнольдса и обозначают символом Re. При
. Этот комплекс называют числом Рейнольдса и обозначают символом Re. При 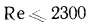 движение жидкости в трубах имеет ламинарный характер, а при
движение жидкости в трубах имеет ламинарный характер, а при 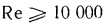 — турбулентный, т е. критическая скорость, позволяющая определить переход любой жидкости из ламинарного режима в турбулентный для трубы любого диаметра, может быть найдена из соотношения
— турбулентный, т е. критическая скорость, позволяющая определить переход любой жидкости из ламинарного режима в турбулентный для трубы любого диаметра, может быть найдена из соотношения 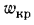
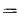
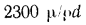 .
.
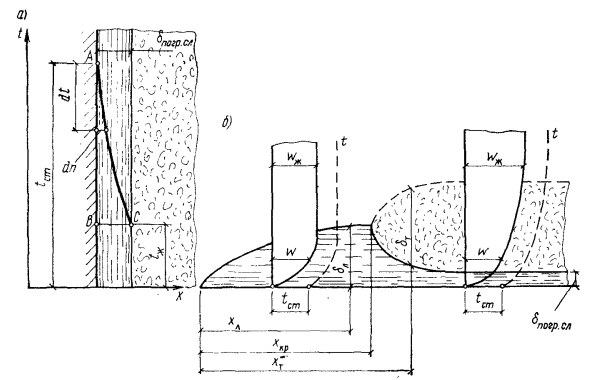
Следует также отметить, что наряду с описанным процессом формирования гидродинамического пограничного слоя происходит аналогичный процесс формирования и теплового пограничного слоя, в пределах
которого температура меняется от 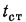 до
до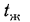 . Характер распределения температуры в тепловом пограничном слое зависит от режима течения жидкости в динамическом пограничном слое.
. Характер распределения температуры в тепловом пограничном слое зависит от режима течения жидкости в динамическом пограничном слое.
При ламинарном течении перенос теплоты между слоями жидкости осуществляется путем теплопроводности. В турбулентном пограничном слое основное изменение температуры происходит в пределах тонкого вязкого подслоя около стенки, через который теплота также передается путем теплопроводности.
по сечению трубы при ламинарном -(а) и турбулентном (б) режимах
В турбулентном ядре пограничного слоя вследствие интенсивного перемешивания жидкости температура изменяется незначительно (см. рис. 14.2, б) и поле температур имеет ровный пологий характер, т. е. отмечается качественное сходство в пограничном слое между распределением температур и скоростей.
III. Физические свойства жидкостей. На процесс теплоотдачи непосредственно влияют следующие физические параметры жидкостей: теплопроводность 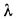 , удельная теплоемкость с,
, удельная теплоемкость с,
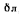 ,
,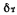 — толщина пограничного слоя соответственно ламинарного и турбулентного
— толщина пограничного слоя соответственно ламинарного и турбулентного
плотность р, а также вязкость и температуропроводность. Известно, что все жидкости обладают вязкостью, т. е. между отдельными частицами или слоями, перемещающимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. По закону Ньютона, эта сила F, отнесенная к единице поверхности, пропорциональна градиенту скорости 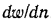 , т. е. F =
, т. е. F = 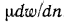 .
.
Коэффициент пропорциональности jx в этом уравнении называется коэффициентом . внутреннего трения или динамической вязкостью. При 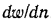 =1.
=1.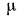 = F, т. е. динамическая вязкость численно равна силе трения, приходящейся на единицу поверхности соприкосновения двух слоев жидкости, скользящих один по другому, при условии, что на единицу длины нормали к поверхности скольжения скорость движения изменяется на единицу .Отношение
= F, т. е. динамическая вязкость численно равна силе трения, приходящейся на единицу поверхности соприкосновения двух слоев жидкости, скользящих один по другому, при условии, что на единицу длины нормали к поверхности скольжения скорость движения изменяется на единицу .Отношение 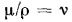 называется кинематической вязкостью. Если в комплексе
называется кинематической вязкостью. Если в комплексе 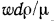 заменить отношение
заменить отношение 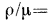
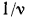 то число Рейнольдса принимает вид
то число Рейнольдса принимает вид 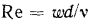 .
.
- Понятие температуропроводности тел связано с протеканием в них нестационарных тепловых процессов, наблюдаемых обычно при нагревании или охлаждении.
Скорость теплового процесса при нестационарном режиме определяется отношением 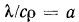 , которое называется температуропроводностью. Температуропроводность характеризует скорость выравнивания температуры в различных точках тела. Чем больше величина а, тем быстрее все точки какого-либо тела при его остывании или нагревании достигнут одинаковой температуры.
, которое называется температуропроводностью. Температуропроводность характеризует скорость выравнивания температуры в различных точках тела. Чем больше величина а, тем быстрее все точки какого-либо тела при его остывании или нагревании достигнут одинаковой температуры.
Единицей измерения динамической (абсолютной) вязкости 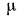 . служит
. служит 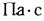 , а единицей измерения v и а —
, а единицей измерения v и а — 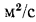 .
.
В настоящее время опытное определение коэффициента теплоотдачи производится, как правило, не на самих образцах тепловых устройств, а на их упрощенных моделях, более удобных для экспериментирования.
Результаты опытов, проведенных на моделях, обобщают, используя тепловую теорию подобия. Основной вывод, который делают на основе этой теории, заключается в том, что нет необходимости искать зависимость коэффициента теплоотдачи от каждого из тех факторов, которые на него влияют, а достаточно найти зависимость между определенными безразмерными комплексами величин, характерных для рассматриваемых условий процесса теплоотдачи.
Эти безразмерные комплексы величин называют критериями подобия. Составленные из размерных величин критерии подобия отражают физическую сущность, или, как говорят, модель процесса. Следовательно, задача заключается в том, чтобы найти вид зависимостей между критериями подобия, называемых критериальными уравнениями.
Теория из учебников тут.
Составляют критерии подобия с помощью дифференциальных уравнений конвективного теплообмена, т. е. уравнений, которые дают аналитическую зависимость между параметрами, характеризующими процесс теплоотдачи в дифференциальной форме.

