Оглавление:


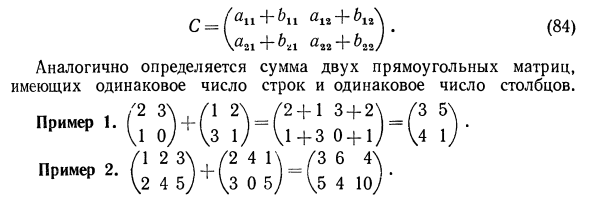







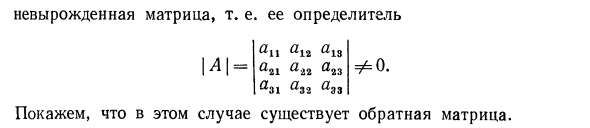



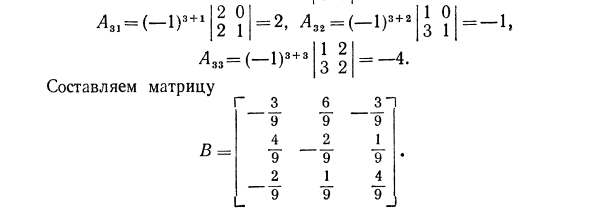





Матрицы и действия над ними
- МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ /. При изучении определений и систем уравнений (см. § 1) мы рассматриваем таблицу, составленую из (83) Эти таблицы мы назвали матричными, аП9 а12, … -элементами матрицы. Если в матрице число строк равно числу столбцов, то такую матрицу называют квадратной, причем число ее строк или столбцов называется порядком матрицы.
Так, например, в (83) первая матрица будет второго порядка, а последняя матрица-третьего порядка. (средняя матрица в (83). Матрица (ди а12 а13) наяро м атр и це й -стол бцом. Определитель, составленный из элементов квадратной матрицы, Мы будем обозначать одну букву, например: Это определенно будет матрицей.
Матрица, количество столбцов, которое называется прямоугольной Людмила Фирмаль
Так, например, если Л = ^ | и £ = _j)> то !) ■ (-! -IMS?) ‘• 3. Обратная матрица Матрица должна быть квадратной. Матрица называется Матрица, обозначенная как я. A-A ~ l = Е. (90) Вы можете выполнить равенство (90). А ~ 1-А = Е. (91) Приведем теперь следующую основную теорему. Теорема. Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. Е.
Чтобы ее определитель был отличен от нуля. … Доказательство Необходимость Предположим, что для матрицы А существует обратная матрица Л-1 Покажем, что в этом случае матрица А должна быть невырожденной, т е ее определитель | .. Л |. = £ 0 Действительно, если бы | Л | = 0, то определитель произведения \ A-A ~ 11 = | А |. | Л «11 = 0. Но это невозможно в силу равенства (91), из которого следует, что Л.Л-Ч = | £ | = 1- Достаточность. Пусть / ‘«11« 1з \ л = Я21 а% г а23 \ «3.« 32 «S3 /невырожденная матрица, т. е. ее определитель
ФО. все остальные«21« 22 «23« 31 «32« 33
| Элементы теории определителей | Линейные отображения |
| Системы уравнений первой степени | Плоскость |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Покажем, что в этом случае существует обратная матрица.В действительности, пусть Aik-алгебраическое дополнение элемента aik. 1) Составляем матрицу В, заменяем в матрице. Ли 12 Ау. В = Мл Мл Мл А 21 Л 22 ^ 23 Мл Мл Мл А 31 ^ 32 Л 33 А \ Ml | А 2) Составим новую матрицу В *} поменяв местами в матрице В ее строки и столбцы. (Матрица В * называется транспонированной матрицей по отношению к матрице В.) А ц А 21 Ля я 21 В * = Ml M 1 Ml А 12 Л 22 А 32 Мл Мл Мл л 13 ^ 23 л 33 А | | Л | | А Покажем, что матрица ~ Аи «И« 12 «13 Л- £ * = [« 21 «22« 23 А 21 31 а31 а32 азь / Мл Мл Мл А 12 Л 22 А 32 Мл Мл Мл Л есть Л 23 ^ 33 А ^ 11 ^ 11 + ^ 12 ^ 124-013 ^ 13 ОчА21 + а12А22 + а1яА23 аиАя1 + а12Л32 + О13Л33 «\ А \ \ А \ \ А \ ! a21 ^ 1I + Qr22 ^ 12 + Q23 ^ 13 q21 А 21 + ^ 22 ^ 22 + <* 23 А 23 021 ^ 31 + 022 ^ 32 + 023 ^ 33 \ А \ \ А \ \ А \ O.Tl ^ ll + 032 ^ 12 + 033 ^ 13 0,31 ^ 21 + Оз2 ^ 22 + fl33 ^ 23 О31 ^ 31 32 + 033 ^ 33 Мл Мл Мл
На основании формул (15) и (17) следует, что матрица, стоящая в правой части равенства (92), является н А-В * = Е, откуда следует, что В * = А ~ 1. Итак, 1и А ~ 1 = (93) ’21 ’31 Мл Мл Мл А12 А 22 ^ 32 Мл Мл Мл ^ 13 ^ 23 ^ 33 Ml Ml Ml и, следовательно, обратная матрица существует.Составим матрицу, матрикс второго порядка 12 21 «22 Здесь Axl-муравей Л12 = —аг1, Л21 = ~ а12, А = ап. = (аи аг \ a9t а. • ^ 11 ^ -12 21 ’22 мл А 22 -Ml Mfj В = дурак ’12 ’11 А \ J и «12 а 22 A ~ l = Мл «21 (93 ‘) II A I J Пример. / 1 2 О ‘А- = 3 2 1 V0 12 Решение. 1 2 О Л | = ‘ = —9. 3 2 1 О 1 2 Матрица А-невырожденная, и, следовательно, существует обратная ей матрица. Вычисляем алгебраические дополнения: 2 1 1 2 3 1 О 2 = 3, А12 — (- 1) 1+: = -6, = 3, = -4, Ли «(-1)» + » 3 2 О 1 Лз = (-1), + 3 2 О 1 О О 2 = 2, 1 2 1 2 О 1 2 + 3 = -1,
2 О 2 1 ’31 ^ 33 = ( Составляем матрицу В =2, Л32 = (-1) 3 + 2 1 2 _ 32 » 1 О 3 1 1) 3 + 3 В этой матрице, получим матрицу 1 9 9 А я 9 9 ‘ 1 1 9 9_ Обратная связь по величине: M ~ 4eyjp (94) Действительно, из формулы (90) А-А ~ 1 = Е. Применяя формулы (88) и (89), получим: откуда 4.
Предоставляем читателю проверить, что действительно А-А-1 — Е. Людмила Фирмаль
Матричная запись и матричное решение системы уравнений первой степени Применим рассмотренное в п. 2 этого параграфа правило умножения матриц к так называемому матричному способу записи уравнений. Пусть дана система уравнений «11 * 1 4 ~« 12- ^ 2 ~ Ь «13 * 3- ^ 1» a2lxt + a% fK + а23х3 = с2, ф. (95) «31 * 1 Н ~« 32 * 2 «33 * 3 = С3 ‘ Рассмотрим матрицу системы / «11« 12 «13 Л =« 21 «22« 23 \ «31« 32 «33, и матрицы-столбцы неизвестных и свободных членов с, Х = .С = 1 с2 с3
«31« 32 «33 / \ * 3 / \« 81 * 1 + «32 * 2 +« 33 * 3у Данную систему (95) можно записать, используя определенное равенство матриц (стр. 2), следующим обра «11 * 1 +« 12 * 2 + «13 * 3 211» I «22Л2 23 3,« 31 * 1 + «32 * 2 +« 33 * 3 » или, короче, Л-Х = С. (96) Равенство (96) называется матричным уравнением. Если система (95) записана в форме матричного уравнения (96) и матрица Л системы невырожденная, то решается это уравнение следующим образом. Умножим обе части уравнения (96) на матрицу Л «1, обратную матрице Л : А’1- (Л.Х) = Л-1-С. Используя сочетательный закон умножения матриц, можно написать (Л-1-Л) .Х = Л-1.Х. И так, как Л-1-Л = Е и Е-Х = Х Х = А ~ 1-С. (97) Пример. х1 + 2хг = 10, 3xt + 2хг + х3 = 23, хг + 2х3 = 13. «11« 12 «1з \ / * Д /« Ц * 1 + «1Л +« 13 * з ‘ «21« 22 «23 • * 2 =« 41 * 1 + «22 * 2 +« 23 * 3
В этой системе запишется система видеонаблюдения. 1 <Г / 1 2 0 \ / * Л А = [3 2 1, Х =, \ 0 1 2 / \ лг3 / была найдена в п. 3 3 9 9 1 J_ 3 9 9 9 Матрица А -1 А-1 =определитель матрицы В аи a2 a13 аг1 агг а23 В 1 = аз \ а32 азз Если определитель квадратной матрицы отличен от нуля, то матрица называется невырожденной. Если же определитель матрицы равен нулю, то матрица называется вырожденной. Например, матрица 2 3 \ А = 4 6 будет вырожденной, так как 2 3 = 26-3-4 = 0, И1- 4 6 а матрица ‘2 3N 4 5 В = невырожденной, так как 2 3 = 2-5-3-4 = -2 ^ = 0. В 1 = 4 5 2.
Равенство матрац. Равенство матриц. Две матрицы А и В называются равными (Л = Б), если они имеют одинаковое число строк и одинаковое число столбцов и их соответствующие элементы равны. Так, если А ^ (ап аА и Б = (бу М, то А «В, еслиаи = bllt \ а.п atJ \ bAl b2J Например, Яи аи / Ьи б ) 12 заполнить Ь22 А = («11 ~ 1г) и В = то их суммой называется матрица Решение системы записываем в виде (97): Х = Л ~ 1-С, или 4 2 3 9 9 _ Отсюда, на основании определения равенства матриц, следует: —4, * 2 = 3, х3 = 5. Непосредственной проверкой убеждаемся, что эти значения вестных удовлетворяют данной системе.
Се (* u + * 1I + (84) Равное количество двух прямоугольных матриц; ‘2 + 1 3-4-2’ Пример 1 .1 + 3 0 + 1. Пример 2.Легко проверить, что сложность матриц подчиняется перемести-тельному и сочетательному законам: Л + тф + (Л + Я) + С = Л + (В + С). Матрица, все элементы, которые равны нулю, называется нуль-матрицей и обозначается (0), или просто Нул-матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: Л + 0 = Л.
Например: / ви а19 W «22 Умножение матрицы на число. А = на число ц называется матрица \ ^ «2l \ xa2J Мы рассмотрели правило умножения матрицы на число для случая квадратной матрицы второго порядка. Совершенно так же умножается на число квадратных матриц третьего порядка и прямоугольные матрицы. Получается, что нуль-матрица: «И« и с, «21« 22у («И <* lt \ — (ъ 0 \ • 0 = , «21« 22 / \ 0 0, Умножение матриц.РРссмотрим правило перемножения двух квадратных матриц второго и третьего п. Л- (а »М и Б = фб» Ь ■ 4 ■ 14, 12 ч «21« 22 / V> 21 Ь,
Матрица С = А-В, элементы ксторой со «Л • В = (ailbil + ахгЬ * 1 аххЬх% + а12 ^ 2Л, (85) \ a2lbn — \ — arib.n aubl2 + arib 22 / Если даны матрицы третьего порядка л «1.« 12 «, з \ 6,2 ^ 13 «21« 22 «23) И В = 1 ^ 22 ^ 23 «3,« 32 «зз / * ^ 31 33. ^ 33 то матрица С — А-В составляется следующим образом: А-В = 21 «4» «13 ^ 31« 1А2 Н »« 12 ^ 22 »Ь« 13 ^ 32 «1Аз +« гАз 4 ~ «13 ^ 33 \ Н эт« Al «22 21» Г «23 ^ 31« 21 ^ 12 + «-« А »+« 23 ^ 2 «2 Аз +« 22 ^ 28 ~ T «23« J3 (• «« 3А1 Н ~ «32 ^ * 1 Н« 33 ^ 3 »« 31 ^ 12 «32 ^ 22 ~ Ь «33 ^ 32« зАз «Ь« 32 ^ 23 4 «« 33 ^ 33 / (86)
Как мы видим, элемент матрицы-произведения, находящийся на пересечении I-й строки и к-го столбца, представляет собой сумму парных произведений элементов I-й строки первой матрицы на элементы к-го столбца второй матрицы. Например, элемент, стоящий во второй строке и первом столбце матрицы произведения Л-Б, равен сумме произведений элементов второй строки матрицы Л на элементы первого столбца матрицы в.
Матрица прямоугольника. Пример 1 / 2 1 0 \ (Х2 / 2-1 + Ь2 + 0-2 2-2 + 1,1 + 0,2 \ / 4 5 \ \ 3 1 1/1 2 2 / \ 3-1 + 1-2 + 1-2 3,2 + Ы + Ь2 J = \ 7 9 / Пример 2. / ап аи \ / * Л / 4i * i + «12 * 2 \ # \« 2, «22 / Ш \ 0, Л + в« Л / В результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое, и столько столбцов, сколько их имеет матрица-множитель. Рассмотрим еще примеры умножения матриц. Пример 3. \ —1 2 / 1,3 1 / \ —Ь1 + 2-3 -1,1 + 2-1 У I / 1 1 \ / 3- / Ü3 + Ь (—1) 1 • (-1) 4- 1 -2 ‘ 3 1) \ — \ 2) —1) 3- (—1) 4-1-2. -GJ) — Не говоря уже о том, что А-В-А. Пример 4. В-А =
Можно проверить, что умножение матриц подчиняется сочетательному закону А- (ВС) = (А-В) ‘С и распределительному закону (А + В) С = А-С + В.С. Матрица второго порядка имеет особое значение Легко проверить, что при умножении на квадратную матрицу А-Е = Е-А = А. (87) Матрица Е называется единичной матрицей. Единичная матрица третьего порядка имеет вид Очевидно, что определитель единичной матрицы | £ | = 1. (88)
Можно показать, что если А и В-две квадратные матрицы одного порядка с определителями \ А \ и \ В \, то определитель матрицы С -А-В будет равен произведению определителей перемножаемых матриц, т. Е. | С | = | Л |. | Я |. (89) Пример 5. Пусть Л = «» «2) ‘!)’ Мы видели в пример 3, Определители этих матриц таковы:3 —1-1 2 1 1 3 1 О 2 5 -1 Л | = = 5, | Б | = = -2, | С | = = —10. Итак, действительно, М |. | В | = | С Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т. Е. Произведение двух ненулевых матриц может оказаться равным нуль-матрице.

