Оглавление:





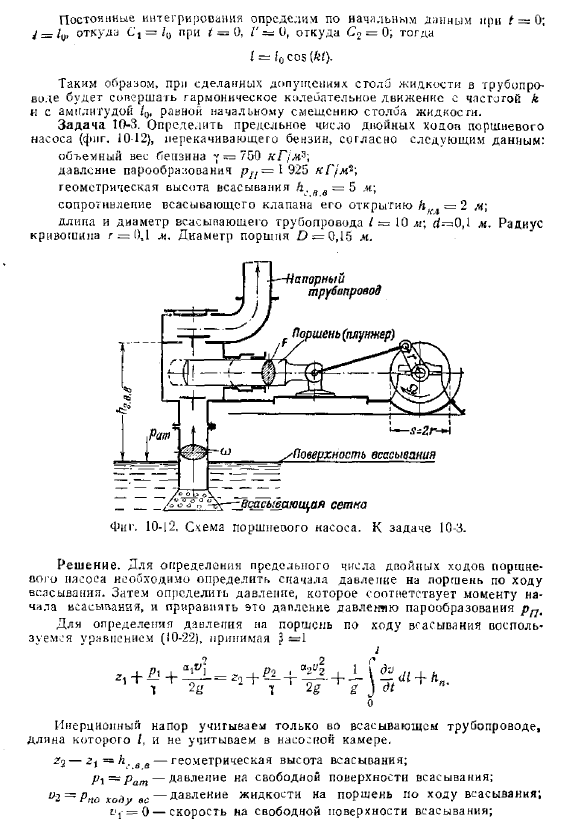


Примеры гидравлических расчетов установившихся и неусгановившихся потоков без учета гидравлических сопротивлений
Примеры гидравлических расчетов установившихся и неусгановившихся потоков без учета гидравлических сопротивлений. Я собираюсь отложить в сторону пот При определенной энергии за счет возникающего сопротивления Проанализируйте некоторые примеры жидкостей, не принимая во внимание при перемещении Эти losses.
Смотрите также:
В таких случаях основным уравнением является Уравнение Бернулли для потока, но без учета потерь энергии Непрерывное уравнение. При применении уравнения Бернулли в следующем виде (10-22) и (10-23) поток в общем случае имеет длину Однако сложная конфигурация в ограниченном разделе Рассчитанная длина проточного сечения, давление составляет Оно распределен согласно гидростатическому method. It также необходимо Так что значения r и p в каждом разделе соответствуют 1.
Смотрите также:
Наиболее подходящими для решения прикладных задач неустановившегося течения слабосжимаемой жидкости по трубам являются одномерные уравнения И.А.Чарного для средних по сечению трубопровода величин скорости и давления в функции от времени и продольной координаты. Людмила Фирмаль
В то же время. Задача 10-1. Создайте диаграмму Бернулли игнорируя сопротивление Для водопроводной трубы при следующих условиях. Эта система состоит из бака и пробки переменного поперечного сечения и концов Короткие трубки (рис. 10-10), что сходится в конусообразную форму. 1. Высота уровня воды на выходе из водохранилища n = 25 м На свободной поверхности давление Атмосферное. 2.
Смотрите также:
Для закрытых труб, то есть для стационарных жидкостей Энергия жидкости равна сумме потенциальной энергии конкретного места И давление. Потому что все точки неподвижной жидкости имеют одинаковую энергию ГИА, проще всего определить по очкам, которые находятся в свободном Приводная поверхность в баке. Сравнение плоскости для выбора прохода Из центра розетки.
Очевидно, что эта энергия равна. И тогда = g + p = 35 м Где r = a = 25 и*; —10 м (равное атмосферное давление 10000 кгг1м-4, и / = 1 ООО кгг / Л3). Энергетическая линия неподвижной жидкости будет представлять собой горизонтальную линию Он расположен на высоте 35 м (обозначен пунктирной линией). § 10-8] примеры расчета расхода кроме гидроэлектростанций.
Любой участок трубы Определяется по ряду жидкости yotosyv З-П, которая Я. .На рисунке показан разрез com заключенный между пунктами Энергия и пунктирная линия оси Согласно трубопроводу Участок трубы .В случае с поло Пьезоэлектрические проволоки Вы можете изменить его .как построить Диа Вам нужно определиться с программой Поток жидкости б Разные части акведука .
Сначала определите скорость В разделе выход .Для этого, во-первых Бернулли пишет уравнение 2 раздела: первый Значение{0-0) выбирается независимо Повторно водной поверхности Водохранилище; 2-й{4-4) и Плоскость выходного отверстия Стиль .В разделе 0-0 рассматриваемого случая, давление Гидростатический метод, и в разделе 4-4 давление составляет P .•= 1 <1ет .Итак, уравнение Бернулли выражается как: Л о РС И фигура тоже .10-10 .
Имеющиеся экспериментальные данные дают лишь качественную картину неустановившегося турбулентного течения. Людмила Фирмаль
- Иллюстрация уравнения Бернулли .К выпуску 10-1 .Определите значения для каждого члена уравнения Бернулли .В рассматриваемом случае он может быть равен коэффициенту Единицы $ 4= 1; * Получите плоскость сравнения, как показано на рисунке Давление ha на выходе из трубы в атмосферу принимается равным атмосферному Номинальный.) Подставьте значения, найденные в уравнении Бернулли, чтобы получить следующее.
Поток постоянный, то есть гидродинамическая линия Ролик выравнивается. Если известна гидродинамика, то определяется положение этой линии Точечное давление, например, точка, которая находится на Уровень жидкости и резервуар; В. Таким образом, линия полной удельной энергии (гидродинамики Давление) размещается на горизонтальной плоскости с высотой i ^ d = 35М Над сравнением plane.

