Элементы теории определителей

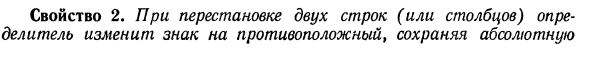
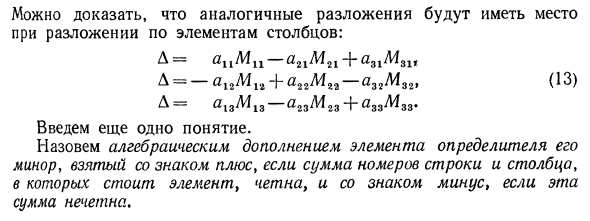
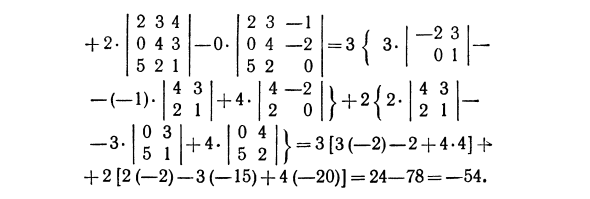
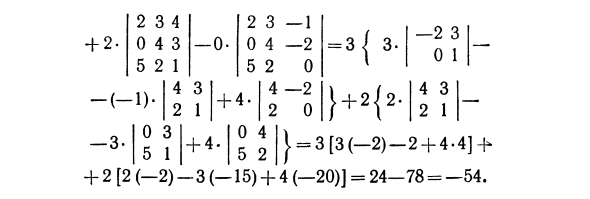
• <nav class=»toc»> 
  <h2>Содержание:</h2> 
  <ul> 
  <li><a href=»#1″>Элементы теории определителей</a></li> 
  <li><a href=»#2″>Примеры решения и задачи c методическими указаниями </a></li> 
  </ul> 
  </nav> 

• <h2 id=»1″>      Элементы теории определителей       </h2>

• Элементы теории определителя. Квадратичные детерминанты и их свойства Таблица, состоящая из четырех чисел (называемая матрицей) дается: 「11」 12 「21」 22 Матрица имеет две строки, apa12 и a21a22, и 11 и два столбца. «21» 22 Числа, составляющие эту матрицу, обозначены буквами с двумя индексами. Первый индекс показывает номер строки, а второй индекс показывает номер столбца, в котором находится этот номер.

. Номер А12, А2ЛТ 22 Это называется матричным элементом. Квадратичный определитель (или определитель), соответствующий данной матрице, представляет собой число, полученное как apa2r — a21a12. Идентификатор обозначается символом «А» 12 «21» 22 Вот так (1) но 12 — 」11」 22 「12」 21 * 「II」 12 「21」 22 (2) Числа an, a12, a21 и a22 называются определяющими элементами. -2 — (- 4) -5-3 = -23. 2 5 3-4 Пример. Дает характер квадратичного детерминанта. Свойство 1. Если строка заменяется соответствующим столбцом, то есть определитель не изменяется. «H« 12 «11« 21 「21」 22 「12」 22

Например, a12 означает номер первой строки и второго столбца. A21 — числовое значение 2 на 1 Людмила Фирмаль

«CL» + a1gA22 + al3Ai3 = ai (-M21) + aX2Mg + a19 (-Mn) = i 「11」 13 「31」 33 — «11 (» 12 «33-» 13 «32) 4-» 12 («11» 33- «13» 3л) — «13 (» 11 «32—» 12 «3л) = ~ «11« 12 «33 +« 11 «13« 32 + «12« 11 «33« 12 «13« 31- «13« 11 «32 +« 13 «12« 31 = Оставшееся равенство проверяется таким же образом. 11 11 12 31 32 • 12 «13 + » -А 11 12 13 「32」 33

Понятие детерминантов высшего порядка Для многих задач вы можете найти определители высшего порядка в дополнение к определителям второго и третьего порядка. Например, определитель четвертого порядка ap avl a1I ai a21 agg a23 ai 31 '' 32 33 » 34 41 '' 42 40 » 44 «11» 11 «13 ••« .ft ‘• «1П «21» 22 «23 ‘•» 2 фута •• «2л «/ 1» / 2 «/ ч ••« / фут •• «/ л «« 1 «I * ap s ..» «ft ‘•« ll Определитель четвертого порядка вычисляется с использованием того же уравнения, что и уравнение (8). D = «21» 23 «24» 21 «22» 24 «21» 22 «23 12 '' 31 33 » 34 + 13 '' 31 32 » 31 14 '' 31 32 » 33 41 '' 4, 44 » 41 4 2 '' 44 41 » 42 43

• Решение задач по высшей математике

Уравнение линии	Системы уравнений первой степени
Преобразование координат	Матрицы и действия над ними

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Кубический определитель в правой части уравнения называется младшим из элементов aLl, d12, al3 и alv. Как и раньше, показывая алгебраическое дополнение элемента aik А.ik., определитель четвертого порядка Д может быть выражен как: D = И вообще, определитель n-го порядка A- 「11」 12 「13」 14 「21」 22 「23」 24 31 » 32 33 '' 34 41 » 42 « 43 » 44 「22」 23 а = «11» 32 «33 a 「42」 43 а

b = axxAxx + altAx% + aX9AX9 + aXAA Эта формула разбивает определитель четвертого порядка на элементы в первой строке. Определители высшего порядка вычисляются таким же образом. Все свойства определителей второго и третьего порядка действительны для любого определителя порядка. Пример. Вычисляет определитель четвертого порядка 2-14 0. 0-2 3 | 5 0 1 D = 2 3 4 + 2- 0 4 3 -O- 5 2 1 4 2 Около 3 5 1 2 3—1 0 4—2 5 2 0 I 4 —2 ‘I 2 0 —2 3 0 1 4 3 2 1 3 1 + 4 } +2 { — (- 1) + 4 0 4 5 2 = 3 [3 (-2) -2 + 4-4] -j * -3. + 2 [2 (-2) -3 (-15) +4 (–20)] = 24-78 = -54.

Свойство 2. 3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю. Свойство 4. Общие факторы для всех элементов в строке (или столбце) могут быть получены по признаку определителя. (5) Свойство 5. Если все элементы в строке (или столбце) равны нулю, определитель равен нулю.

При перестановке двух строк (или столбцов) определитель меняет знак на противоположный и сохраняет абсолютное значение «А» 12 «21» 22 «21» 22 «и» 12 Свойство Людмила Фирмаль

Свойство 6. Если соответствующий элемент другой строки (или столбца), умноженный на то же число, добавляется в строку (или столбец) определителя, определитель не меняет своего значения. Значение, т.е. «И » 12 = k «11» 12 «21 ка22» 21 «22 Любовь + привет apl + ha 「12」 11 「12 「22」 21 「22 И 21 год (6) Все свойства квадратичного определителя подтверждаются простой проверкой на основе правил для вычисления определителя (уравнение 2). Например, давайте докажем свойство (6). Для этого вычислите определитель в левой части уравнения (b). = +% Ai) a2- (a21 + xa22) a12 «11» 22 + ^ «12» 22- «21» 12- ^ «22» 12 = «11» 2 «-» 21 «12 = «11 + ^» 12 «12» 21 + ^ «22» 22 «11» 12 « 1″ 22 2. Третьи определяющие факторы Рассмотрим таблицу (матрицу), состоящую из девяти чисел. «А» 12 «13 \ «21» 22 «23 • (7) «31» 32 «ЗЗ /

«21» 22 -А 11 «31» 32 Кубический определитель «11» 12 «13» 21 «22» 23 «31» 32 «33 「22」 23 「32」 33 «21» 23 «31» 33 но 13 12 Кубический определитель (или определитель), соответствующий этой матрице, представляет собой число, полученное следующим образом:Числа dp, …, x83 называются их элементами. Кубический определитель имеет три строки и три столбца. Вот так 「11」 12 「13」 2 1 「22」 23 「31」 32 「33 「21」 22 「31」 32 「22」 23 「32」 33 «21» 23 «31» 33 (В) ~ B «1: -a -a что 12 Уравнение (8) разлагает кубический определитель по элементам в первой строке aa ^ a13 и сводит вычисление кубического определителя к вычислению квадратичного определителя.

Мы будем называть минор, соответствующий этому элементу кубического определителя, квадратичным определителем, полученным из этого кубического определителя путем удаления строк и столбцов, которые этот элемент пересекает. Несовершеннолетние обозначены заглавной буквой М с двумя индексами. Так, например, у каждого с минорным М12 Соответствующий элемент a12 является определителем Mn = «21» 23 «31» 33 он получить,. , Чтобы удалить первую строку и второй столбец из кубического определителя.

Уравнение (8) показывает, что кубический определитель равен алгебраической сумме попарного произведения элементов в первом ряду на соответствующий минор. В этом случае минор, соответствующий элементу a12, получается как знак минус. Перепишите соотношение (8) в следующей форме, используя правило вычисления квадратичного определителя: ~ «11» («22» 33 «32» 2e) «12 (» 21 «33 ~» 3 1 «2з) + + «13 (» 2 1 «32 ~~~~» 31 «2d) ==» 11 «22» 33 «11» 32 «23 *» 12 «21» 33 + «12» 31 «23 +» 13 » 21 «32» 13 «31» 22 * Пример. 「11」 12 「13 「21」 22 「23」 31 「32」 33 23 ~ 4 ФИ 71 5 6 7 = 2. ^ I —3 • 8 0 3 = 2-18-3 • (-41) -4 • (-48) = 351. 5 7 8 3 5 6 8 0 + (-4)

Все свойства квадратичных определителей (см. Раздел 1) действительны для кубических определителей. Доказательство этих свойств кубического определителя ничем не отличается от доказательства аналогичных свойств квадратичного определителя и основано на вычислении кубического определителя по уравнению (8). Мы рекомендуем вам доказать эти свойства самостоятельно. Детерминанты могут быть разложены на произвольные элементы строки или столбца, аналогично уравнению (8), которое разбивает кубический определитель на элементы в первой строке.

Например, разложение определителя на элементы во втором ряду можно получить следующим образом: Второе свойство (см. Раздел 1) 「11」 12 「13」 21 「22」 23 «21» 22 «23 = -» 11 «12» 13 • С) «31» 32 «33» 31 «32» 33 Разлагает определитель справа на первый ряд элементов. Согласно правилам расчета определителя, «21» 22 «23» 11 «12» 13 «31» 32 «33 」12」 13 「32」 33 」11」 13 「31」 33 «А» 12 «31» 32 + а = а -a 21 22 23 Учитывая равенство (*) 21 」12」 13 「32」 33 22 「11」 13 「31」 33 По модификатору 「12」 13 「11」 13 「И」 12 «32» 33 f «31» 33 «» 31 «32 Суть несовершеннолетних Это модификатор тов а21, а22, а23. Уравнение (10) разбивает определитель на элементы второго ряда. Докажите то же самое, заменив первый ряд на третий. какие 「11」 12 「13 (Р) 「21」 22 「23」 31 「32」 33

Уравнение (11) разбивает определитель на элементы в третьей строке. Когда этот кубический определитель представлен A, уравнения (8), (10) и (11) записываются в следующем формате. D = anMn — anMl2 + al3Ml8t D = -a21M21 + a22M22 — a23M23, (12) D = a31M31 — a32M32 + a3SM 33. 「11」 12 「13 「21」 22 「23」 31 「32」 33 「11」 12 「31」 J2 (U) —a -А 23 」12」 13 「22」 23 「11」 13 「2 1」 23 «11» 12 «21» 22 + » -a -А 31 33 32 Вы можете доказать, что аналогичная декомпозиция происходит при декомпозиции на элементы столбца. D = ACMC-a21M21 + a31M31, A = -al2M 12 + a2gM „-a32M32, (13) D = al3Ml3 — a23M23 H-a33M33. Вот еще одна концепция. Вызывает несовершеннолетний, который принимает алгебраическое дополнение детерминантного элемента со знаком плюс, если сумма номеров строк и столбцов, используемых в элементе, является четным числом и знаком минус, если сумма нечетная.

Алгебраическое дополнение a1k есть A {k. Где i — номер строки, k-номер столбца пересечения, в котором расположен этот элемент. Соотношение между алгебраическим дополнением элемента и его минором определяется следующим уравнением: LL “(-1) ‘+ * ML. (14) Пример: Au = <—1) 1 + 1M „= Af„, = (-1) 1 + 2M12 = -M12. ^ 13 = ^ 13 и т-д- Легко видеть, что уравнения (12) и (13) для вычисления определителя можно переписать следующим образом: A = apAn + a12 Ai + a13 A la, A = «21 21 22 23» (15) A = «31 ^ 31 +» 32 ^ 32 «b» 33 ^ 33 Разложить определитель на линейные элементы, А = аиАп + а.пАг1 + а31А31, А = я12Л12 + a22A 22 32 32 (16) A = yhzAuz + «23 ^ 28» 33 ^ 33 Разлагает определитель на элементы столбца. Результат можно сформулировать следующим образом: Кубический определитель равен сумме попарного произведения любого элемента строки (или столбца) и их алгебраического сложения. Показывает другую важную характеристику кубических определителей «11» 12 а «21» 22 а «31» 32 a Сумма произведений элементов в строке (или столбце) определителя алгебраическим дополнением соответствующего элемента в другой строке (или столбце) равна нулю. Например «IAi + altAi2 + alsAi8 = 0; (17) Для столбцов: u12A11 — \ — a22A2l-j-a32A3l ^ 0 (18)