Оглавление:




Дифференциальные уравнения движения реальной жидкости (уравнения Навъе-Стокса)
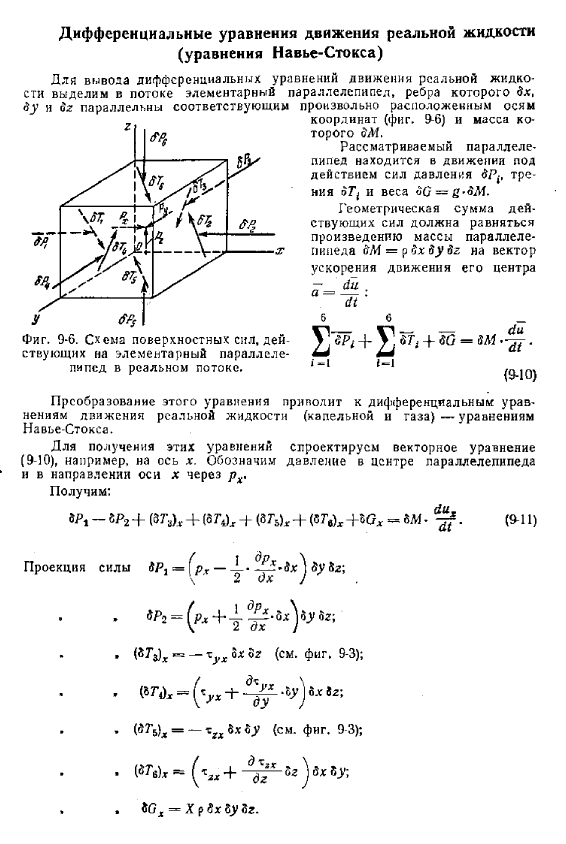
Дифференциальные уравнения движения реальной жидкости (уравнения Навъе-Стокса). Вывести дифференциальное уравнение для реального движения жидкости В flow выберите базовый параллелепипед ребра dx. Выполнить и параллельно оси соответствующего случайного интервала Координаты (рис. 9-6) и масса co Тпру. Рассматривать как параллельные Труба движется вниз. Действие давления d p tre Ния и веса ОО = Геометрическая сумма действий Силы должны быть равны Параллель массового производства pipeda&m =p bx dx dg на вектор Ускорьте движение своего центра тн1. И фигура тоже. 9-6.
Смотрите также:
Система уравнений Навье-Стокса дает очень точные решения, если рассматривается ламинарное течение жидкости, либо геометрия каналов несложная. Людмила Фирмаль
Схема поверхностных сил, сутки Основная параллель Он передается по трубопроводу к фактическому потоку. Да. Б 6. 1 = 1 Номер 10. Преобразование этого уравнения приводит к дифференциальному уравнению Уравнения движения жидкостей (капель и газов) Навье Стокс. Чтобы получить эти уравнения, разработайте векторное уравнение (9-10), например, по оси x. Указывает давление в центре параллелепипеда И направление оси x через px.
Смотрите также:
Гидродинамическое давление в данном направлении.
В последнем уравнении x-проекция ускорения на ось x Проекция на ось тяжести и вектор единственного ускорения И. .Да .Ксения .Это .. Потому что мощность преступника равна нулю в проекции остальной мощности на ось x Уникально для оси проекции. Подставляя значение силы, полученное по формуле (9-11) п bxbxr, уравнение движения + (9-12 Р ДХ » п в ды ^ ДГ) 6. 1 Можно получить аналогичное уравнение с проекцией на ось + ^ = (9-13 Р дю Р ДХ ^ ДГ) <11 ′* 2 _ 1 Почта+ 1 (^ + ^ m»^. (И4 Р ДГ Р ДХ делать} Далее мы делаем детальное преобразование только для уравнений (9-12), заменить в этой формуле по формуле (9-8)
Из уравнения неразрывности жидкости до капли А потом, конечно, Ди, Ди, Ди .* ___ 4 _ 4— !^ „<адрес>“ .ДХ ^ ду ^ ДХ С помощью этого уравнения дифференциальное уравнение движения Он принимает следующую форму: г д-р, Уравнения (9-15) (9-17) и (9-18) (9-20) называются уравнениями Навье * Стокса .если q = 0, то эти уравнения используются в сочетании с уравнениями Эйлера .Изучите уравнение (9-18) — (9-20) о возможности движения .День Если вы используете зависимости (7-17), это будет выглядеть так.
На практике система уравнений Навье-Стокса применяется для расчёта конвекции и термической диффузии в теплофизике и теплотехнике; для предсказания поведения смесей, состоящих из многих компонентов. Людмила Фирмаль
Аналогично, если подставить эти значения в Формулу (9-18), то она будет выглядеть так: ^-1 ^ + 1 1 4д^у4 -^) =аЛ. Но согласно уравнению неразрывности § 10 1] Прямая трансляция раздел 143 Итак, уравнения Навье-Стокса для потенциального движения Он имеет следующий вид: (0-21 т . к .Но по внешнему виду эти уравнения ничем не отличаются от уравнений Эйлера .Но В этих уравнениях, в отличие от уравнения Эйлер .ГХ + РУ + РГ П = 3 .№ .С . Жуковский указал на следующее: Вязкость не влияет на движение внутри жидкости .Это не влияет на распределение внутреннего давления .
Смотрите также:

