Оглавление:








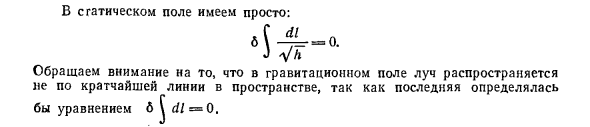

Постоянное гравитационное поле
- Постоянное гравитационное поле. Гравитационное поле называется постоянным Получите систему отсчета, которая содержит все метрические компоненты Тензор не зависит от временной координаты x0. отава Нагота называется мировым временем. Выбор мирового времени не совсем понятен.
Таким образом, добавить любую функцию пробела к x ° Все ординаты не включают w0. Это раньше Развитие отвечает на желание выбрать ориентир Время 1) в каждой точке пространства. Кроме того, Конечно, мировое время можно умножить произвольно. Произвольный выбор констант, то есть единиц изменения Рений. Строго говоря, только поля являются константами.
Национальная привлекательность ведет к движению В результате созданные ими поля не могут быть константами Людмила Фирмаль
Мое тело В некоторых объектных системах их взаимная гравитация Nim Если тело, которое создает поле, не перемещается (в пределах системы отсчета, Где g ^ не зависит от x0), оба направления времени Это эквивалентно.
Путем соответствующего выбора контрольного времени Все точки в пространстве, в этом случае расстояние ds Все компоненты Гоа, потому что х0 меняется при смене знака Метрический тензор также должен быть таким же Ли. Такое постоянное гравитационное поле называется Статическая. Однако физическая неподвижность не обязательна.
- Лови неизменность созданного им поля. Так что есть константы Кроме того, поле, которое вращается равномерно вокруг своей оси Осесимметричное тело. Но в этом случае оба направления Время никогда не бывает эквивалентным — когда знак меняется С течением времени знак угловой скорости вращения изменяется.
И поэтому Такое постоянное гравитационное поле Компонент метрического тензора Гора (называемый статическим) Вообще говоря, это ненулевое значение. Значение мирового времени в постоянном гравитационном поле В факте его разрыва между двумя событиями Совпадают с расстоянием в некоторой точке пространства Между двумя другими событиями в других точках Пространство, каждый одновременно (в § 84 смысла) Первая пара событий.
В слабом гравитационном поле вы можете использовать Приближенное выражение Людмила Фирмаль
Но та же свадьба Spooky World Time X ° реагирует по-разному Сделайте различные интервалы в подходящее время t. Соотношение (84.1) между ними можно описать в следующем формате: r = -cV м х °, (88,1) Применимо к концу разрыва. (87.12); (88.1) то же самое Точность: — = m (1 + 10- <88’2>
Поэтому мое время течет Меньше гравитационного потенциала в определенной точке пространства Состояние, то есть его абсолютное значение больше Это показывает, что потенциал IP отрицателен). 2 случая В то же время, некоторое время было гравитация Время, которое было в поле, а затем поле Sutoragura.
Как уже показано, в статическом гравитационном поле Гоа-компонента метрического тензора равна нулю. По словам В результате §84 это означает, что такая синхронизация поля возможна Часы идут вниз во всех местах. Об элементе пространственного расстояния Есть просто статические поля dl2 = —gapdxadxP. (88,3) В стационарном поле Гор не равен нулю и синхронизирован Несколько часов не возможно во всех местах.
Потому что г ^ не зависит Уравнение разницы в мировом значении как функция x0 (84.14) Время двух одновременных событий, которые происходят в разных Пространственные точки могут быть записаны как х ° = — [(88,4) J & OO Применимо к двум точкам на линии Синхронизация стека часов.
При синхронизации По замкнутому циклу разница в значениях мирового времени, Обнаружен при возврате в начальную точку. Постоянное поле тяжести337 Равно целому х ° = — (С (88,5) / Гу Взятые по этой замкнутой петле 1). Рассмотрим распространение лучей в постоянном гра Жизненное поле.
У нас есть частота света Эйконал f производная по времени (противоположный знак). чай Следовательно, заикание, измеренное в мировом времени x0 / s, равно ujq = = —Sdf / dx®. Уравнение Эйконала (87.9) является константой Если поле явно не содержит x0, частота luq равна Луч света Частота, измеренная Номинальное значение времени, равное w = —dp / dt \ Пространство.
Для отношений df _ df dx ° _ df s дт дх ° дт дх ° л / гу IMEVM w = ^ -. (88,6) год назад В слабом гравитационном поле: w = w0 (1-> y (88,7) Вы можете видеть, что частота света увеличивается с увеличением Величина потенциала гравитационного поля, т. Е. Подойдите ближе к телу, которое создает поле.
Наоборот при удалении Луч от этих объектов уменьшит частоту света. Для лучей Гравитационный потенциал испускается в точке, равной <пи, Имеет частоту si (на данный момент) и достиг потенциальной точки циалом (р2, есть частота (измеряется независимо Равен времени на данный момент) 1- (пи / с Линейный спектр испускается атомом выше Например, прогулка на солнце выглядит точно так же, Как спектр, испускаемый ими на Земле, выглядит на Земле Она с таким же атомом.
Если спектр наблюдается на земле, Излучается солнечными атомами следующим образом Из вышесказанного, линия Линии одинакового спектра излучаются на землю. То есть каждая строка с si-частотой сдвигается на inter. Вал определяется действием, формула Где (pi и (p2 — потенциалы гравитационного поля Точка излучения и точка наблюдения спектра.
В случае Земли Спектры, испускаемые солнцем или звездами, наблюдаются \ <Pi \> | ^ 21 и (88,8), Dei <0, т.е. происходит смещение Идите к более низким частотам. Описанное явление Redshift. Я понимаю происхождение этого явления Основано непосредственно на мировом времени выше Оба не имеют времени.
Постоянство поля, мировой интервал времени, Некоторые колебания в гонке световых волн в то же время Расширяться из одной точки в пространстве в другую Я не зависим от х0. Поэтому количество вибраций, которые происходят Каждая единица мирового времени одинакова Точка вдоль луча.
Но тот же разрыв является глобальным Время Время, мы далеки от создания Следовательно, лютеранская частота, то есть частота в единице Мое время падает, когда свет убирается Из этих масс. Когда частицы движутся в определенном поле, Энергия определяется как производная действия (–cdS / dx®) До мирового времени. Это, например, х ° Оно не включено явно в уравнение Гамильтона-Якоби.
конечно Таким образом, энергия является временным компонентом ковариации Четыре вектора импульса pj ~ = tsi & = mcgkiU1. статически Поле ds2 = goo (dx °) 2-dl2, а для энергии Вот §§: Эш =! ^1 ^! P1 и (88,8) s / goo (dx0) 2-dl2 дх ° Вот скорости частиц: Поле постоянной гравитации339 Измерено в соответствующее время, т.е. наблюдателем На этом месте.
Тогда получите энергию A _ mc2 ^ m (88 г / л-V2 / C2 Это значение, которое остается постоянным при движении НИИ частиц. Нетрудно показать, что выражение энергии (88,9) остается Если измеряется только скорость v, в силовом и стационарном поле Синхронизируется в подходящее время, определяемое часами Вдоль траектории частицы.
Когда частицы отделены ки и наступи бесконечно в момент всеобщего времени х0 Момент х ° + б? Закройте точку B на x °, затем определите скорость Вы должны взять -x ° = dx ° вместо временного интервала (x0 + dx °). И разница между x ° + dx ° и моментом x ° — dxa Goo Одновременно в точке B со временем x0 в точке A: (X ° + dx °) — (x ° — ^ dxa) = dx ° + ^ dxa. V Goo / Goo
Умножение на y’goo / c> дает соответствующий интервал Скорость, потому что это подходящее время И DXA г / ч (дх ° -гадха) ’ Где введена нотация (88.10) ga = -, h = goo (88.11) Goo Трехмерный вектор g (уже упомянутый в 84) и Трехмерная скалярная гуковариантная составляющая скорости v Соответствует как трехмерный вектор в пространстве с метрикой 7a / #
Следовательно, квадрат этого вектора равен 1) Va = 7a / 3 * 1 V2 = вава. (88.12) В этом определении интервал ds равен Скорость по той же формуле, что и обычная формула ds2 = goo (dx0) 2 + 2goadx ° dxa + gOL ^ dxadx ^ = = h (dx ° -gadxa) 2-dl2 = h (dx ° -gadxa) 2 ^ 1-. (88.13) 4 составляющих скорости u = dx1 / ds равны и, =, = ау 0 _ 1 | gocV ~ u = — + — (88.14) Su / 1-v 2 / c 2 y / h y / l-V2 / s 2 Сy / l-V2 / s 2 Энергия <R0 = mc2goiUl = mc2h (u ° -гауа) После замены (88.14) принимает вид (88.9).
Для слабых гравитационных полей и малых пределов Подставляя скорость, goo-1 + 2 ^ / s2 в (88,9), о Женат <R0 = mc2 + + pir, (88,15) Где ggcr — потенциальная энергия частицы в гравитации. Соответствует функциям Ле и Лагранжа (87.10). Задача 1. Определить силу, действующую на частицу с постоянной силой тяжести На поле.
Решения. Для необходимых компонентов вы найдете: Ярость: R0 o = \ h’a, r & = f a-g f) — \ g ^, h i (1) = а? h + -eft) + & M a ~ «W +» • В этих выражениях все тензорные действия (ковариантные Индексирование, повышение и понижение индекса) выполняется в трех измерениях Пространство с 3D вектором ga и 7 метрической метрикой на 3D Скалярный h (88.11); AJg7 — созданный трехмерный символ Кристоффеля.
Это то же самое, что компонент тензор jap состоит из компонентов Tg и gik. При расчете использовалась формула (84,9) — (84,12). Подставляя (1) в уравнение движения du «_ — ГоQ, о, (^ 0 \) 2 из» 01О и Р-пРи7 в качестве После простого, используйте уравнение (88.14) для 4-скоростной составляющей Конверсию получаем d V h {g «e-g ° y \% y v> d a / 1-v2 / c2 2h (l-v2 / c2) c (l-v2 / c2) c2 (l-v2 / c2) Поле постоянной гравитации341
Сила f, действующая на частицу, является производной ее импульса p К соответствующему времени (синхронизировано) Трехмерное ковариантное дифференцирование: „A _ L v2 Dpa _Гу2d mvaаmv ^ y1 y c2 ds y c2 ds y / l-y2 / s2 y / l-y2 / s2 Следовательно, из (2) (индекс a опущен для удобства) И = (_ _9_1 v / 1-v2 / c 2 I ftr’3 ‘s / Или нормальная трехмерная векторная нотация 1) f = m C v 2 / s 2 {˜grad b A + A r ° t g]}. (3) Если тело не движется, сила, действующая на тело ( Существует возможность в последнем члене (3).
Второй на низкой скорости Термин (3) имеет вид mcy / h [v rot g] и аналогичен силе Кориолиса. Происходит во вращающейся системе координат (если поля нет) 1) В координатах трехмерной кривой единица измерения асимметрична Тензор определяется как / -ive 7 1 пр 7 D) a1z7 = V 7 va / 37 »V = -e, «L Е = 32 i 6 ед. R12 Я-I = 1, и если перестановка двух индексов меняет знак (Ср. (83,13), (83,14)).
Таким образом, вектор с = [ab] определением В качестве дуального вектора асимметричных тензоров c / d7 = a / db7-a7 b / d Компонент 1 / -in’u / -in i 7 sc 1 хорошо 7 7 av’u t == V7 e <* / s7c = yn ^ osma b «, c = -en = -e / a / 3o7. 2 2 ^ / 7 \ / 7 Обратное: ca / s = yfieapyc1, ca? = ± ea / 9%. л / 7 В частности, rot a следует понимать в том же значении, что и вектор двойственного
Это верно Для тензора ar- / s = ————- s-, его контравариантная составляющая Dadar (R o tа) «= -еаМ (Щ_д? Ј \ ‘ 2 года / ^ лет Udh13 дх ~ <> В этом контексте трехмерная дивергенция вектора Дива = (Ср. (86,9)). Часто, чтобы избежать путаницы при сравнении с формулами
Может быть решена с помощью трехмерной векторной операции с ортогональной кривизной Линейные координаты (например, см. Электродинамика сплошных сред. Приложение), с этими формулами под векторной составляющей Означает количество x / giTA1 (= y / AiA1), ^ Jg ^ A2, ^ / g3 3 A3. Угловая скорость фут = -у / ч гниль 2 2. Вывод принципа Ферма для распространения постоянных лучей Гравитационное поле.
Решения. Состояние принципа Ферма (см. § 53): 8 J xx dxa = O, Интеграл берется вдоль луча, а подынтегральное выражение Выражается постоянной частотой ujq вдоль луча и производной Координаты. Обратите внимание, что k0 = —dp / dx ° = ujq / c, ^ = ko = goik * = gook0 + gOaka = h (k ° -гака).
и Подставляя это в отношение kikг = gikklkk = 0, оно будет записано в виде h (k ° -gaka) 2-Japkak ^ = O, Мы получаем l (~) «Va / 3 ^ k13 = 0. я буду Учитывая также, что вектор ka должен иметь направление вектора dxa, Найти здесь И _ UJO DXA ~ Cy / H дл Где dl (84,6) — элемент пространственного расстояния вдоль луча.
к получить и написать выражение ka 1 га с = га i 1 k i = g с ко 7 ко, + га. wi tk / s = -goc ^ -0- —- 7 os nv k7p, и Откуда Наконец, умножьте на dxa, чтобы получить принцип Ферма в виде коэффициент ujo / c опущен) Для статических полей просто Обратите внимание на то, что луч распространяется через гравитационное поле. Поскольку последний был решен, это не вдоль самой короткой линии пространства Уравнение 6 Ф дл = 0.
Смотрите также:
| Связь символов Кристоффеля с метрическим тензором | Вращение в физике |
| Движение частицы в гравитационном поле | Уравнения электродинамики при наличии гравитационного поля |

