Оглавление:











Координаты на плоскости и в пространстве
- Регулировка в плоскости и в пространстве /. Декартовы координаты на плоскости. Метод координат Как показано, положение точки на линии определяется одним числом (координатами точки). Положение точки на плоскости уже определяется двумя числами. в в L четверть I четверть \ «R m x <0; y> o x> o; y> o W четверть 0 IV четный l <0; y <0 x> 0; y <o X «1 4 и фиг.
На самом деле, на плоскости даны две взаимно перпендикулярные числовые оси Ox и Oy, имеющие общее начало координат O (совпадающее с пересечением осей) и единицу общего масштаба (рис. 4). Плоскость, на которой расположены оси Ox и Oy, называется координатной плоскостью и представляет собой Ox.
Рассмотрим произвольно выбранную точку M в координатной плоскости Оху и Mx Людмила Фирмаль
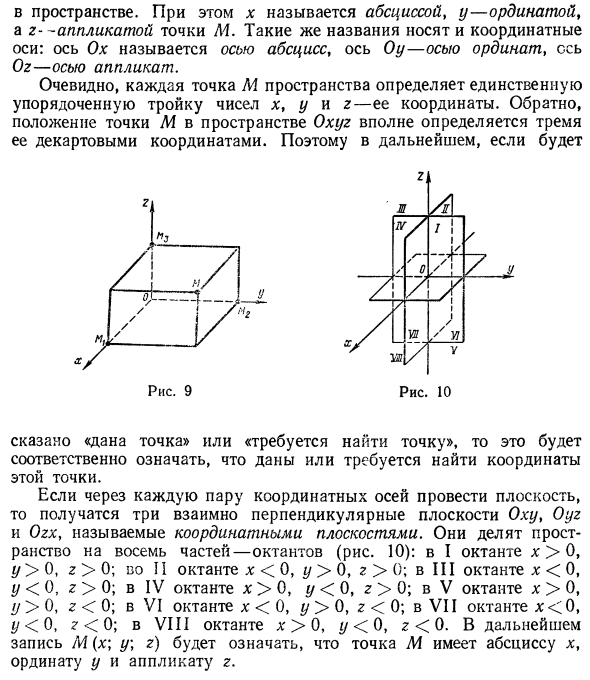
В космосе В этом случае x — абсцисса, y — ордината, а z — точка М. Оси имеют одно и то же имя. Ось Ox — это ось абсцисс, ось Oy — это ось ординат, а ось Oz — это ось ординат. Очевидно, что каждая точка M в пространстве определяет единственную упорядоченную тройку чисел x, y, z. Наоборот, местоположение точки M в пространстве Oxyz полностью определяется тремя декартовыми координатами.
Так что в будущем На рисунке 9 Рисунок 10 Если «заданная точка» или «нужно найти точку», это означает, что координаты этой точки заданы или должны быть найдены. Если плоскость проведена через каждую пару координатных осей, вы получите три плоскости Oxy, Oyz и Ozx, перпендикулярные друг другу, называемые координатной плоскостью. Разделите пространство на 8 частей — октант (рис. 10): 1-й октант x> 0, * /> (), 2> 0, 2-й октант x <0, y> 0, r> 0; III октант x <0, Y <0, r> 0; для четвертого октанта x> 0, y <0, r> 0; для октанта V: l:> 0, y> 0, r <0; VI Для октанта x <0, y> 0, r <0, для VII октанта, x <0, Y <0, r <0; VIII октант x> 0, y <0, r <0. В дальнейшем обозначение M (x; y \ r) означает, что точка M имеет абсциссу x% по ординате y и применяет r. г
| Вычисление длины дуги плоской кривой | Угол между двумя осями. полярные координаты |
| Действительные числа. координаты точки на прямой | Функциональная зависимость |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Расстояние между двумя точками в пространстве Многие геометрические проблемы могут быть решены с использованием пространственных и плоских координат. Рассмотрим один из них. Предположим, нам нужно найти расстояние между точкой M1 (x1 \ yx \ zx) и M2 (x2; y2; r2) в пространстве. Нарисуйте три плоскости, параллельные координатной плоскости, через каждую из точек Mg и M2 (рисунок 11). Эти шесть пересекающихся плоскостей образуют кубоид, диагонали которого — отрезки M и M2. Из стереометрии известен прямоугольный диагональный квадрат с параллелепипедом.
Равно сумме трех краевых квадратов, возникающих из одной вершины. так MXM \ = MXN% + MXR% + MXQ *. Спроектируйте концы параллелепипедных ребер MxNt MXR и MXQ по осям Ox, Oy и Oz соответственно и получите сегменты по этим осям. Кроме того, AVU CD и EF MXN = AB = | * s- * il> MxP-CD = \ y% -yx \ 9 MxQ = EF = \ z2-zx . Следовательно, квадрат искомого расстояния d d * = MxMl = \ xr — xx | 2 + или & = (Xi-xxu + {y, -ihu + + (R2-gx) \ Рисунок и, наконец, отсюда (В) d = V (x2-xxr + (y2-yxy + (z2-zx) \ Пример. Найти расстояние d между точкой Mx (–1; 2; –3) и AMI. 1; -5). Решения. Из уравнения (6) d =] / [l — (- l)] ‘+ (l-2)’ + [—5 — (- 3)] 2 = =] / Г2г + (-1) 2 -) — (- 2) 2 = 3
Координата x точки M на оси Ox называется абсциссой точки M, а координата точки Mg на оси Oy — ординатой точки M. Числа x и y, рассматриваемые вместе, называются прямоугольными (или декартовыми прямоугольными) координатами точки M. Очевидно, что каждая точка M на координатной плоскости соответствует одной упорядоченной паре чисел x и y, то есть ее декартовых координат.
Проекция точки M на оси M2 Ox и Oy. Людмила Фирмаль
Наоборот, каждая пара чисел x и y определяет уникальную точку M на плоскости Ohu. Фактически числа x и y соответствуют четко определенным точкам M и / 2 на осях Ox и Oy. Перпендикуляр к оси, сгенерированной в этих точках, пересекается с координатами хны в одной точке М. В будущем, когда вы говорите «дать точку» или «найти точку» на плоскости, это означает, что координаты этой точки задаются или требуются соответственно. Ось Ox называется горизонтальной осью, ось Oy является осью ординат, и обе оси Совместно-координатные оси.
Общее происхождение абсциссы и ординаты называется происхождением. Оси Ox и Oy делят координатную плоскость на четыре части, называемые четвертями (рис. 5). В первом квартале х> 0, у> 0. Во втором квартале x <0, y> 0, в третьем квартале x <0, y <0, в четвертом квартале x> 0, y <0. Я согласен написать M (x; y), где x — абсцисса, а y — ордината M. Например, обозначение M (1; -2) означает, что точка M имеет абсциссу 1 и ординату (-2). Пример.
Нарисуйте точку M на плоскости (5, 5; -2). Решения. Создайте точку Mx на оси координат M9 с осью абсцисс с координатой 5.5 и координатой (-2). Нарисуйте линию, перпендикулярную оси Ox, проходящей через точку Mt, и линию, перпендикулярную оси Oy, проходящей через точку M2. Точка M на пересечении этих линий является точкой интереса (рис. 6). в 0 мл (3,5) х М (5,5 г 2) Рис. 6
Поэтому положение точки на плоскости определяется упорядоченной парой чисел, то есть координатами этой точки. Ниже вы можете видеть, что положение точки в пространстве определяется тремя числами. Метод использования числовых значений для определения положения точки называется методом координат.
Автором метода координат является французский математик Декарт, который применил этот метод ко многим геометрическим задачам и разработал новую геометрию, аналитическую геометрию, чтобы изучать характеристики геометрических фигур и их взаимное расположение алгебраическими методами. Она была создана. Простейшими проблемами с аналитической геометрией являются разделы 2, 3,
4 и 5. Основные разделы анализа геометрии описаны в главе 4. II и IV. В дальнейшем методы координат были широко разработаны и применены во многих областях математики и механики. В следующем параграфе мы рассмотрим применение метода координат для решения некоторых геометрических задач. 2. Расстояние между двумя точками на плоскости Дайте две точки: Mx (xx; yx) и M2 (x2; y2). Надо найти расстояние между ними.
Сначала предположим, что сегмент MXM2 не параллелен ни одному сегменту Out! Координатные оси (рисунок 7). Нарисуйте прямую линию через точку Mx, параллельную оси Ox, нарисуйте прямую линию через точку M2, параллельную оси Ox, и отметьте точку N на пересечении этих линий. Треугольник MXM2N представляет собой прямоугольник. По теореме Пифагора MiMl ^ M ^ + NMl Пусть A и B — проекции на точку Mx и ось Ox на рис. 7 M2, а C и D — их проекции. Та же точка на оси Oy. MXN = AB ^ \ xr-x11; NM2 = CD = \ y2 — yy |.
Требуемое расстояние MXM2 выражается как d следующим образом. d2 = | I2 +1 Y, -Y y | 2 = (x2-xxu + (yx-yy) \ так d = V (x2-xx) * + (y2-yx) \ (2) В частности, расстояние d точки M (x \ y) от начала координат можно получить по следующей формуле. d ^ V & Ty *. (3) Уравнение (2) остается в силе, если сегмент MXM2 параллелен одной из осей. Пример. Найти расстояние между точкой Mx (2; -I) и M2 (-1; 3). Решения. Из уравнения (2)d = * V (–1–2) a + [3 — (- 1)] 2 = 5. 3. Сегментация в этом отношении Чтобы разделить сегмент MXM% в этой точке, X> 0, что означает нахождение точки M, в которой выполняется уравнение в данном сегменте. да
Предположим, что координаты точек M1 и M2 равны xX9 yx и x% 9 y2 соответственно. Найти координату х в точке М. NxtN и N2 показывают проекции точек Mx, M и M2 на ось Ox (рис. 8). Из базовой геометрии видно, что сегменты, окруженные параллельными линиями, пропорциональны. так MXM_NXN_ * MM2 ~ NN2 • Однако NXN = | x-xx |, NNi = \ x2-x \, поэтому ‘x! = Я здесь Я х я Монтажный модуль является сменным x% -x, учитывая, что эти различия имеют один и тот же знак (см. фиг. 8a, где оба различия положительные, и фиг. 8.6, где они отрицательные).
Вот так х — х 1- = Х. х «—х Отсюда * 1 + X-DG2 1 + X Точно так же вы можете получить выражение, соответствующее y. Наконец, получите следующую формулу для координат x и y желаемой точки M: и x2 — x {X — chl X — X разница Рисунок 8 х = xy + \ x2 Y = 1 + X Y + тыт 1 + Х
В частности, координаты средней точки отрезка = Выражение получается: + 2 (5) в Вау ~~ Таким образом, каждая координата в центре сегмента равна среднему арифметическому соответствующих координат на его концах. Пример. Разделить сегмент MtM%, если AMI 2), AM3; 4). 2 Решения. Поскольку x, -1, * / x = 2, -3 и =, из уравнения (4): ‘+ T3_5, I 3 1 + Т 2 + T’4 8 деления точек относительно X = y имеет начало M2 (3; 4) и конец M (1; 2) и больше не является точкой M. И точка M (x; y), ее координаты: -3 + Т- ‘7 -4 + f2 10 V = —r = m- 1 + Т 4. Координаты в пространстве тонкие Указывает, что положение точки в пространстве может быть определено тремя числами.
Рассмотрим три оси, которые ортогональны друг другу в пространстве Oxt Oy и Og. Он имеет общую начальную точку O (пересечение оси) и общую единицу шкалы (рисунок 9). Эти оси называются координатными осями, и их общее начало — это начало и координаты. Пространство, в котором определены оси Ox, Oy и Og, обозначено Oxtjz. Пусть M — точка, произвольно выбранная в пространстве Oxyz. Нарисуйте три плоскости, перпендикулярные осям. Точки Mlf Ma и M3 на пересечении этих плоскостей с осями Ox, Oy и Oz называются проекцией точки M на соответствующую ось. Предположим, что точка Mx на оси Ox имеет координату x, точку M.g на оси Oy — координата y и точку Mi — r на оси Og.

