Оглавление:


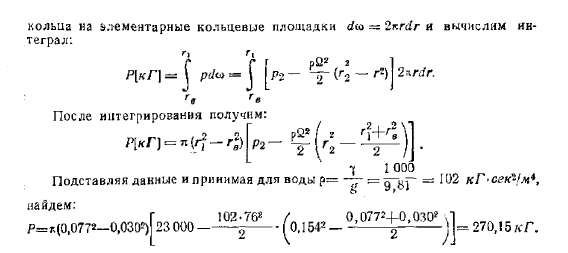

Относительный покой жидкости, находящейся в резервуаре, вращающемся вокруг горизонтальной оси
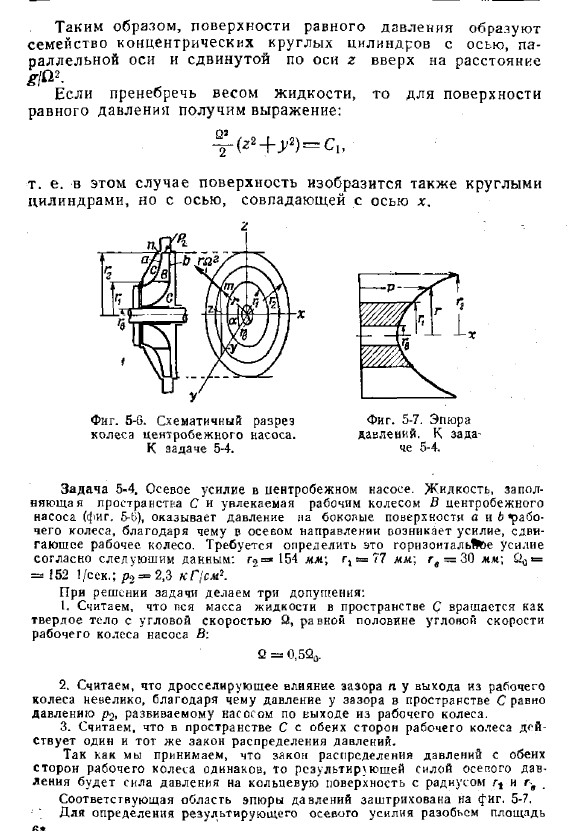
Относительный покой жидкости, находящейся в резервуаре, вращающемся вокруг горизонтальной оси. Например, расследуемое дело Осевое усилие центробежного насоса (рис. 5-6 Жидкость для заполнения корпуса боковым пространством c считается, что ЦС вращается как твердое тело. Относительно мирно. Найти и заполнить закон распределения давления в жидкости.
Смотрите также:
Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Людмила Фирмаль
Пространство c. Для этой цели используйте diffe Уравнение потенциала (5-1). Рассмотрим некоторые частицы На расстоянии r от оси вращения и радиус? Н. Вращение образуя ось y и угол a: $ xyh + yyu + 2yy) = yr Где x, y, 2-проекции на ось координат ускорения равного узла Объемная сила, в данном случае Сила тяжести и центробежная инерция Движение. Найдите проекцию на координатной оси. Х.
Смотрите также:
Поскольку gsoza-y и r равны 51 pa-g, y и r относительны. Координаты, значит Присвоить эти значения дифференциальному уравнению, бу Есть Дем: УГ = р [О. 2 (гыг + г г г Если вы консолидируетесь, вы найдете закон распределения давления. р = р [^ р (22+ г 2) е р] + с. При пренебрежении законами расы, влияние веса жидкости Распределение давления p получает следующее уравнение: р = р ^ (Р3 + ^) + с Или 0 * г * Р = + с.
Интегральная постоянная c определяется давлением p2>. Развитый насосом когда жидкость приходит из работая Кола ЦС на окружности с радиусом r2. Предполагая r = r2 и p ^ p, вы можете увидеть следующее: т С = Р2 П «» Н— Итак закон распределения давления Следующая формула: Это выражение является Рисунок 2: 5-7. Поверхность давления представляет собой параболоид Ось совпадает с осью вращения (валом) насоса.
Смотрите также:
В заключение определите поверхность равного давления. Для этого используйте формулу (5-2). Замена. Добавьте к нему значение x> v7 2 и запустите интеграцию. Получаем уравнение поверхности равного давления. ^ (Р2 + В2) & = С Это уравнение можно свести к следующему виду: Ык + [*б) ‘ с>§ 6-4] остальная жидкость во вращающемся резервуаре 83 Таким образом, образуется поверхность равного давления Семейство концентрических круглых цилиндров с осями.
Переместите расстояние вдоль оси z на оси, параллельной ^ / Р2. Игнорируя вес жидкости, поверхность будет Получаем уравнение с равным давлением: * (r * + y>) = c иТо есть в этом случае поверхность также будет закругленной Цилиндр, однако, имеет ось, которая совпадает с осью x. Рисунок * 5-6 * принципиальная схема Колесо центробежного насоса. К выпуску 5-4. И фигура тоже. 5-7. Сюжет pressure.
При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Людмила Фирмаль
- Жидкостная завалка Увлекается космическим инкубатором и центробежным рабочим колесом в Насос (рисунок 5-6), надавите на стороны а и в работы Колесо смещается за счет наличия осевых сил Горение impeller. It необходимо определить эту горизонтальную силу По следующим данным: r2 = * 154 мм r1 = 7 7 мм; guard-30 dde; &0> = = 152 1 / С; от g (см2). При решении задачи сделайте 3 предположения.
Общая масса жидкости в пространстве С равна Твердое тело с угловой скоростью, равной половине угловой скорости Крыльчатка насоса Б: Дж = 0 .520 .2 .Тормозящее действие зазора l на выходе рабочих Поскольку колесо мало, давление зазора в пространстве C Давление, создаваемое насосом на выходе из рабочего колеса/> 2> .3 .In пространство C с обеих сторон крыльчатки Действует закон такого же распределения давления .
Потому что мы принимаем закон распределения давления от Стороны турбинки эти же и приводя к осевая сила Давление на кольцевую поверхность радиусом r *и ГД Соответствующая область графика давления заштрихована на рисунке 3 .5-7 .Разделите площадь, чтобы определить результирующую осевую силу 6 .* 84 .основа теории плавания[гл . 5 .Кольцо основное кольцо коврик.

