Оглавление:





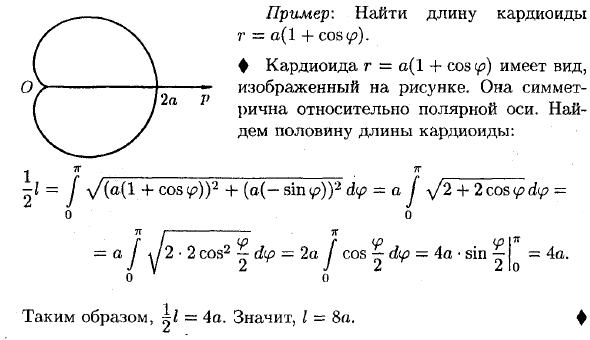
Вычисление длины дуги плоской кривой
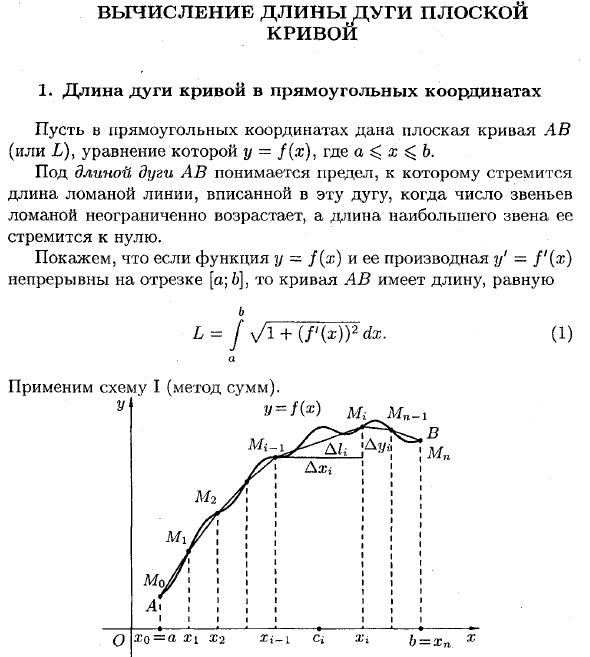
- Расчет длины дуги кривая I. Длина дуги кривой в декартовых координатах Предположим, что плоская кривая A B (или L) задана в декартовых координатах, где уравнение имеет вид y = f (x). Где а <х <б. Длина дуги ЛВ означает предел длины пунктирной линии, вписанной в эту дугу, когда число пунктирных звеньев увеличивается бесконечно, а максимальная длина звена стремится к нулю. Функция y = f (x) и ее производная y ‘= f’ (x) находятся в интервале [a; 6], а длина кривой AB равна b _ L = j 0 (/ ‘(*)) 2 <fe. (1) о
Разделите π-сегмент в точках X0 = a, x1, …, xn = 6 (x0 <x1 <•• <xn). Рисуем аккорды MqM \, Mi Mo y …, Mn-iMn. Его длина обозначается как D / i, D / 2 соответственно 2. •••, A ^ n. Получить пунктирную линию MqMtMi … Mn-iMn, длина N / n = D / i 4-D / -2 равно + + •• + A 1n = «= Я 2. Длина хорды (или разорванной связи) AU — теорема Пифагора, фут катакс и / = y / (Axi) 2+ (Du, -) 2, Dxr = x, -D </ r = f (si) — / (* <-i) -конечный приращение функции по теореме Лагранжа
Предположим, что эти точки соответствуют точкам Mo = A, Mi, …, Mn = B на кривой A B. Людмила Фирмаль
W 0 (<(u <-i (r <). Следовательно, D ( 1 1 = 1 .’J. Кривая JlHMIIft £, по определению, равна L = 1 | m / n = Тля W <* hO = llin A /, -. D / j-> 0, DX (0 Шикарный D <| «+0 ги (Alj € y / (Axj) 2 + (& yr) 2, таким образом | Dx; | 0, существует предел на интегральную сумму (2). 71 L = Jsu Y. V1 + (/ ‘fa)) 8 = / yrrifw «fa. (P- ♦ DO) i = l 6 Следовательно, L = \ / l + (f ‘(x)) 2 dx или сокращенное обозначение b a I> / 1 + (s) 2L? , но Когда уравнение кривой задано в параметрической форме * = т! ‘»<* <A Где r (/.) И i / (f) — непрерывная производная, а x ((y) -a, x (непрерывная функция (1) = by)), а длина L кривой AB равна По подсказке P L ^ fy / Schu ^ TWWdt. (3) но
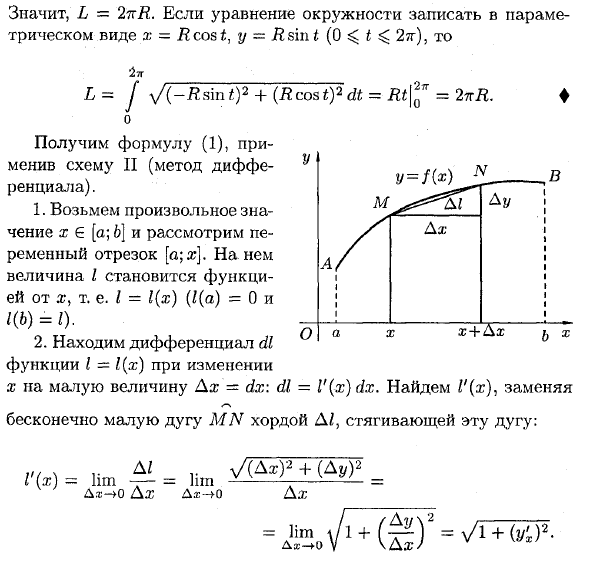
Уравнение (3) может быть получено путем подстановки x = x (t), dx = x ‘(t) dt,} \ x) = uting из уравнения (1). Пример: Найти окружность радиуса L. ♦ найти я часть s.c. Длина от точки (0; R) A A A К. Дж * 1 + R х 7G o = DT Очки (7?; 0). Поскольку y = y / R2-x2, X * f) -dx = I-arc sin-R2 ~ xl R Следовательно, L = 2tr #. Круговое уравнение имеет параметрическую форму x = Roost, y = i? Если написано в Синт (0 ^ £ ^ 2г), ■ 2л L = ■ Jy / (-Rsmt) 2+ (RcosО2dt = Rt \ 2Qn = 2tL. ♦ о Примените Схему II (дифференциальный метод), чтобы получить уравнение (1). 1.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Произвольное значение x e [a; 6] Сегмент переменной [a; x]. Тогда величина / является функцией от x, т.е. / = l (x) (1 (a) = 0 и 1 (b) = 1). 2. Найти производную dl функции I = 1 (x), когда x изменяется на небольшую величину Ax = dx: dl = l ‘(x) dx. найти l ‘(x) и заменить Минимальная дуга MN с кодом D / сжать эту дугу: = ШпУпНет. + ™ = Ах-> 0 Ах LA- + 0 Ах У-правильно) * _B м ^^ Y \ 1 1 1 1 Ач o a x f + dy b x
дх но Уравнение dl = yl + 2 / i-2 ^ называется дифференциальной формулой дуги в декартовых координатах. ух = тогда в о хорошо но Последнее уравнение является теоремой Пифагора для бесконечно малого треугольника MCT.
Следовательно, dl = yj \ + (y’x) 2dx. 3. дл интеграции с О — 6, получить L = / WL + Y’X2 Людмила Фирмаль
Длина припойной дуги I полярных координат LI кривая ttuiAmm согласно уравнению полярных координат r = r (sp) y a Параметр координаты Yay, рассмотрим угол кривой } X = G (если) спящий IP, ^ // Вы можете установить ^ с параметрами. Goguda [2 / = г (^) грех ^. x’v = r ‘(y?) cos (/ 7-r (tp) sin v?, * / £> = r’ (tp) sin ) sin y>) 2+ (r’ (y>) sin + r (<p) cos un) 2 = Используйте уравнение 3, чтобы получить: I = J y / r2 + r’2dtp.
Пример: Найти длину кардиоида r = a (1 -f cos f). ♦ Формат кардиоиды r = a (14-cosc ^) показан на рисунке. Симметричный относительно полярной оси. Найдите половину длины кардиоида: ^ <«/ I -I = J \ / (a (\ 4-cosv?)) 2 4- (о (-sinу?)) 2 dip = aj \ J2 4-2 c.os ipd \ p = = 4а. ♦ = o J J 2 • 2 cos2 ~ dtp = 2a J cos ^ = 4a Следовательно = 4а. Поэтому я = 8а.

