Сравнение двух средних

Сравнение двух средних

• Сравните два средства При анализе часто необходимо сравнивать два или более средних значения. Это происходит, например, когда один и тот же образец анализируется по-разному. В таких случаях важно проверить, является ли разница в результатах статистически значимой. Рассматривая эту проблему, они сначала выясняют, насколько важна дисперсия сравниваемых значений.

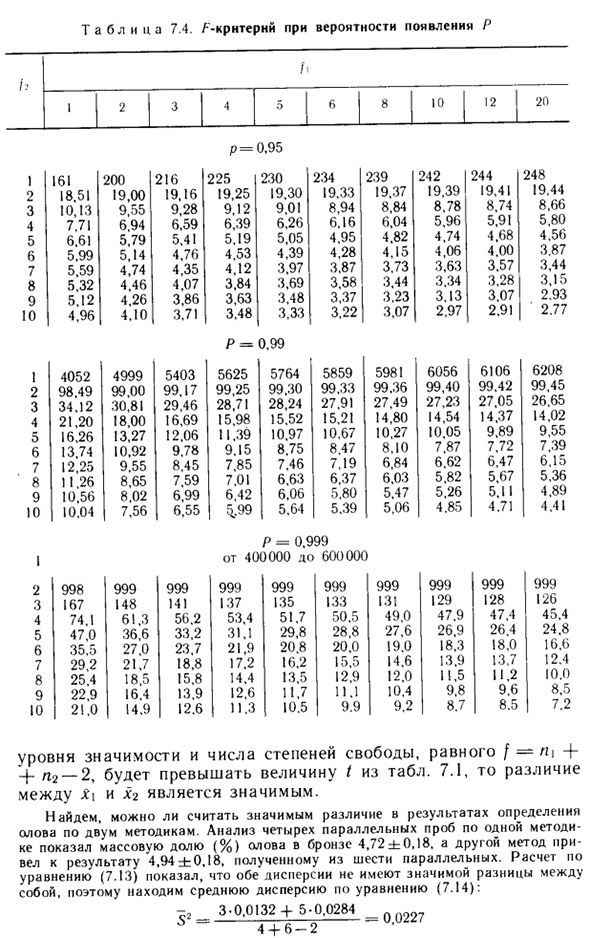
• Проверка является / — «Стандарт: F = Si / Sl (7,13) Где Sj — максимальная дисперсия. Поскольку Si маленький, эталон F всегда больше 1. В таблице. 7.4 ^ Числа критериев даны для разных вероятностей возникновения и разных степеней свободы. Если F-критерий, рассчитанный в соотношении (7.13), превышает значение в таблице (F1 abl) для заданной вероятности и количества степеней свободы, существует значительная разница между дисперсиями.

Например, серия анализов с четырьмя измерениями дает содержание олова в бронзе с дисперсией 0,0132 и еще одну серию из 6 параллельных дисперсий с другой серией 0,0284, 0,0284 0,0132 Людмила Фирмаль

Согласно таблице, если 7,4 fi = 5, / 2 = 3, P = 0,99, значение критерия F составляет Fo & .ss = 28,24 и P = 0,95 F0,95; 5; s = 9,01 , , Следовательно, даже на уровне значимости 5% разница в значении отклонения невелика, поэтому оба значения должны принадлежать одной и той же выборке. Если критерий F показал, что разница в дисперсии значительна, средние значения для X1 и x2 нельзя сравнивать друг с другом.

Если есть небольшая разница в дисперсии, найдите средневзвешенную дисперсию. -52_ («■ -«) $. + (I * — ) Sj I | + L} -2 Затем вычислите ссылку t. / = JfLZLiil £ _. (7,15) VS2 + 12 Когда значение / находится в определенном выражении (7.15) (7,14) Число степеней свободы, равное уровню значимости и / = n \ + + n <2 -2, превышает значение t в таблице. 7.1, отличие от х \ важно. Давайте рассмотрим, можно ли считать существенной разницу между результатами измерения олова двумя методами.

Анализ четырех параллельных образцов одним методом показал массовую долю бронзового олова (%) 4,72 ± 0,18. Другой метод дал результат 4,94 ± 0,18 из четырех параллельных результатов. Расчет в уравнении (7.13) показывает, что обе дисперсии существенно не отличаются, поэтому средняя дисперсия определяется в соответствии с уравнением (7.14). -2 _ 3-0.0132 + 5.0.0284 _ Л-4 + 6-2

Далее рассчитайте коэффициент t, используя соотношение (7.15). 0,151 Y 4 + 6 Сравнение с таблицей. В 7.1 f0. Won; b = 2,31, то есть>, поэтому между этими двумя результатами нет существенной разницы. Если средний результат независимой серии независимых определений одного и того же компонента различными методами или разными аналитиками немного отличается и характеризуется различными ошибками, наиболее вероятными значениями являются критерий F для ошибки и результат / критерии.

Средневзвешенное значение всех результатов, которые удовлетворяют «Вес» o) каждого результата является своего рода уверенностью в результате. Очевидно, что чем меньше ошибка в результате, тем больше «вес» при расчете средневзвешенного значения. о> значение можно рассчитать по соотношению По определению 6 (7.6) является наиболее вероятной ошибкой в ​​анализе.

Средневзвешенное значение определяется по формуле -Jt | 0> i + LG20> 2 + … (7,16) (1) 1 -} — (1) 2 + … + Более удобно выполнять фактический расчет с небольшим изменением отношения, а не напрямую по уравнению (7.16). hi-L | (* ‘~ + ~ L) 0) 2 + (* n-A) f) | + W2 + … + tOrt Здесь, как показано в уравнении (7.7), Л — произвольно выбранная величина, и исходное положение отсчета смещается на нее для удобства расчета.

Обычно это округленное значение, близкое к среднему. Ошибка средневзвешенного значения 6W выглядит следующим образом 6W == y — r ———; — r = ‘0) 1 + (1) 3 + … + (1) n Найти средневзвешенное значение и его ошибку при получении трех результатов анализа (%): 4,72 ± 0,18; 4,94 ± 0,18 и 4,87 ± 0,14. При расчете по формуле (7.17) 4.80 можно принять за А. ~ 0 08 (г-н + 014 (г-н + 0,07 (млн. X,. , = 4,80 Н-д — 1 ——— 4,85; (Oje) + (oL8) + (oGi)

Задача 1. Измерение содержания свинца в сплаве дало следующие результаты (%): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,19. Оцените наличие общей ошибки и рассчитайте среднее значение и доверительный интервал. Наличие общей ошибки оценивается по критерию Q.

Существуют экспериментальные данные с увеличивающимися числами: 14,25; 14,40; 14,43; 14,44; 14,45; 14,49; 14,50; 14,52; 14,54; Предполагается, что значения 14,25 и 14,58 являются результатом общей ошибки. Рассчитайте Q базис для этих величин. L _ 14,40 -14,25 0,15 = 0> 45; 14,58 -14,25 0,33 14,58-14,54 0,04 = 0,12 14,58 -14,25 0,33 Для P = 0,95 и n = 10 табличное значение Q = 0,42. Q > 0,42 Поэтому значение C \ = 14,25 считается ненадежным и исключается из числа статистически обработанных количеств.

В измерении Сю = 14,58, Qi <0,42, поэтому большой ошибки нет. Вычислите среднее арифметическое из девяти определений. 14.40 + 14.43 + 14.44 + 14.45 + 14.49 + 14.50 + 14.52 + 14.54 4-14.58 секунд- 9 = 14,48. Найдите стандартное отклонение: (0,08) 2+ (0,05) 2+ (0,04) г + (0,03 / + (0,01) 2+ (0,02) 2+ (0,04) * + L ~ ~ Y Q-I ± W £ ± W1— 5.82.10-9-1 Стандартное отклонение среднего результата выглядит следующим образом: 5.82..0 ‘= 94. | 0, г V9 L Доверительные интервалы рассчитываются, но используйте вкладки.

7.1. tp f = 2,3! (I = 0,95; I = 9-1 = 8): tpjS {= 2,31 • 1,94 • 1 (H = 4,48-10 «2. Опять же, оцените наличие общей ошибки в соответствии с критерием 35. 35 = 3-5,82-1 (Гг = 0,17. Сравнивая значения (s, -s) с 35 = 0,17, отклонение от среднего никогда не превышает 35. Следовательно, значение c не включает общую ошибку.

• Среднее значение результата анализа отведений при P = 0,95 определяется доверительным интервалом (14,48 ± 0,04)%. Результат решения должен быть выражен как число с двумя значащими цифрами после десятичной точки, чтобы соответствовать точности полученного анализа. 2. Анализ стандартного образца, содержащего 1,47% Ag, дал следующие результаты (%): 1,31; 1,45; 1,42; 1,32; 1,30.

Определите стандартные отклонения, доверительные интервалы и сделайте выводы о возможных систематических ошибках в методе определения серебра. Найти среднее арифметическое. 1,31 + 1,45 + 1,42 + 1,32 + 1,30 = 1,36. 5 Рассчитайте стандартное отклонение. s = (0,05) * + (0,09) 2 + (0,06) ‘+ (0,04) 2 + (0,06 / =% 5-1 Согласно таблице, для P = 0,95 и f = 5 — 1 = 4, 7,1, используйте //> ./ = 2,78, чтобы вычислить доверительный интервал для значения. s ± tP_, S / ^ n = 1,36 ± 2,78-fr96 ^ 0 * = 1,36 ± 0,09 V5

Истинное значение содержания серебра не попадает в доверительный интервал. Людмила Фирмаль

Следовательно, существуют систематические ошибки в этом методе определения серебра. 3. При определении массовой доли (%) серы в угле определите, есть ли значительная разница в среднем значении образца. 2,12; 2,13; 2,15; 2,15 и средняя численность населения, l = 80 q = 2,15%. Среднее значение выборки — ^ 2,10 + 2,12 + 2,13 + 2,15 + 2,15 = 2, 3 5 Стандартное отклонение для каждого определения: 0,032 + 0,012 + 0,002 + 0,022 + 0,02 5-1

Найти значение т. (2,15-2,13) ​​-1 / 5 _oll / = -2,12-10 * -2-1L В таблице коэффициентов Стьюдента (см. Таблицу 7.1) для / = 4 и P = 0,95 дано / # \ ./ = 2,78, что превышает расчетное значение. Следовательно, среднее значение c не очень отличается от среднего значения q всего населения. 4. Измерение ванадия дало следующие результаты: 8,00-10 4; 8,40-U-4. Что такое доверительный интервал? 10 = 2,12-U-2.

Сколько параллельных измерений требуется для достижения доверительного интервала ± 0,41 «S-4? Оправдано ли применение этого метода для достижения такого доверительного интервала? Найти среднее значение: 8.00-10 ‘+ 8.40-10-1 = 820., 0- < Стандартное отклонение для одного результата: S- = 0,283,10- «. Согласно таблице, если 7.1 P = 0,95 и f— \, tPJ = 12,7. Вычислить доверительные интервалы: = 12,7 ± 2v32 ‘°’ <-2,54-10 ~ ‘. -4.

Требуется доверительный интервал ± 0,41 * 10. 0,41 • \ 0 ~ A- \ Jn 0,283,10- ‘ Для n = 4, / = 2,90, согласно таблице. 7.1. Для P ~ 0,95 и / = 4-1 = 3 tPJ = 3,18 не обеспечивает определенный доверительный интервал с вероятностью P = 0,95. Для n = 5 / = 1,45 V5 = 3,24. Согласно таблице, 7.1 | m-P = 0,95 и / = 5-1 = 4 2,78 меньше, чем рассчитанное / = 3,24. Таким образом, для n = 5 значение / = 3,24 дает вероятность больше 0,95.

Поэтому для достижения доверительного интервала ± 0,41 * 10 «» * требуется 5 параллельных измерений. Поскольку n <8 (n = 5), можно предположить, что этот метод достаточно оправдан для достижения такой точности. 5. Массовая доля (%) CuO в минералах определялась методами йодометрии и комплексометрии. Согласно первому способу, результат таков: 38,00; 37,66.

Второй 37.70. 37,65; 37,55. Будут ли результаты этих методов значительно отличаться? Рассчитайте среднее значение для каждого метода. -38,20 + 38,00 + 37,66-37,70 + 37,65 + 37,55 „s | —- = 37,95; c2 = — = 37,63. Рассчитать дисперсию: S2 = (38,20-37,95) * + (38,00-37,95) * + (37,66-37,95) » = Q ()? 453 $ = (37,90-37,63) * + (37,65-37,63) * + (37,55-37,63) * = () ^^ 3 * — * 1

Сравните точность обоих методов с использованием F-распределения: _S] _0.07453_g, .с 0,00583 ~ A Полученное значение F cn сравнивается со значениями в таблице распределения F (см. Таблицу 7.4) при P = 0,95 и количестве степеней свободы /, = 2 и / g-2. ^ 0.95.2.2 = I9.00 и более поздние> FyK „, есть небольшое расхождение между дисперсиями, поэтому точность метода одинакова.

Оценить несоответствие c1 и cn, используя / критерии. Средневзвешенное значение двух дисперсий рассчитывается по формуле _ (L | -1) 5? + (L? -I) S3 _ 2-0.07453 + 2-0.00583 / -s «‘в s * l / n * n * 37’95- 🙂 7,63 л / 3-3 , ^ tm «» «TK7» K + * V0.04018 Y ~ 3 + T-I, Jb Сравните полученное значение f> «„ с табличной формой f0.9s.4 = 2776 (P = 0,95 и / = 3 + 3-2 = 4) из / „Cr << 0,95,4.

Разница между c (и c2) незначительна, поэтому все результаты обоих методов отражают истинное содержание CuO в минерале. Поэтому аналитические данные могут отображаться как: c ± tp. , S / -y] n, Где c — среднее арифметическое всех результатов ni + Pg. с = 38,20 + 38,00 + 37,66 + 37,70 + 37,65 + 37,55 = 3? ^ 5 = ода. ^ ^ Результат анализа: (37,79 ± 0,26)%.

Смотрите также:

Решение задач по аналитической химии

Погрешность суммы и произведения	Сущность гравиметрического анализа
Обнаружение промахов	Форма осаждения