Оглавление:



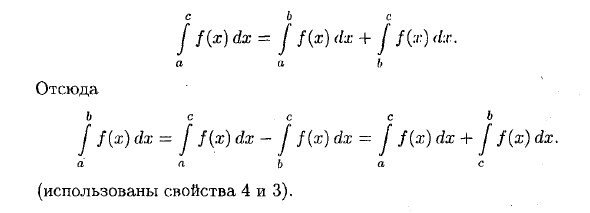
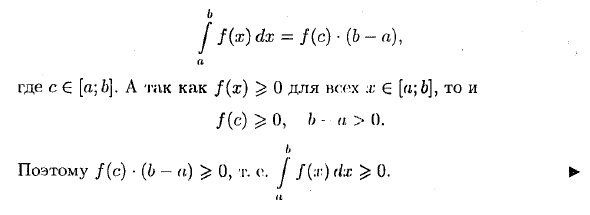



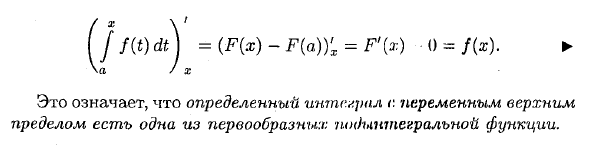
Основные свойства определенного интеграла
- Основные характеристики определены интеграл Рассмотрим основные свойства конкретного интегрирования, принимая во внимание, что подынтегральное выражение может быть интегрировано за интервал [a;. Б]. При выводе свойств используются интегральные определения и уравнения Ньютона-Лейбница. 1. Если c постоянная и функция f (x) интегрируема с [a; b], б б J c-f (x) dx = c-f f (x) dx, (1) а То есть постоянный коэффициент c может быть извлечен из знака конкретного интеграла.
■У нас есть: N я = я я = 1 б 71 II A Тогда lim J2 c ′ / (x) J * = c-lim £ f (ci) = • c • / f (x) dx. Отсюда «- + oo ri—> oo j J Следовательно, функция c-f (x) может быть интегрирована с [a;. 6] и уравнение (1) выполнено. ► 2. Если функции fi (x) и f2 (x) интегрируемы с (a; 6], их сумма равна [a; b] и b b b f (fi (x) + f2 (x)) dx = J h (x) dx + f Mx) dx, (2)
Создает интегральную сумму четырех функций c • f (x). Людмила Фирмаль
Jf (t) dt \ = (F (x) -F (a)) ‘x = F’ (x) 0 = f (x) ► ва / х Это означает, что определенный интеграл r с переменным верхним пределом является одной из обратных производных подынтегрального выражения.То есть полный интеграл равен общему интегралу. 6 р <[(A (*) + f2 (x)) dx = lim T (fy (ci) + / 2 (c)) D * <= «/ Tl-> oO рт т = л 71 n 6 & = lim] P / i (ci) Aa: t + lim Mb) Ax {= [fi (x) dx + [f2 (x) dx. ► n—> oo z — 4 n- »ooz— ‘J J я = 1 цаля
Свойство 2 распространяется на сумму любого конечного числа Срок действия. 6 3. j f (x) dx = -J} {x) dx. а б Это свойство можно получить по определению. Это свойство также подтверждено формулой Ньютона-Лейбница. б f J (x) dx = F (b) -F (a) = — (F (a) -F (b)) = -J} {x) dx. а 4. Свойство аддитивности. Функция f (x) равна [a; 6] и oo (d-> 0), дает уравнение (3). ► Свойство 4 действительно для любого размещения точек a, 6 и c (при условии, что функция f (x) может быть интегрирована по большему из результирующих сегментов). Так, например, если <b <c
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
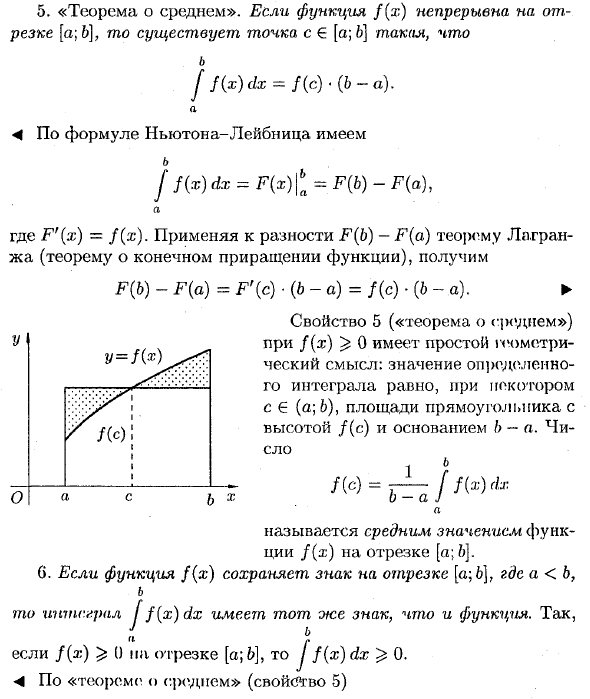
- J f (x) dx = J f (x) dx + J f (x) dx а (* б Отсюда б с с с J f (x) dx = J f (x) dx- I f (x) dx = J f (x) dx + a a b a (Свойства 4 и 3 используются). «Средняя теорема». Функция f (x) находится в интервале [a; B], точка c € [a; B] такая f f (x) dx = № .- (6-а). L • 4 формулы Ньютона Лейбница, 6 Где F ′ (x) = f (x−). Применяя теорему Лагранжа (теорему конечного приращения) к разности F (b) -F (a), F (6) -F (a) = F ′ (c) (b-a) = / (s) • (6-a). ► Свойство 5 («средняя теорема») с f (x)> 0 имеет простой геометрический смысл: значение определенного интеграла равно G (a; b) и высоте f (c)
Для G.φ ()) функция f (x) сохраняет знак интервала [a; b]. Где а <б, б Интеграл J f (x) dx имеет тот же знак, что и функция. так Если интервал [a; f (x)> 0 6], то J f (x) dx ^ 0. <«Теорема о среднем значении» (свойство 5)
Он равен прямоугольной площади нижней части ба. номер м ^ Jm! , но Оно называется средним значением функции f (x) на интервале [a \ b]. Людмила Фирмаль
б f f (x) dx = f (c) • (b-a), Где с € [а; 6]. И для каждого x € [a; f (x) ^ 0 6], то / (C) ^ 0, b-a> 0. Я Следовательно, f (c). (6-а)> 0, то есть J f (x) dx ^ 0. ► Неравенства между непрерывными функциями на отрезках [o; 6], (a 0 или позже, если б J t dx ^ J f (x) dx ^ J M dx. а р а Применение свойства 5 к экстремальной интеграции,
час м (б-а) ^ J ф Если f (x)> 0, свойство 8 показано геометрически. Изогнутая трапециевидная область заключена между прямоугольными областями, ее основание [«; &], а ее высота равна m и M. х) дхММ (ф; -а). ►Конкретный модуль интеграции не превосходит интеграцию модуля интеграции: О В I f (x) dx ^ J \ f (x) \ dx \ a <b. Но о <4 Применим свойство 7 к очевидным неравенствам- | / (j 🙂 | ^ f (x) ^ ^ \ f (x) \, получим б б -J \ f (x) \ dx ^ J f (x) dx ^ J \ f (x) \ dx а В сопровождении J f (x) dx J \ f (x) \ dx. а 10. Производная конкретного интеграла no по верхнему пределу переменной равна подынтегральному выражению, интегральная переменная которого заменяется этим пределом. Это значит Jf (t) dt) = f (x). X * J f (t) dt = F (t) \ l = F (x) -F (a) так

