Оглавление:

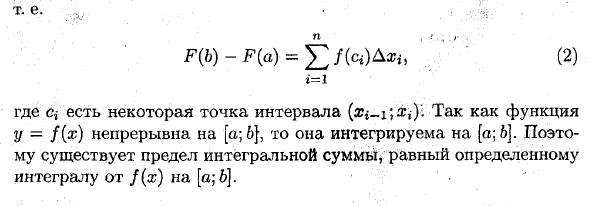

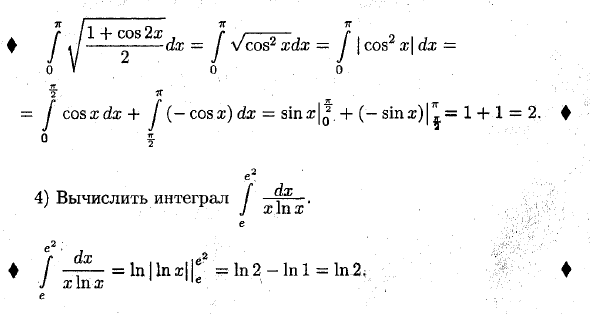
Связь определенного интеграла с неопределенным (формула Ньютона-Лейбница)
- Связь между определенным интегралом и неопределенностью (формула Ньютона Лейбница) Предположим, что φ ^ 1 $ $ © y = f (x) можно интегрировать по интервалу [a; b]. Теория Дня! Для функции у. f (x) — это интервал [a; 6], а F (x) 4 ^ — это [a; b] (F ‘{x) = f (x)), есть выражение. .vl-i b -G » [f (x) da F F (b) -F (a). (1) И д *
«Разделите сегмент [a; 6] n частичных сегментов [x0; точки a = x0, X1, …, b = xn (x0 <s1 <••••• <xn) x ], [X \ xr], …, [xn_ i; hp]. Cl C2 C, «Cn x -1-1 —.— | — • — (—.— | —..— | —-— | — • -I —.— I— • — | — О a = xo xi X2 Xi_ 1 Xi b-Xn Рассмотреть идентичность F (b) -F (a) = F (xn) -F (x0) = (F (xn) -F (z „-i)) — (F (xn_i) -F (x„ _2)) + ■ •• + (F (x2) -F (α,)) + №) — F (x0)). (/ () — / (a) = / ‘(c) • (6-a)). получить F (b) -F (a) = F ‘(Cn) • (a? „+ F, (cn.1) • (s„ -i-xn_2) +, — « n P ,. • + F ‘(c2) — (x2-X!) + F’ (ci) (X! -X0) = Axi Axi = ДAx® я = 1 т = 1
Преобразуйте каждую разницу в скобки согласно формуле Лагранжа Людмила Фирмаль
| Определенный интеграл как предел интегральной суммы | Основные свойства определенного интеграла |
| Геометрический и физической смысл определенного интеграла | Вычисление определенного интеграла |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- F (b) -F (a) = £ / (<*) Dach, t = i Где Cj — некоторая точка интервала. y = f (x) непрерывно с [a;. 6} то есть [a; 6]. Таким образом, существует предел интегральной суммы, равный конкретному интегралу функции f (x) в [a; 6]. Равенство (2) Л = max 0, половина Чай ■ ‘x’- N F (b) -F (a) = Urn V f (a) Дача, т. Е. F (b) -F (a) = [f (x) dx. ► .g, -a
Уравнение (1) называется формулой Ньютона Лейбница. Когда мы введем обозначение F (b) -F (a) =, New Тон Лейбница (1) б J f (x) dx = F (z) \ ba. но Формула Ньютона Лейбница обеспечивает удобный способ вычисления конкретного интеграла. Чтобы вычислить конкретный интеграл от непрерывной функции f (x) в интервале [a; 6], нам нужно найти ее обратную производную функцию F (x) и взять разность значений F (b) -F (a) Есть Это антипроизводное на обоих концах сегмента [a; B]. s y Пример: 1) J x2 dx = ^ — ^ = 9-0 = 9; о 2> / rfb = * ags * C = W — (-!)) =! • -2 3) Вычислить интеграл J y 1 + c ° 9 ^ dx.♦ / 11-dx = J V cos2 xdx = J \ cos2 x \ dx = о »оо е = J cosxdx + J (-cosx) dx = Сина: ^. + (-Sina;) | ^ = 1 + 1 = 2. ♦ е 4)
Рассчитать интеграл J • е e22 ♦ [- = In I lnxll ^ = In 2-In 1 = In 2 * J X1Г1X е Людмила Фирмаль

