Оглавление:

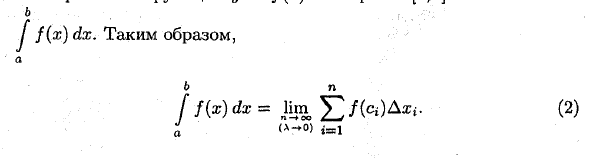


Определенный интеграл как предел интегральной суммы
- Интегралы, определенные как пределы Накопленная сумма ■ j •. , •,! ». ; ‘<■’ ■ • * • v ‘. • Предположим, что функция y = f (ar) определена в интервале [a; 6], а <6. Выполните следующие действия: 1. Используете ли вы точку х0 = а? xi, xi, …, xn-b (x0 <si <• «<n) сегмент [a, b] разделен на n частичных сегментов [a? o; ®i] i •• .. ., [Xn -i, ®n]. C \ C2 Ci Cn X -y-1 —.— I ”I — 1 — 1 — 1 — 1 — 1 — 1 — 0 a = xo xi X2 Xi b-Xn, 2. Для каждого частичного сегмента i = 1, 2, …, n выберите произвольную точку Ci € [xi-i \ xi] и вычислите значение функции в ней. То есть количество / (с *). 3. Умножьте значение найденной функции f (c, -) на соответствующую частичную длину сегмента Dx * = Xi-Xi-1: f (a) • Axi.
4. Создайте общий Sn для всех таких продуктов. N Sn = f (c1) J1 + f (c2) Ax2 + •• + f (cn) Axn = Y, (!) я = я Сумма вида (1) называется интегральной суммой функции y = f (x) в интервале [a; 6]. A = проверка A Xi (i = 1,2, …, n). 5.
Предположим, A представляет длину наибольшего частичного сегмента. Людмила Фирмаль
Когда п-ооо, найдите предел интегральной суммы (1) и установите его равным Л-0. В этом случае интегральная сумма S имеет предел I и не зависит от того, как делится интервал I [a; B], делится на частичные сегменты, а не от выбора этих точек. В этом случае число I называется определенным интегралом функции y = f (x) отрезка [a; B] и f (x) dx. Вот так / F (X) DX N B ^ 2f (0i) x (L- »o) j-!
Числа a и b называются нижним и верхним пределами интегрирования, f (x) — подынтегральное выражение, f (x) dx — подынтегральное выражение, x — переменная интегрирования, а сегмент [n] — область интегрирования (сегмент). вы. Интервал [a; B] для функции y = f (x) B ■ ‘ г Правый интеграл / f (x) dx теперь называется интегрируемым OtrVFse. но :.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Теперь сформулируем: ■ Теорема и теорема о существовании теоремы. , • [y1: теорема 1 (тренер). Когда функция y = f (x) непрерывна • ■ • & Имеется разрез [l; 6], определенный интеграл J f (x) dx. Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако для некоторых разрывных функций могут существовать определенные интегралы, особенно те, которые окружены отрезками с конечным числом разрывов.
Укажем некоторые характеристики некоторых интегралов, которые непосредственно следуют из определения (2). 1. Конкретная интеграция не зависит от спецификации переменной интеграции. б б. б J f (x) dx = f f (t) dt = J f (z) dz ..; f а Это связано с тем, что целая сумма (1) и, следовательно, ее предел (2) не зависят от того, какой символ задает аргумент этой функции. 2. Определенный интеграл с тем же пределом интегрирования равен нулю: но но 6 3.
Для любого действительного числа c: cdx = c • (b-a). но Людмила Фирмаль

