Таблица интегралов полная и формулы интегралов для студентов

Оглавление:

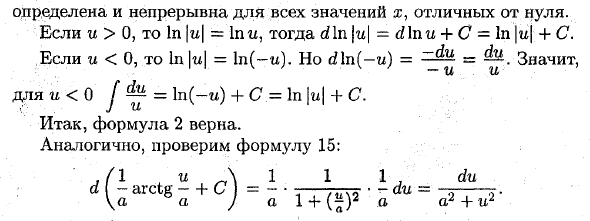
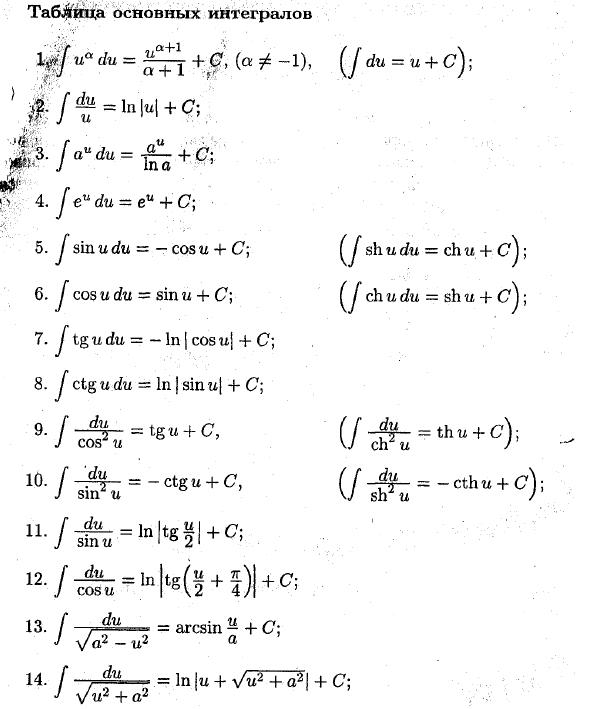
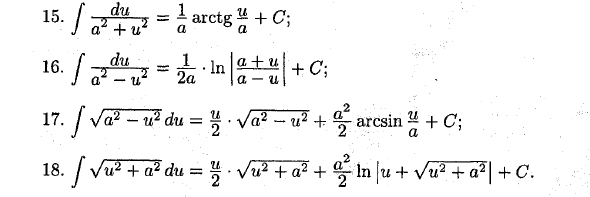
Таблица основных интегралов

Основная таблица интеграции Воспользовавшись тем фактом, что интеграл является противоположностью производной, вы можете получить таблицу базовых интегралов, перевернув соответствующую формулу производной (таблицу производных) и используя неопределенное свойство интеграла. Например, d (smu) = cos u- du} Тогда G G b / cos udu = d (sin u) = sin и 4-С. Многие табличные выражения получены при рассмотрении основных методов интеграции. , Интегралы в таблице ниже называются табличными формами. Их следует знать искренне.

Метод поиска примитивов (т. Е. Интегрирующих функций) ограничен указанием метода для интеграции этого (желательного) интеграла в одну из таблиц. Поэтому вам нужно знать интегралы таблиц и уметь их распознавать.

В интегральных вычислениях не существует простого универсального правила для нахождения примитивов из базовых функций, как в дифференциальных вычислениях. Людмила Фирмаль

Обратите внимание, что в базовой таблице интеграции интегральная переменная может представлять как независимую переменную, так и функцию независимой переменной (в зависимости от свойства инварианта интегрального выражения). Справедливость следующего уравнения можно проверить, взяв производную справа. Производная равна подынтегральной функции в левой части уравнения. Например, давайте докажем справедливость уравнения 2. функция

Решение задач по высшей математике

Действия над комплексными числами	Основные методы интегрирования
Неопределенный интеграл	Интегрирование тригонометрических функций

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Определено и непрерывно для всех ненулевых значений i. Если u> 0, In | u | = In, то dIn | u | = dIn и + C = In | u | + C В M = ln (-u), когда u <0. Но dln (-ti) = = Поэтому FOR u <0, f ~ = In (-ti) + C = In \ and \ + C Следовательно, уравнение 2 является правильным. Аналогичным образом проверьте уравнение 15. 111, ду ( (1 и d (-arctg- + C \ a и но ‘a 1 4-‘ adU a2 + i2

Основная таблица интеграции .а-я я ^ ш и ду = ч и 4-с); (^ J ч и ду = ш и 4-с ^; 1du = ff ^ -j + 0 ‘(a ^ -1), (V = + M / T-BW ^^ • J-. /;. ; » .irf & i-l u • V. $ р 4. J eu du-eu + C \ ■ 5. J sin u du = -cos u 4-C; 6. Jos u cfa = грех? I + C; 7. J tgudu = — \ n \ cosu | 4- C; 8. J ctg u du = In | sin u | 4- C; 9. [= tgti + C, J cos ^ u 10. [= -ctg u + C, J sin tl 12- / i = lnWi + l) l + C; 13. f-> du = arcsin ^ 4- C; J- и 2 a 14. [, du = In | q 4-l / q2 4-Q2! 4-C; ^

Vii2 4- a2! 5- / = ~ arctg- + C; J a ‘+ uz a * a’ 16. [1 1n a ± u + (7 J a2-u2 2a a-u ‘ 17. = | • + ^ арксин А + С; 18. |> / т? + a2dti = | • h / u2 + a2 + ^ In | u + vV2 + a2 | + C Людмила Фирмаль