Оглавление:







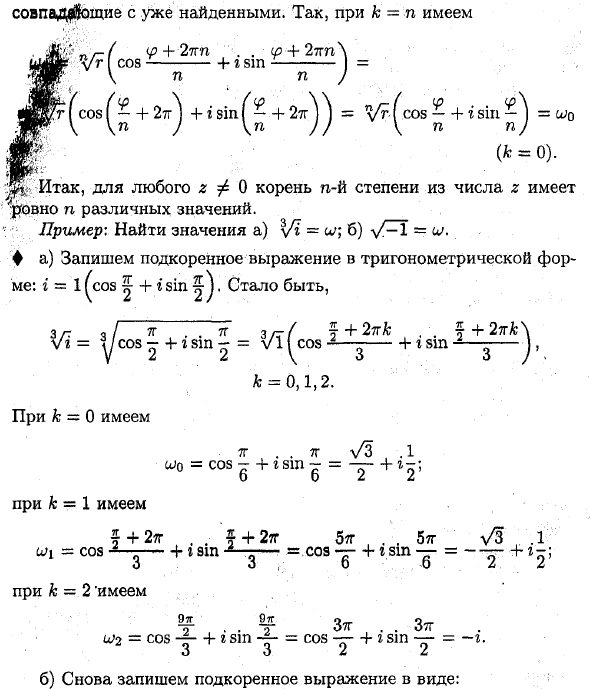
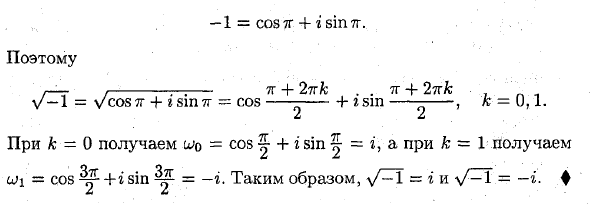
Действия над комплексными числами
- Действие на комплексные числа (1) ZI + Z2 «G- -Z \ О ~ X Включение комплексных чисел обладает прерывистыми (коммутативными) и комбинированными (ассоциативными) свойствами. 21 + 22 = Z2 + 21 (21 + Z2) + 23 = 21 4- (z2 + 2x). Из определения (1) геометрически комплексные числа добавляются как векторы. Вы можете видеть прямо из рисунка \ zi + z2 \ ^ \ z \ \ + \ z2 .
1. Добавление комплексных чисел На бумаге с двумя комплексными числами z ±. = X \ + iyi и z2 = x2 + iy2, существуют комплексные числа, определяемые уравнением Zi + Z2 = (xi + x2) 4-i (yi + J / 2). -1 = cos 7G 4-g sin 7g так ■ —- 7 г + 27 г , 7g -f 2ttk. ». V -1 = VCOS7T -f 2Sin7T = cos — + gsin —, k = 0,1. z z Если k = 0, u> o = cos ~ + i sin ^ = r получается, и если k = 1, получаются wi = cos- и sin ^ = -r. Следовательно, y / <Λ = r и> / -! = -g. ♦
Это соотношение называется неравенством треугольника. Людмила Фирмаль
Вычитание комплексного числа -C- ‘ Вычитание определяется как противоположность сложению. Разница между двумя комплексными числами Z1 и z <i ‘является таким комплексным числом r, и при добавлении к m, если t-Z2 = Z1, то от z до z \ -z-2 Если zi = x \ + iyit Z2 = x2 + ij / 2, вы можете легко получить из этого определения ».I.. в z2 V хорошо О Х z-Z \ -z-2 ~ (xi-x2) + r (y i-y2) (2) Из уравнения (2) геометрически Комплексные числа вычитаются как векторы. Вы можете видеть прямо из рисунка \ zi-z2 \ ^ | zi | — \ z2 . Обратите внимание, что \ z \ -Z21 = y / (x \ -Z2) 2 4- (2/1-y2) 2 = d, То есть модуль разности между двумя комплексными числами равен расстоянию d между точками, представляющими эти числа на плоскости.
Таким образом, например, уравнение: -2g | = 1 определяет множество точек z на расстоянии 1 от точки * o на комплексной плоскости. То есть окружность с центром в zo = 2r и радиусе 1. <» ^ «* с. ^ Сложное умножение » Произведение комплексных чисел Zi ~ x \ + iyi и z-i-xi + iy-2 является комплексным числом, определяемым уравнением z = ZiZ2 = (arxlr-2 / 12/2) + r (xx2 / 2 + yx ^ z) (3) «Отсюда, особенно самые важные отношения V— • ■ • — (4) r2 = -1
| Формула Тейлора | Неопределенный интеграл |
| Понятие комплексного числа | Таблица основных интегралов |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Фактически, i2 = U = (0 + 1g) (0 + 1g) = (0-1) + g (0 + 0) = -1 (4), так что уравнение (3) является биномиальным xy + iyi и i ? + gu2 ‘ (^ 1 + + iy2) = ^ 2 + + + UftLUte = = XyX2 4-r2y \ y2 + + = -2 / W + i (si2 / 2 + Y \ x2) Например (2-3 г) (-5 + 4 г) = -10 + 8 т + 15 г-12 г 2 = -10 + 23 г 4-12 = 2 + 23 г Обратите внимание, что согласно уравнению (3) zz = (x + ft /) (ar-iy) = x2 + y’2. Комплексное умножение обладает свойствами нераспространения, объединения и распределения (распределения). Z1Z2 = Z2Z1 , (21 * 2) 23 = джипаджи), Z \ (z2 + Zz) -Z1Z2 + Z \ ZzЭто легко проверить с помощью определения (3). Произведение комплексного числа z1 = ri (cos 2 + cosi /? I sin
Это значит « = rir2 (cos (v? i 4-y> 2) 4-i sm (v? i 4- (p2)). Они сказали, что умножение комплексного числа обернет модуль ножом и добавит аргумент. Это правило применяется к любому конечному числу , В частности, если есть n факторов, и они все одинаковы, , , ‘fa zn = (g (cos 4-i sin ip)) n = 7- «(cos nip -hi sin nip) (5) RP- Уравнение (5) называется уравнением муара. Пример: Найти (1 4- \ / 5g ‘) 9. ♦ Сначала запишите числовое значение z = 14-l / 3g в тригонометрической форме. , — r = y 1 -f (h / w) 2 = 2; argz = arctg- IT ✓ L-. , 7G \ ==> argz = z = 2. ^ cos-4-g sin-J По формуле Мура z9 = (1 4-VZi) 9 = 29 (cos9 до 4-i sin9 J) = = 29 (cos3tt 4-isin37g) = 2b (-1) = -512. ♦ 4. Комплексное деление
Частное двух комплексных чисел Z1 и z2Φ0 является комплексным числом r, и при умножении на z2 получается число Z1. Zs if ^ -z2z = z . -z2 z \ -xi + iyi, z2-x2 + iy2Φ0, 2 = x + iy, уравнение (x2 + iy2) (x + iy) = xi -J-iyi \ xx2-yy2 ~ xu \ xy2 + yx2 = y i. : Решение системы находит ценность хны. \ ~ Ж1Ж2 + 2/12/2 _ Y 1 ^ 2- -f y | ‘Y к x% + y1
Деление определяется как противоположность умножения Людмила Фирмаль
Следовательно, * = & = ^^ + Ur + ~ x} p, + ^ + 2/2 Фактически, отношение двух комплексных чисел Умножьте числитель и знаменатель на сопряженное число знаменателя («Уберите мнимое число знаменателя»).
Пример: выполнение деления Z «T 1 1 + 2C1 + 3i) (2-i) 2-g-f 6g + 3 = 5 + 5g +. * 2 + т. ~ (2 + «) (2-р) ~~ 4 + 1 5 ~ + f Для сложных тригонометрических форм формат выражения деления: t * 1 (cos (fi + i sin (pi) 7 * i // . •• / n ——-—— = — (C0S ( 11- n = z, то Ч / z = u. Размещение z r (cos = p (cos 9 + r sin sin #), благодаря определению маршрута и формуле муара, от z до iun s; (cos nO + g sin nv) = r (cos n / p (арифметический корень).
Таким образом, уравнение fy / z = принимает вид: Vr (coscp + isincp) = Y? (Cos ^ + — ^ j i 8sh ^ ‘| e \ n n) fc == 0,1 ,: .., n-1 Получите n разных значений маршрута. A: Для других значений корневое значение получается по периодичности косинуса и синуса.Уже найдено. Поэтому для к-м W -p.r- (Ch> + 2rn .. (P + 2rrn \ p Vr cos —4- r sin- = / V р р) Wx (C0S (£ + 2ff) + ‘^ (n +) = ^’ (co n + * sin d) = a; ° (* = 0). G. Следовательно, для любого 2 ^ 0 корень m-го порядка z имеет разные значения jtobhoη. Пример: а) Найти значение V * = и /; b) = o /. ♦ a) Запишите выражение радикала в виде треугольника: i = 1 ^ cos j + r sin ^. так sG s / * -s / — / f + 2tL :. f + 2tgAL h / g = y cos- + g sin- = VII cos-—— + g sin-—— J, А = 0,1,2. Если k = 0, Tg. , tm / 3 .1 c ^ o = cos- + tsm — = — + r-; Когда k = 1 F + 2TG. , $ + 2тг 5тг , 5tr \ / 3 .1 w \ = cos- + r sin- = cos- + tsin— = -; Когда k = 2 т. T Ztg. , Htt u; 2 = cos + g sin = cos- + g sin- = -g О О * З б) снова напишите выражение маршрута в следующем формате:

