Формула Тейлора и определение функции

Оглавление:

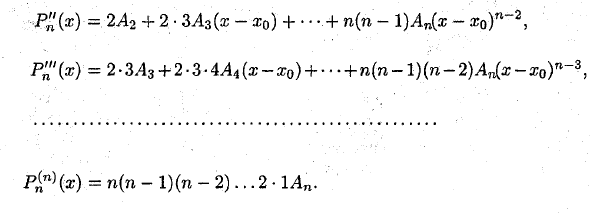
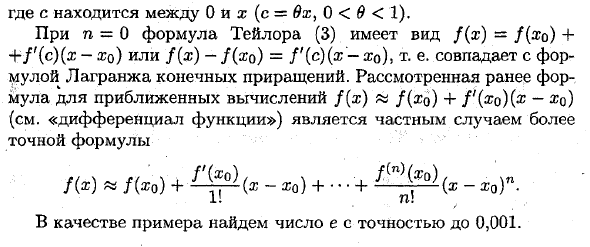
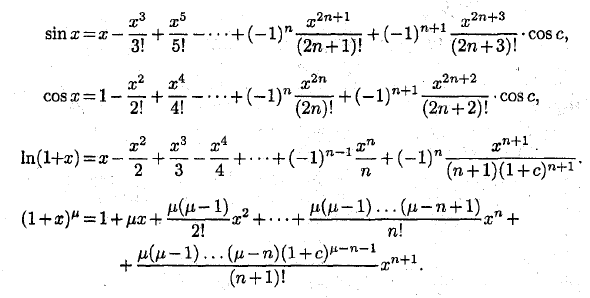
Формула Тейлора

Формула тейлора Определение функции y = f (x) не означает, что значение y можно найти по значению x. Из них t3 Если функция является выражением вида y = ^ -bx + 7 Значение функции можно легко найти с помощью четырех арифметических операций. Но как найти значение функции y = sin x, y = in (l + x) для любого (допустимого) значения аргумента, например? Чтобы вычислить значение данной функции y = f (x), ее заменяют полиномом Pn (x) степени n, и ее значение всегда легко вычисляется.

1. Полиномиальная формула Тейлора Предположим, что функция f (x) является полиномом Pn (x) степени n: f (x) = Pn (x) = ao 4-a \ x + a2x2 + .. + apxn. Этот многочлен также преобразуется в многочлен степени n относительно разности x-xq. Где xq — произвольное число То есть Pn (x) представляется в следующем формате: Pn (®) — ‘= Ao + Ai (x-x0) + A2 (x-x0) 2 + •• + An (x-z0) n. (1) Чтобы найти коэффициенты Ao, Ai, …, An, дифференцируем уравнение (1) n раз. P’n (x) = Au + 2A2 (x-x0) + 3A3 (x-x0) 2 + ••• + 7An (x-®0) n ~ \ RC (x) = 2Ao + 2 • 3L3 (x-l0) H- • + n (n-1) An (x-x0) n ~ 2, RC ‘(x) = 2-3A3 + 2’3-4Ai (От X до xo) + — + n (nl) (n-2) Av {x-xo) n- \ P (n) (x) = n (n-1) (n-2) … 2 • 1A

Обоснование возможности выражения функции в виде полинома дается формулой Тейлора. Людмила Фирмаль

Подставляя x = x0 в полученное уравнение и уравнение (1), PnM = L0, то есть Aq = Pn (xo.) J KY = Ai или L = Pn (x0) -2dr, то есть = Pn (xo) -2 • ЗАЗ, т.е. = pM (x0) = n (n-1) .. .2 ■ Ln, то есть A „=» 77! Подставим найденные значения Ao, Ai, …, An в уравнение (1), чтобы получить полиномиальное разложение порядка n в Pn (x) как степень (x-xo). Pn (x) = Pn (xo) H! C ^ (x-xo) + -ao) 2+ … + {x „Jo) n. (2) P! Уравнение (2) называется уравнением Тейлора порядка n полинома Pn (a;).

Пример: Раскройте полином P (x) = -4a; 3 4- Over: в степенях 2-2x + 1 x x. ♦ где a; o = -1, P ‘(x) = -12×2 + 6z-2, P «{x) = -24x + b, P'» {x) = -24. Следовательно, P (-1) = 10, P ‘(-1) = -20, P «(~ 1) = 30, P»‘ (-1) = -24. так P (W) = ω + = ™ (x + 1) + + 1) 2 + = ™ (x + 1) 3 Это -4s3 + Zx2-2x + 1 = 10-20 (® + 1) + Schx-I) 2-4 (w 4-1) 3. ♦ 2. Функция Тейлора любой функции Рассмотрим функцию y = f (x). Формула Тейлора позволяет аппроксимировать функцию f (x) в виде полинома при определенных условиях и дать оценку погрешности этого приближения.

Решение задач по высшей математике

Асимптоты графика функции	Понятие комплексного числа
Общая схема исследования функции и построения графика	Действия над комплексными числами

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Теорема 1. Если функция f (x) определена в окрестности xo и содержит производные до (n 4-1) порядка, то x из этой окрестности имеет точку 6 (xo; x) Да, выражение верно / () = / ( O) + -xo) + ^ (x-xo) 2 + … , / ()) (^ O) гр м ^ н. / (P + 1) (s) Gt : — + (X’X0) + 1 . Здесь, • Pn (®) = f (oo) + ^ (X- * o) + — * 0) 2 + … п! Ай называется полиномом Тейлора? n (a?) = ^ ~ £ o) n + 1 Называется остаток формулы Тейлора, написанный в формате Лагранжа. Rn (x) — ошибка приближенного уравнения f (x) ≥Pn (x).

Если ggo = 0, вы получите специальный случай формулы Тейлора и формулы Маклаурина.с составляет от 0 до х (с = 9х, 0 <9 <1). Если n = 0, формула Тейлора (3) имеет вид x-a; Ранее рассмотренная формула для приближенного вычисления f (x) и f (xo) -f f ‘(xo) {x-xq) (см. Раздел «Разграничение функций») является частным случаем более точной формулы. Fix) // (x0) + -x0) H —- + -x0) n. В качестве примера найдите число e с точностью до 0,001.

Таким образом, уравнение Тейлора позволяет заменить функцию y = f (x) полиномом y = Pn (x), что дает разумную точность, равную значению остаточного члена Hn (x). Людмила Фирмаль

Напишите выражение Макларанаделла с функцией f (x) = ex. Найдите производную этой функции: f ‘(x) = ex, f «(x) = ex, …, f (n + 1 ^ (x) = ex. F (0) = e ° = 1 , / ‘(0) = e ° = 1, …, f <*> (0) = 1, f (n + 1> (c) = ec и согласно уравнению (4): х х2 х3 х экррн + 1 er = 14-yy + -yy + -yy + 1! 2! 3! п! (N + 1) G положить х = 1 111 ‘1 ес е = 1 + + ^ + + 1! : 2! 3! п! (N + 1)! ‘ Чтобы найти e с точностью до 0,001, определите n из условия, что остаточный член ^ <j меньше 0,001. Поскольку 0 <c <1, ес <3. Так что, если n = 6, ^ <= 0,0006 <0,001. Получите приближенное уравнение i, 1 111 1 ■ e «1 + 1 + 2! + 3! + 4! + 5! + b!% « 2 + 0,5 + 0,1667 + 0,0417 + 0,0083 + 0,0014 = 2,7181 » 2,718, Другими словами, е »2.718. …. ♦ Ниже приведено расширение выражения Маклорина для некоторых других основных функций.–5 * T2n + 3 • я X2 X4 x2n x2n + 2 т. 2 ^ n 1 2! п! + (N + 1)! Z ‘