Оглавление:



Общая схема исследования функции и построения графика
- Общая схема функционального исследования и графического построения Рекомендуется, чтобы исследования функции y =} {x) проводились в определенном порядке. 1. Найдите область действия функции. 2. Найти пересечение графика и координатных осей (если это возможно). 3. Найдите постоянное расстояние между символами функции (f (x)> 0 или f (x) <0). 4. Проверьте, является ли функция четной, нечетной или общей. 5. Найдите асимптоту графа функции. 6. Найти интервал монотонности функции. 7. Найти экстремальное значение функции. 8. Найдите выпуклые интервалы и точки перегиба в графе функций.
Создайте график функции на основе ваших исследований. В простых случаях достаточно выполнить всего несколько операций, например 1, 2, 7 и т. Д. Если график функции не совсем понятен после выполнения всех восьми операций, вы можете дополнительно изучить периодичность функции, создать некоторые дополнительные точки на графике и определить другие функции функции. , Может быть желательно построить график функций с течением времени для проведения исследований. Пример: проверьте и нанесите на график функцию f = x%. 1- «» C
Вышеуказанная схема опроса не является обязательной. Людмила Фирмаль
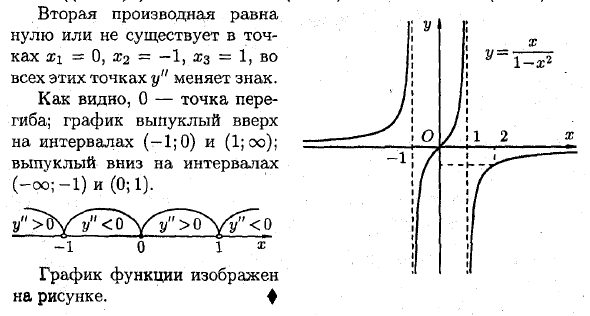
♦ Выполните все восемь операций схемы исследования, предложенной выше. ; 1. Функция не определена для x = 1 и x = -1. Область определения состоит из трех интервалов (-os; -1), (-1; 1), (1; + oo) и трех графиков ветвей. 2. Если х равен 0, у = 0. График пересекает ось Oy в точке 0 (0; 0). Если y = 0, x = 0. График пересекает ось Ox в точке 0 (0; 0). 3. Функция положительна (y> 0) в интервале (-oo; -1) и (0; 1). Отрицательные признаки — (- 1; 0) и (1; + оо). 4.
Поскольку y (-x) =, функция y = x -2 нечетна. 1-х = — ~ X = -x ^ = —Y В результате график Метрика о происхождении. Чтобы построить график, достаточно взглянуть на x ^ 0. 5. Линии I = 1 и I = -1 — их вертикальные асимптоты. Проверьте наличие диагональных асимптот: ….. я k = lim = lim- ^ = 0, X-400 x X- + OS 1-X (X => -nos и a: k = 0 как -oo), B = lim (X-Ox) = lim x = 0 w —►oo1-x x- »oo 1-x В результате возникает горизонтальная асимптота, и каково ее уравнение? / = 0. Прямая y = 0 является асимптотой x + oo и x-> -o. 6. Найдите интервал между функцией увеличения и функцией уменьшения. с того времени , = / Xy_1 (1-x2) -x (-2x) _x2 + 1? Y ~ V1 ~ a2 / (1-X2) ‘2 «» (1-x2) 2’
| Выпуклость графика функции, точки перегиба | Формула Тейлора |
| Асимптоты графика функции | Понятие комплексного числа |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Тогда 2 / ‘> 0 в области определения, и функция увеличивается в каждом интервале области определения. Т. Изучите функцию экстремального значения. Так как у ‘= ^, (1-г) Критическими точками являются точки xi = 1 и X2 = -1 (y не существует), но они не принадлежат области определения функции. Здесь нет функции экстремального значения. 8. Изучите выпуклую функцию. «: (1-x2) 2; (1-x2) 4 (1-x2) * •
Вторая производная равна нулю или не существует в точках X1 = 0, X2 = -1, X3 = 1, все эти точки y меняют знак. Как видите, 0 — это точка перегиба. График выпуклый вверх с интервалами (-1; 0) и (1; °). Выпуклый вниз через равные промежутки времени
Нарисованный график функции (-Oo; -1) и (0; 1). ♦ На рисунке. Людмила Фирмаль

