Оглавление:

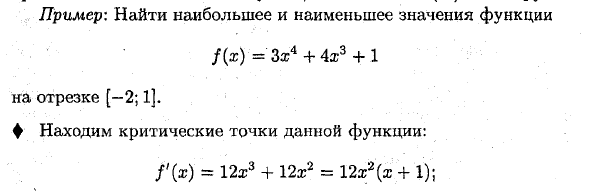


Наибольшее и наименьшее значения функции на отрезке
- Максимальные и минимальные значения функции резки Функция y = f (x) является интервалом [a; B]. Как известно, такая функция достигает максимальных и минимальных значений. Функция может принимать эти значения во внутренней точке Xq сегмента [a; b] или на границе сегмента, т.е. x0 = a * или xo = b. Для x0Å (a; 6) найдите точку x0 среди важных точек этой функции.
. 1) Найти критическую точку функции в интервале (a; b). 2) Рассчитать значение функции в найденной критической точке. 3) Рассчитать значение функции на обоих концах сегмента, т.е. в точках x = a и x = b 4) Выберите наиболее среди всех рассчитанных значений функции Шея и самая маленькая.
Получить следующее правило, чтобы найти максимальные и минимальные значения функции [a; d] Людмила Фирмаль
Примечания: 1. Функция V = f (x) имеет только одну критическую точку в интервале [a; 6], которая является максимальной (минимальной) точкой, в которой функция принимает максимальное (минимальное) значение , На рисунке / (®®) = / „6 = / max- (nb — максимум, максимум — максимум). 2. Если функция y = f (x) сегмента (a; 6) не имеет критической точки, это означает, что функция монотонно увеличивается или уменьшается, поэтому функция является максимальной на одном конце сегмента Значение (М) минимальное (га) выше другого. в о х но эй Пример: Найти максимальные и минимальные знаки / (X) = 3z4 + 4z3 + 1 Сегмент [-2; 1]. ♦ Найти критическую точку этой функции: (Х) = 12z3 + 12a: 2 = 12x \ x + 1);
f ‘(x) -0. Xi = 0 € [-2; IJ и x-2 = -1 € • [–2; 1]. / (0) = 1, / (-1) = 3-4 + 1 = 0, / (-2) = 48-32 + 1 = 17 / (1) = 8. Следовательно, / „b = точка x = -2 в 17, точка g = -1 при нм = 0 ♦ Нахождение максимальных и минимальных значений функции широко используется для решения многих практических задач в математике, физике, химии, экономике и других областях.
| Возрастание и убывание функций | Выпуклость графика функции, точки перегиба |
| Максимум и минимум функций | Асимптоты графика функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Практические задачи: задачи по транспортировке товаров с минимальными затратами, задачи по организации производственных процессов для максимизации прибыли и другие задачи, связанные с поиском наилучшего решения, максимального и минимального Это приводит к разработке и совершенствованию метода поиска ценностей. Линейное программирование, специальный отдел математики, занимается решением таких задач. Рассмотрим более простую задачу.
Вырежьте самый большой объем цилиндра из шара радиуса R. Какой размер? ♦ Используйте хну, чтобы указать высоту и диаметр цилиндра. Далее, как видно из рисунка, у = \ / 4 # 2-π2, поэтому объем цилиндра .. …. / 4R2 x2 \ ‘_2 V-V (x) = 7Γ (— J X = 7rH x-J-, Где x e [0; 2R}. Найти максимальное значение функции V = V (x) в интервале [0; 2H]. Поскольку V ‘(x) = η # 2- | η: 2, a: = Далее, V’ (x) = 0, поэтому V «(®) = -1r <0. Следовательно, л / з — максимум Поскольку функция имеет одну критическую точку, цилиндр х = максимальный объем по диаметру (равен Vmax) Цилиндрические днища равны о
Следовательно, целевой цилиндр имеет высоту, равную f, и диаметр, равный f. Людмила Фирмаль

