Оглавление:

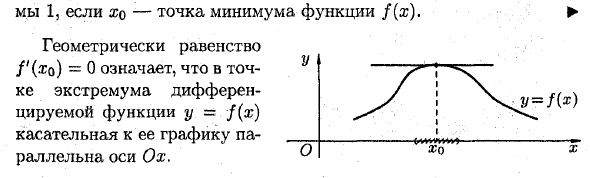



Максимум и минимум функций
- Максимальные и минимальные функции Точка x0 называется точкой максимума функции y = f (x), если существует окрестность xq, где f (x)>} (xo) для всех xΦxq из этой окрестности. Минимальная точка функции определяется аналогичным образом: xq — минимальная точка функции для 3 <5> 0 Yx: 0 <\ x-x0 \
we 1, если xo — минимальная точка функции f (x). ► Геометрически уравнение f ‘(xo) = 0 означает крайнюю точку дифференцируемой функции y =} (x), а касательная графика параллельна оси Ox. То есть, если e ^ и f ‘(x0) = 0, это не значит, что xq — крайняя точка. Например, для функций y = x3 Его производная y ‘= 3×2 равна нулю при x = 0, но x = 0 не является крайней точкой. Некоторые функции не имеют производных в крайних точках. Например, непрерывная функция y =). R * | В точке x-0 нет дифференцирования, но точка x-0 является минимальной точкой.
Обратите внимание, что обратная теорема неверна. Людмила Фирмаль
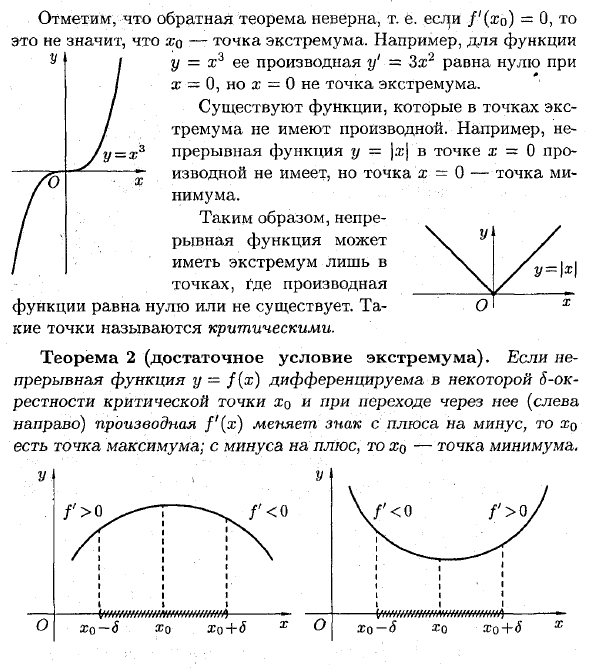
Таким образом, непрерывная функция может иметь экстремальные значения только в точках, где производная функции равна нулю или не существует. Такие точки называются критическими. Теорема 2 (полное условие для экстремальных значений). Когда непрерывная функция yf (x) дифференцируема вблизи S с критической точкой Xo и проходит через нее (слева направо), производная f ‘(x) меняет знак с плюса на минус, а xq Максимальная точка, от отрицательной до положительной, xq — минимальная точка. 1 час г х \ U / Y = \ x «О Х В |! Хо-6 Хо +6 f> 0 Хд -tyM / tWWfffHHWMtWMft, ■ tytH / MtHHHMwmMfHHA- о X XO-s Хо + д о
(5 окрестностей точки m0, предположим, что условие выполнено: f ‘(x)> 0 Vx6 (x0-8 \ x0) и}’ (x) <0 Vt € (m0; m0 + 6 Затем функция} {x) увеличивается с интервалом (then-6 \ xo) и уменьшается с интервалом (.to; x * o + <5). Значение точки xG} (x) является максимальным в интервале (x0- <5; x0 + <$}, т.е. f (x) 0 Vt € (x0; m0 + <$) • ►Изучение функции экстремумов означает поиск всех ее экстремумов.
| Раскрытие неопределенностей различных видов | Наибольшее и наименьшее значения функции на отрезке |
| Возрастание и убывание функций | Выпуклость графика функции, точки перегиба |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Теоремы 1 и 2 означают следующие правила для исследования экстремальных функций: 1) Найти критическую точку функции y = f (t). • 2) Выберите только те, которые являются внутренними точками домена определения функции. .. 3) Изучите знак левой / правой производной / ‘(.t) каждой выбранной критической точки. 4) Запишите экстремальные точки (если таковые имеются) в соответствии с теоремой 2 (достаточное условие экстремумов) и вычислите значения этих функций. * Пример: Найти экстремальное значение функции y = — 12 1 3 / д ♦ Очевидно, D (y) = K. Вы можете найти y ‘= ^ — ^, то есть y’ = — •. + — +
Производная не существует при x \ = 0 и не равна нулю при X2 = 8. Эти точки делят всю область этой функции на три интервала (~ oo; 0), (0; 8) и (8; oo). На рисунке показаны знаки левой и правой производных каждой критической точки. Основываясь на вычислении знака второй производной, может быть удобно использовать другой достаточный признак существования экстремальных значений.
Следовательно, xi = 0 — максимальная точка, duck = y (0) = 0, x-2 = 8 — минимальная точка, ut = y (8) = ♦ Людмила Фирмаль
Теорема 3. Если первая производная функции f (x) равна нулю (f ‘(xo) = 0) в точке x0, а вторая производная существует в точке xo и не равна нулю (f «(xo) Φ0) при f «(xo) <0, то функция в xo имеет максимальное и минимальное значения -f» (xo)> 0.»4 для детерминизма» {xo)> 0. f «(xo) = lim H * o + A ) — / ‘( o) = lim fe ± M> 0, f’ (xo + Lx)> 0 J-> 0 Dx- * 0 / LA Для достаточно малой окрестности Ax <0 в точке n0 f ′ (x0 + Az) <0, для Ax> 0 f ′ (x0 + Ax)> 0. Таким образом, при прохождении через точку x0 первая производная меняет знак с отрицательного на положительный. Следовательно, в теореме 2 xq является минимальной точкой. Аналогично, если} «{x0) <0, функция оказывается максимальной в точке x. ►

