Оглавление:
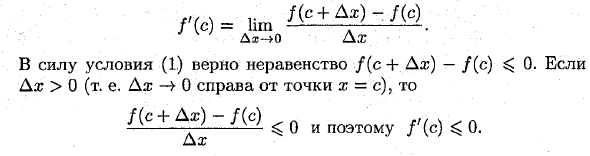
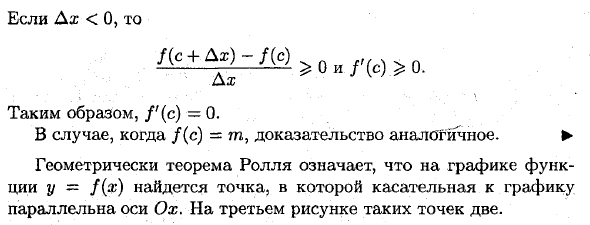
Теорема Ролля
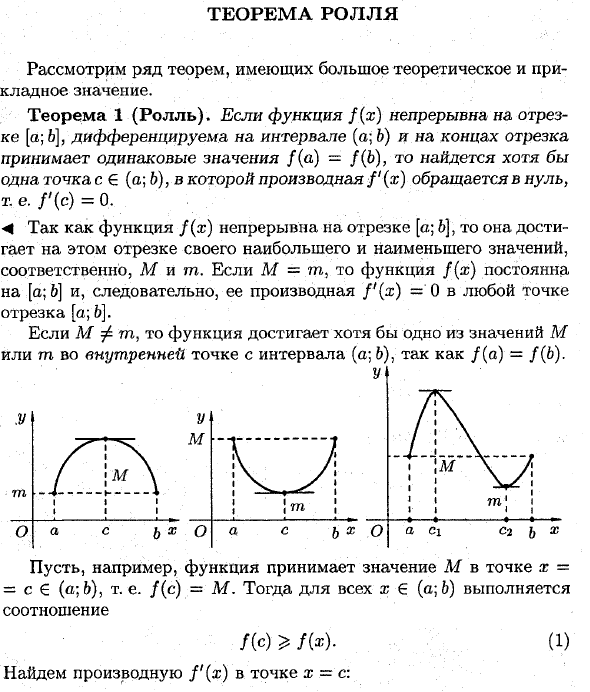
- Ролевая теорема Рассмотрим ряд теорем больших теоретических и прикладных значений. Теорема 1 (катушка). Если функция f (x) непрерывна в интервале (a; 6), дифференцируема в интервале (a; b) и принимает то же значение f (a) = f (b) в конце интервала, по крайней мере, один Точка c € (a; B), производная f ‘(x) исчезает, т.е. f’ (c) = 0 ■ 4 функции / (x) достигают интервала [a; 6], затем достигают максимального и минимального значений в этом сегменте, Миш, соответственно.
Если = = m, функция f (x) является константой с [a;. 6], следовательно, производная f ′ (x) = 0 B] в любой точке интервала [a; В случае MΦmn, поскольку f (a) = f (b), функция достигает хотя бы одного из значений M или mn во внутренней точке из интервала (a; 6). .
Y TP g Y ^ sT M M \ -KU Y 1. 1 1 • 1 | т т \ О б х о б б о б а у б х о Людмила Фирмаль
| Применение дифференциала к приближенным вычислениям | Теорема Коши |
| Дифференциалы высших порядков | Теорема Лагранжа и ее следствия |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Например, предположим, что функция принимает значение M в точке x = c € (a; &), то есть f (c) = M. Тогда все x € (a; b) соотношения f (c) e f (x). (1) Найти производную f ‘(x) в точке x = c.
Ps) = lim Дх> о да. Согласно условию (1), неравенство f (c + Ax) — / (c) <0. Если Ax> 0 (то есть Ax 0 = c справа от точки a) f (c + Ax) -f (c) ^ 0 Поэтому ^ 0 о Если Dx <0, / (S + Dx) — / (s) Dx ^ 0 и / ‘(c) ^ 0. Следовательно, f ‘(c) = 0. Если f (c) = m, доказательство аналогично. ► Геометрически теорема Ролла означает, что на графике функции y = / (x) есть точка, в которой касательная графика параллельна оси Ox.
Третья фигура имеет две такие точки. Людмила Фирмаль

