Оглавление:


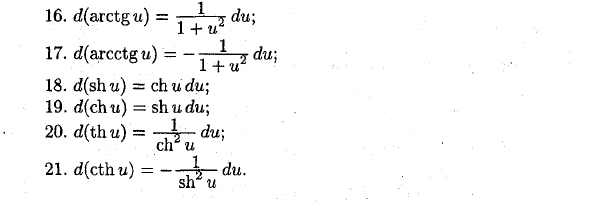
Основные теоремы о дифференциалах. Таблица дифференциалов
- Основная теорема о дифференцировании. Дифференциальная таблица Теорема об основной производной может быть легко получена с использованием соотношения между производной и производной функции (dy = f ‘(x) dx) и соответствующей теоремы о производной. Например, производная функции y = c равна нулю, поэтому производная от постоянного значения равна нулю. dy = с ‘dx = = 0 • dx = 0.
Теорема 1. — Например, давайте докажем второе выражение. В зависимости от определения дифференциации существуют: d (uv) = (tiu) ‘cte = (u’u + uv’) dx = r> • u’dx + u • v’dx = vdu + udv. ► Теорема 2. Производная комплексной функции равна произведению производной этой функции по промежуточному аргументу и производной этого промежуточного аргумента. •
Сумма, произведение и частная производная двух дифференцируемых функций определяются d (u + v) = du + dv, d (uv) = v-du + u-dvi ru \ vdu-udo. y lch dU) = -. (^ O) Людмила Фирмаль
Пусть y = f (u) и u = <p (x) две дифференцируемые функции, образующие комплексную функцию y = f (tp (x)). По производной комплексной функции y’h = y’i-K- Умножение dx с обеих сторон этого уравнения дает y’xdx = = у’и • ulx dx. Где yx dx = dy и ux dx = du. Таким образом, последнее уравнение можно переписать как dy = y’i du. ► Сравнивая выражения dy = y’x • dx и dy = y’y • du, первая производная функции y = f (x) не зависит от того, является ли аргумент независимой переменной или другой функцией Определяется по той же формуле. Довод.
| Производные высших порядков | Применение дифференциала к приближенным вычислениям |
| Дифференциал функции и его геометрический смысл | Дифференциалы высших порядков |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Это свойство дифференциации называется инвариантностью (инвариантностью) в виде первой производной. Появление выражения dy = y’x • dx} соответствует выражению «ty-Yi», но между ними есть принципиальные различия. В первом выражении x является независимой переменной, поэтому dx = Дя, во втором выражении есть функция x, так сказать, в общем, du f A и. Используя определение дифференцирования и основную теорему дифференцирования, вы можете легко преобразовать таблицу дифференцирования в таблицу дифференцирования.
Например, d (costi) = (cos u) ‘n • du = -sinu • du. Дифференцирующий стол 1.d (u ± v) = du ± dv; 2. d (u -v) = vdu + и dv, особенно d (cu) = с • du; 3.rf (M) = особенно vdu-udvt = 4. Если y = f (x), dy = y’x dx. Если 5-dy = y’u-du, r / = f (u), w = <p (x) \ 6.dc = 0; 7. d (ua) rra -u0’1 • du; 8. d (aw) = au • a • du, особенно d. (Ес) = ес • рфу; 9. d (logn u) = t-d • du, особенно d (log u) = ~ • du \ 10.d (sinw) = cos udu \ 11.d (cosii) = -sin udu \ 12. ditgu) = — \ r-du; cos’2 w 13. e / (ctgu) = -rL — du; С грехом 14.d (arcsinu) = — ^ du: 15. d (arccosu) = -y ^ du; ил-u2 d (axctgu) =} 2 du;
День 1 17. dfarcctg u) = -i} l du; 1 Fu 18. рф (шу) = чу’рфу; 19. рф (чу) = шурфу; 20. д (чт) = -X-ду \ 4 ‘dT u 21. d (cthu) = -L — du. дерьмо Людмила Фирмаль

