Оглавление:



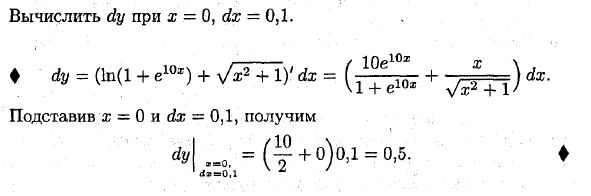
Дифференциал функции и его геометрический смысл
- Разные функции и их геометрические ощущения Предположим, что функция y = f (x) имеет ненулевую производную lim-f ‘(x) Φ0 в точке x. Далее, по теореме о связи между функцией, ее пределом и минимальной функцией, =} ‘(X) a, где o: -> 0 да; 0 или Ay = f’ (x) • Ax -f a • Ax. Таким образом, приращение функции Ay является суммой двух слагаемых f ‘(x) • Ax и a • Ax и бесконечно, если Да: -> ■ 0. Кроме того, первый член бесконечно мал. f ‘(x) -Ax lim ^ — = f ‘(x)> 0, поэтому ограниченная функция того же порядка, что и Ax
Поэтому первое слагаемое f ‘(x) • Ax называется основной частью приращения функции Ay. Производная функции y = f (x) в точке x является основной частью ее приращения, которая равна произведению производной функции и приращения аргумента и обозначается через dy (или df (x)). dy = f ‘(x) • Ax. (1) Производная dy также называется первой производной. Найти производную независимой переменной x, то есть производную функции y = x. Поскольку y ‘= x’ = 1, согласно уравнению (1), dy = dx = Дя. То есть производная независимой переменной равна приращению этой переменной dx = Ax.
Второе слагаемое является бесконечно малой функцией выше, чем Ax. т. Ох .. lim- = lim ac = 0. Дх-я) ах дх-> 0 Людмила Фирмаль
Таким образом, уравнение (1) можно записать в виде dy = f (x) dx, (2) Другими словами, производная функции равна произведению производной этой функции и производной независимой переменной. Уравнение (2) означает уравнение ^ = исправить). Здесь обозначение производной ^ можно рассматривать как отношение дифференциала dy и dx.
| Логарифмическое дифференцирование | Основные теоремы о дифференциалах. Таблица дифференциалов |
| Производные высших порядков | Применение дифференциала к приближенным вычислениям |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Найти геометрическое значение дифференциации. Y 1 / Y = Hx) / Y + A? / Ay Y Ml / м »1 Ax ‘1 A i Х х + топор х Для этого нарисуйте MT-касательную к графику функции y-f (x) в точке M (x; y) и рассмотрите ординату этой касательной в точке x + Ax. На рисунке AM = Ax, AM \ = Au. Из правого треугольника МАБ: AB tga = -То есть AB = tan a • Lx. о Но в соответствии с геометрическим значением производной tan a = f ‘(x). Следовательно, AB = f ‘(x) • Ax.
Сравнение результата с уравнением (1) дает dy = AB. То есть производная функции y = f (x) в точке x равна приращению касательной ординаты к графику функции в этой точке, когда x получает приращение Ax. Это геометрическое значение дифференциации. Пример: 1. Найти производную функции } {x) = 3z2 -sin (l + 2ar); ♦ по выражению dy = f ‘(x) dx dy = (больше; 2-sin (l + 2x)) ‘dx = (6x-2cos (l + 2x)) dx. ♦ 2. Найти дифференциальную функцию dy = ln (l + e10x) + \ Lc2 + 1. Рассчитайте dy с x = 0 и dx = 0.1. ♦ dy = (ln (l + eWl) + у / * П) ‘dx = + vjfrt) ^
Подстановка x = 0 и dx = 0.1 дает: H = 0, = (y + o) od = 0,5 1 д, = о.и 4 з 7 Людмила Фирмаль

