Оглавление:

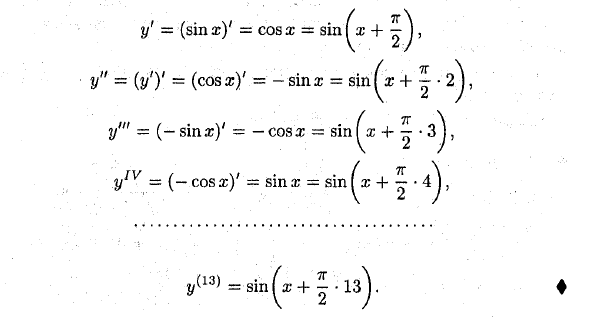

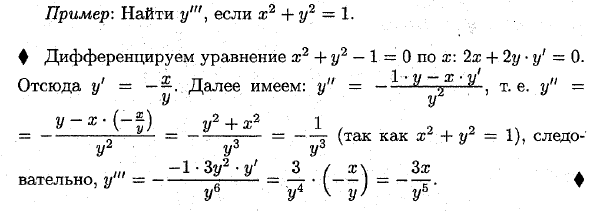

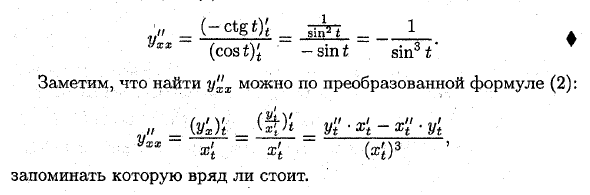
Производные высших порядков
- Высшие производные 1. Высшие производные явно определенных функций Производная y ‘= f’ (x) функции y = f (x) также является функцией от x и называется первой производной. Если функция f ‘(x) дифференцируема, ее производная называется второй производной и обозначается как «(или f» (x). & ■ £ (£) ■ — «у.
‘. N-ая производная (или n-ая производная) является производной (n-1) -ой производной. у ^ = Следующая производная на первой называется производной высшего порядка. Начиная с 4-й производной, производная обозначается римской цифрой или числом в скобках (yv или 5-я производная) Пример: Найти 13-ую производную функции y-sin i.
Если есть производная от второй производной, назовите ее третьей производной, » (Или / «‘(*), 0, …), поэтому y’ 1 = (y ») Людмила Фирмаль
Если есть производная от второй производной, назовите ее третьей производной, » (Или / «‘(*), 0, …), поэтому y’ 1 = (y ») ‘. N-ая производная (или n-ая производная) является производной (n-1) -ой производной. у ^ = Следующая производная на первой называется производной высшего порядка. Начиная с 4-й производной, производная обозначается римской цифрой или числом в скобках (yv или 5-я производная) Пример: Найти 13-ую производную функции y-sin i.
y ‘= (sin a :)’ = cos x = sin ^ a; + ^, y «= [y ‘)’ = (cos x) ‘= -sin a; = sin ^ a; + ~ • y'» = (-Sin x) ‘= -cos x = sin ^ a; 4- ~ y / v / = (-cosж)’ -sin x-sin ^ x Механическое значение второй производной Перемещайте массу M линейно по закону S = -f (t). Как уже известно, производная S’t равна скорости точки в данный момент времени: S [~ V. Вторая производная траектории по времени указывает на ускорение линейного движения точки, то есть S «= a.
| Дифференцирование функций, заданных неявно и параметрически | Дифференциал функции и его геометрический смысл |
| Логарифмическое дифференцирование | Основные теоремы о дифференциалах. Таблица дифференциалов |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В определенное время t скорость в определенное время равна Y, а в определенное время t • + ■ скорость равна V 4 -ДV, то есть скорость изменяется на величину AV за период времени. Соотношение представляет собой среднее ускорение точек Время. Этот предел отношения в At 0 называется ускорением точки M в данный момент t и обозначается буквой a. lim 4rr = a, т.е. V ‘= a. D £ -> o At Но V = S’t. Следовательно, a = (SJ) ‘, то есть a = S’t’ 3.
Неявно обозначенные производные высшего порядка функция Дифференцирование этого уравнения по a и решение результирующего уравнения по y дает первую производную (первую производную). Дифференцирование первой производной rio x дает вторую производную неявной функции. x> y и y ‘включены. Подставляя уже найденное значение y во второе производное выражение, выразите y через x и y. Действуйте аналогичным образом и найдите производные третьего и более высокого порядка.
Предположим, что функция y = f (x) неявно задана в виде F (x; y) = 0. Людмила Фирмаль
Пример: если x 2 + y2 = 1, найдите y ‘». Дифференцируйте 4 уравнения x2 4-y2-1 = 0 по x: 2x 4 2y • y1 = 0. Отсюда? / ‘= Далее, у «= -1’ ^ ‘^, т.е. у’ ‘= в у2 4-х2 1, 2 I 2 1 \ = —- r— = ——— (после ar 4 • y = 1), поэтому Уу w — 1 • 3y2 • y1 3 / x \ gx. Очевидно, y ‘»= —- = • (-) = -. ♦ U U4 U ‘U5 Производные высшего порядка от заданной функции параметрический Дайте функцию y =} (x) как параметрическое уравнение у = у (т). Как известно, первая производная y’x имеет вид 4 = ff • (i) х
Найти вторую производную функции, заданную параметрически. Из определения второй производной и уравнения (1) y’L = W’r = t’x = X \ Это YXX-G (2) х Точно так же получите следующее /// _ (VxxYt iv _ (‘y’xxxYt UXXX / ‘UXXXX I «Xt x = cos y = sin £. Пример: Найти вторую производную функции ♦ Tso выражение (1) , _ (Sinf) J _ cos £ _ Далее формула (2)Обратите внимание, что y e x можно найти из преобразованного jurmule (2). Uhh <A K) 3 Есть небольшая ценность, чтобы помнить.

