Оглавление:



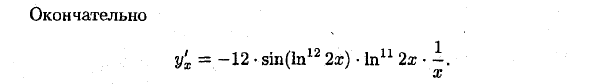
Таблица производных
- Производная таблица Производные правила и формулы для производных основных примитивных функций в табличной форме. На практике часто бывает необходимо найти производную сложной функции. Таким образом, в приведенной ниже дифференциальной таблице аргумент «x» заменяется промежуточным аргументом «и». 1. Правила дифференциации 1. (u ± v) ‘= и’ ± v ‘\ 2. (u-v) ‘= u’v + uv \ Особенно (si)’ 3. (s) ‘= u’v-uv ^ Особенно (J)’: 4. Если y = x («), y’x-y’i ‘их> и = yi = если 2 / = / (x) и x = = s • u
(с) ‘= 0; 2. (u «) ‘= a • ua к r • u’, особенно {y / u) ‘= ^^’ и ‘\ 3. (ai) ‘= ai • a • и’, особенно (ei) ‘= ei • и’; 4. (loggy gy) ‘= —m— • и’, особенно (В и) ‘= — • и «\ 4» и • В 4 »и 5. (sin and) ‘= cos and • and’; 6. (cos and) ‘= -sin и • and’; 9. (arcsintx) ‘= —y * ■ • и’; 10. (arccosu) ‘= -> * ■ • и’; V1-u2 \ / 1-u2 11. (arctgu) ‘= j- ^ s • и’; 12. (arcctgw) ‘= -— C • и’; 1 4 и 1 и 13. (sh и) ‘= ch и • и’ \ 14. (ch and) ‘= sh и • и’; 15. (th и) ‘= -A- • 16. (Cth и) ‘= —4- • и’. v ‘ch2 и sh2 и Чтобы вычислить производную, вам нужно знать только основные фундаментальные производные правила и формулу производной, и строго соблюдать эти правила при выполнении упражнения.
Дифференциальная формула 1. Людмила Фирмаль
| Производные основных элементарных функций | Дифференцирование функций, заданных неявно и параметрически |
| Гиперболические функции и их производные | Логарифмическое дифференцирование |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Пример: Найти производную функции: 1) 2 / = π4-3×3 + 2x-1. ♦ у ‘= (х4-Зх3 + 2х-1)’ = (х4) ‘- (Зх3)’ + (2®) ‘- (1)’ = 4а: 3-З (х3) ‘+ 2 (х) ‘-0-4×3 ~ 9×2 +2. ♦ Вы должны стараться не оставлять ненужных записей. 2) Y = _ 2×3 TGX ‘ v- / 2a; 3y_2 (a3) ’-tgx-x3- (tgx)’ = 2 3i2-tgi Vte® / (tg a;) 2 (tgx) 2 Производная была найдена. Ответ не упрощен. В процессе решения правил 2 и 3 и уравнений 2 и 7, 3) y = cos (ln12 2x). ♦
Сокращенное решение: y1 = -sin (ln12 2x) • 12 In11 2x •• 2. Решение с объяснением: эта функция может быть выражена как: y = cos u, и — * 12, t = In g, 2 = 2x. Найти производную комплексной функции по правилу y’x-y’i-u’t • t’z • z’x (здесь есть три промежуточных аргумента). t / i = -sin w • 12 • t11 * — • 2 Z y’x = -sin * 12 • 12 • (z) n ‘^’ 2 y’x = -sin (ln ^) 12 • 12 • In11 z • -, х 2 / i = -sin (ln12 2x) • 12 • In11 2x • i. _ _C08 * X Это Это
Это в конце концов y ‘= -12-sin (in12 2s) • In11 2s • i. s Людмила Фирмаль

