Оглавление:
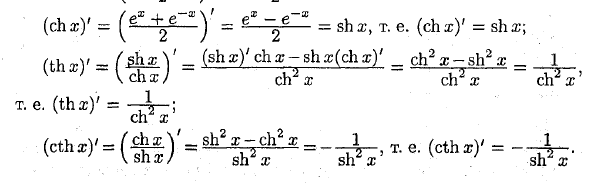
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
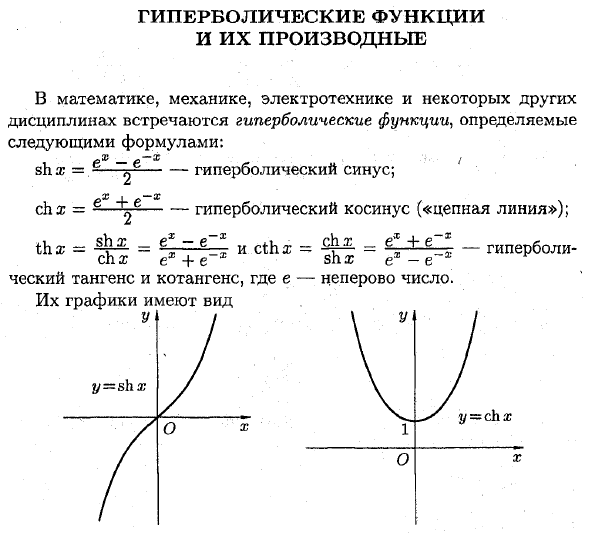
- Гиперболическая функция и ее производные В математике, механике, электротехнике и других областях существует гиперболическая функция, определяемая как 25- ■ X sh x = электронный гиперболический синус;
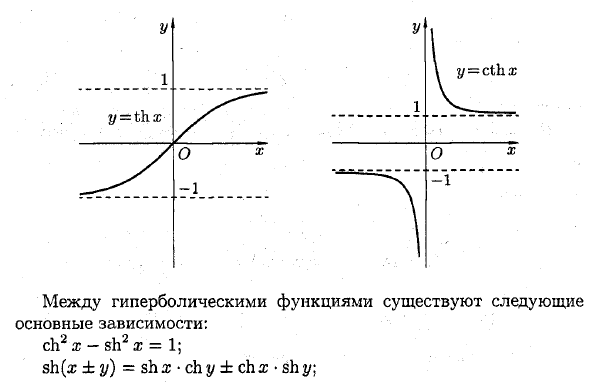
th * = te = и cth3: = w = — ™ переболи- касательная и котангенс. е не-число.Y 1 Y 1 ™, у = спасибо! / 0 х 0 * -1 __ -1 \ Существуют следующие основные зависимости между гиперболическими функциями. ch2 x-sh2 x = 1; sh (s ± y) = sh x • ch y ± ch x • sh
C I-x chx = 6 y — гиперболический косинус («цепная линия»); Людмила Фирмаль
| Производная сложной и обратной функций | Таблица производных |
| Производные основных элементарных функций | Дифференцирование функций, заданных неявно и параметрически |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
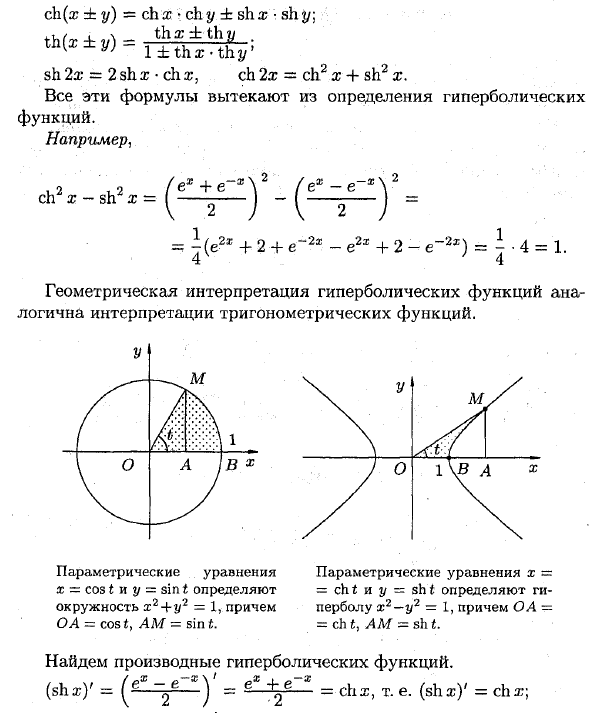
- ch (rc ± y) = ch x • ch y ± sh x • sh y \ sh 2x = 2 sh x-ch x, ch 2x = ch2 a; 4-sh2 a; Все эти формулы основаны на определении гиперболической функции. Например ex-e ~ * \ 2 V 2 J \ 2 J = 1 (e2l + 2 + e to 2®-e2r + 2-e «2») = L ■ 4 = 1. 4 4 .2 _ ch a: -sh x = Геометрическая интерпретация гиперболических функций аналогична интерпретации тригонометрических функций.
Параметрические уравнения x = cht и y = sht определяют гиперболу x2 — y2 = 1, OD = ch t, AM = sh t. Найти производную гиперболической функции. (Shx) ‘= (eX ~ 2e’X)’ = e * Y «= cbd, т.е. (shxY = chx \ Параметрические уравнения x = cos t и y = sin t определяют круг x2 + y2 = 1, а OA = стоимость AM = sin t.(ChxY = («‘+» *)’ = от -BD до 2e X = shz, т.е. (ch®) ‘= shx; ф? V = V = (ша?);
Чар-ша; (ch ar) ‘_ ch2s-sh2a; = 1 V} h chx / dr2 ^ ch2 *’ То есть (thz) ‘= -A-; ч ж (Cthxy ‘= fY’ = sb2x-ch2x = _ 1 т.е. (cthx) ‘— X-.v; Vshz / sh2®sh x v / sPx Людмила Фирмаль

