Оглавление:



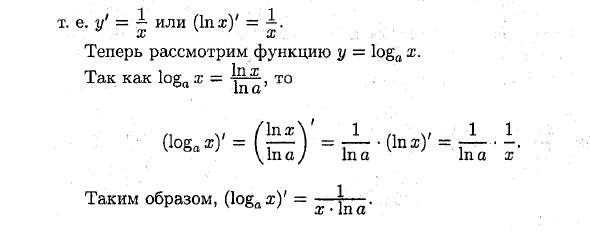



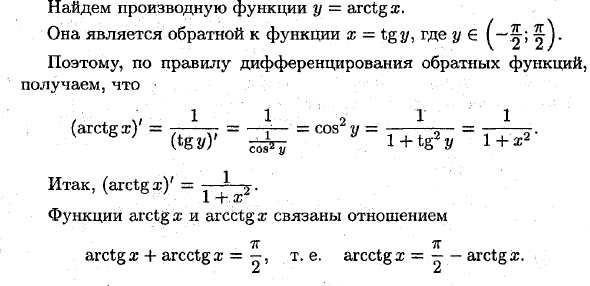


Производные основных элементарных функций
- Производные основных элементов функция 1. Степенная функция y = xn, производная от n∈N Дайте аргументу x приращение Ax. Функция y = xn получает приращение Ay = (x + Ax) n-xn. Бином Ньютона, Dm / = (xn + n • xn до 1 • dx + n (/ 127 1) * n до 2 • Ax2 + •• + (dz) n) -xn = n • x «-1 • Ax + n (I 7 1} x «» 2Ax2 +. • + (Ax) n. тогда Да _ да •• Да: + ^^ xn-2Ax2 + — + (Топор) n Ах Да: = n • x ^ 1 + P (A27 1} • x «~ 2 ■ Ax + … + (yes)» — 1. Найти предел отношения, составленный с Dx 0. lim lim fn.xn «4in. (ri-l) -xn-2Ax +. • + (Dx) и» A Dx-> oDx Ax-> 0 \ 2 v) Вот так {xnY = n-xn ~ 1. Например, (x3) ‘= 3×2, (x2)’ = 2x, x ‘= 1.
Ниже (см. Примечания) мы покажем, что производное выражение степенной функции справедливо для любого η∈E (не только натуральных чисел).♦ найти у: Y ‘= \ ■ 2 * + (-2) * «3 + O, То есть y ‘= x —K. Подставьте значение y в следующую формулу:
х X * ‘(от X до Js) + 1 = x *> t’e’ + 1 = 0 = 0 Функция удовлетворяет этому уравнению. Людмила Фирмаль
Экспоненциальная производная y = a®, a> 0 и Φ1 Сначала найдите производную функции y = ex. Если вы укажете приращение Ax для аргумента x, вы можете увидеть приращение функции Au. Au = ex + Ax-e * = e * (eAx-1). Так что ^ = и .. Au x eAh-1 lim -7— = lime ■ •> —— = — J-> 0 Да: d®-yaAh ааа-1 ах = ex • lim- = e * • lim = ez -1 = e *. Dh — fO Ах Dh-> o Да:При расчете пределов мы использовали эквивалент ex-1 для x для x 0. Следовательно, y ‘= ex, то есть (Пример) ‘= e *. Теперь рассмотрим функцию y = ax, x € R.
Поскольку ax = elIna, используя производную формулу комплексной функции, (Ax) ‘= (ex ln a)’ = ex Jn a • (x • In a) ‘= ln a • In a = ax • In a. Следовательно,> (a1) ‘= ax In. Пример: Найти производную функции y = от 7x до 4g. ♦ Использование сложных производных функций и степенных производных y ‘= (7 * 2-4 *)’ = 7g2-4zh • In 7- (g2-4®) ’= 7×2-4 * • In 7 • (2x-4). ♦ 3. производная логарифмической функции y = loga x, a> 0 и Φ1 Сначала найдите производную функции y = In x. Для нее Ay = In (a; + Da?) — In x = ln (t) = 1n (1 + Lx Топор Топор Топор Передайте предел как Ax-> 0 и используйте эквивалентный ln (l + ~ как Ax 0, чтобы получить: A y b (14- ^ r 1 1 LIRN- ■ =. lim ———— = lim = lim — = -, Dx-> 0 Axe Dx- * 0 Axe Ax-> 0 Axe Dx- * 0 X X
| Производная суммы, разности, произведения и частного функций | Гиперболические функции и их производные |
| Производная сложной и обратной функций | Таблица производных |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- е. y ‘= J или (In®)’ = i. Теперь рассмотрим функцию y = loga x. logrt x = тогда (Logaa) ‘= jTTna * Пример: Найти производную функции y = ln (®4-2®3 + b). Производная логарифмической функции y = logrt® может быть найдена различными способами. Его обратное значение равно x-ay}, поэтому уравнение обратной производной дает (Журнал «х)» = 1 1 1 ((Y ay- \ pa a: -In a ‘ 4.
Для функции y = sin®: Ay _ sin (® -> — A®) -sin® 2 sin ^ -cos (® + _ sin / Д®Л A® ~~ D® ~ D® ®®-4 Предел 0 достигнут с использованием первого значимого предела ^ d ^ 3 = ^ Ай грех ^ (Ах \ lim- = lim- • cos x + — = 1 c.os Dx-> o Ax Dx-> 0 ^ V 2 / L / То есть y1 = cos® или (sin®) ‘= cos®. Найдите производную функции y = cos®, используя выражение комплексной производной. (Cos®) ‘= (sin (| -®)) = cos (~ -®) • -®) =. ‘ = cos (^ — • (-1) = -sin®,
Производные тригонометрических функций y = sin®, y = cos®, y = tg®, y = ctg® Людмила Фирмаль
То есть (cos x) = -sin x. Чтобы найти производные функций y = tg x и y = ctgx, используйте выражение производной по частям. , _ / SinxV _ (sin a;) 7 cos a; -sina; (cosx) ‘V cos x J cos2 x cos’2 x -f sin2 x 1 cos2 x cos2 x ‘ То есть (тга;) ‘= -. потому что X Сделав ту же операцию, получите выражение 1 грех2 х (Ctg x) ‘= Этот результат можно получить разными способами.
Пример: (cos 2a 🙂 ‘= -sin 2x • (2x)’ = -2sin2x. 5. Дифференцирование обратной тригонометрической функции y = arcsina:, y = arccosa:, y = arctga:, y = arcctga: y = arcsina: Обратная функция имеет вид x = sin y и представляет собой интервал («» 2 * 2) veRH0 уравнение x ‘= cos yΦ0. По правилам производной обратной функции (Arcsina 🙂 ‘= (Sin y) ‘cos y y / i _ sin2 y VI-x2’ cos y> 0 для y £ («» § «§), поэтому знак плюс ставится перед маршрутом. • (arcsina 🙂 ‘= Точно так же, (arccosa 🙂 ‘= -y * Эта форма а: 2 Лу легче достать: arccosa: + arcsina: = т.е. / ч / 7YY + Дуга arccosa: = tj-arcsina:, затем (arccosa 🙂 ‘= ^ -arcsina 🙂 = -, *
Найти производную функции y = arctan x. Это обратная функция x = tgy. Где у € Следовательно, согласно правилам дифференцирования обратной функции, (Arctgx) ‘= w = i ^ = r- ° sV = ^ = rh- Следовательно, (arctg x) ‘= * h. 1 « T » X Arctg работает о. И дуги связанные; arctg x + arcctg x = то есть arcctgx = ^ -arctg x. Различая это равенство (Arcctgx) ‘= -arctgxj = — (arctgx)’ = — Т.е. (arcctga;) ‘= — * l. 1-е-х Пример: 1) (arccosa: 2) ‘= —- • (x2)’ = г / 1 — (* 2) 2 г / т ^ х ** х 2) (a: • arctga 🙂 ‘= x’ ♦ arctga: + x- (arctga;) ‘= arctga: H ——— 2, 1 + х 3) ((1 + 5x-over: 3) 4) ‘= 4 (1 -f 5a: -3×3) 3 ■ (5-9×2); 4) (arccosу / х) ‘= •’ 5) (log3 (3 + 2 ~ x)) ‘= 3 log2 (3 + 2-) • (3 ^ 21х) 1п3 ■ 2- • In 2 • (-1). Примечание.
Найдите производную функции y = xa, которая должна иметь любой показатель степени a∈K. В этом случае предполагается, что функция x> 0. Вы можете написать xQ = eaLnx. Из-за правил дифференциации сложных функций, (X *) ‘= (eaLnx)’ = e * Ln x • (a • In x) ‘= a • ea, n *. — = a • — = a • x «» 1 Х х То есть (ха) ‘= a • Xy «1. Если функция x <0, выражение остается в силе. y = xQ существует: Для всех xΦ0. L j Пример: функция y = -f; rC-4-C является выражением x3 •? / + 1 = х4 выполняется.

