Оглавление:

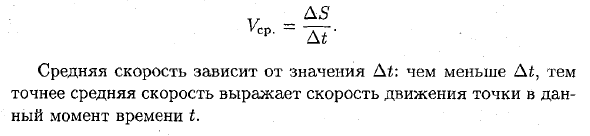



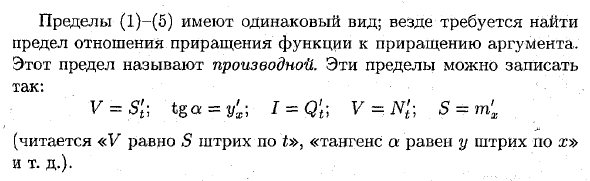
Задачи, приводящие к понятию производной
- Задачи, которые приводят к понятию производных Понятие дифференциации является одним из основных математических понятий. Производные широко используются для решения многих задач в математике, физике и других науках, особенно при изучении скорости различных процессов. 1, линейная задача скорости движения • ч Заставить материальную точку (тело) М двигаться неравномерно.
Некоторые прямые. Каждое значение времени t соответствует определенному расстоянию OM = 5 от определенного расстояния O до определенного расстояния O. Это расстояние зависит от прошедшего времени t. То есть 5 = 5 (0. О_М Мл я S (т) 1 Нужно найти скорость по точкам. Если точка занимает позицию M в определенный момент времени t, то эта позиция занимает позицию Mi в момент времени t -f At (At — это приращение времени).
Это равенство называется законом точечного движения. Людмила Фирмаль
Где ОMi = 54-Д5, где AS — приращение расстояния. Следовательно, смещение точки M за время At равно AS = S (t + At) -S (t). Перед Соотношение представляет среднюю скорость точек во времени.Средняя скорость зависит от значения At: чем меньше средняя скорость, тем точнее скорость точки в конкретный момент времени t.
Ограничение средней скорости движения, когда временной интервал D * стремится к нулю, называется скоростью точки (или мгновенной скоростью) в конкретное время. Выражая эту скорость в V, т / гЛ5V = Iim-, D £ -> 0 ат (I) V = lim о или S (t + At) -S (t) At 2. Кривая касательной проблемы Во-первых, вот общее определение касательных кривой: Возьмем две точки M и Mi непрерывной кривой L. Прямая ММ, проходящая через эти точки, называется секущей.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Точка M \, которая движется вдоль кривой L, движется как можно ближе к точке M. Во-вторых, секущий, который проходит вокруг точки Mu, стремится к определенной предельной позиции MT. Касательная к данной кривой в данной точке M является предельной позицией MT секущего MMj, проходящего через точку M, когда второе пересечение M \ приближается к точке M \ вдоль кривой бесконечно. Теперь рассмотрим график непрерывной кривой y = f (x) с не вертикальной касательной в точке M (x] y). Найти его угловой коэффициент k = tga. Где a — угол касательной к оси OX.
Для этого используйте горизонтальную секцию g ++ A, чтобы нарисовать точки через точки M и Mi на графике. Указывает угол между секущим MM \ и осью Ox как ip. На этом рисунке показано, что коэффициент секущих углов равен sec = = d ^ s. _ / (W + Dar-f (x) ахВ случае Ax 0 приращение Au стремится к нулю из-за непрерывности функции.
Для этого используйте горизонтальную секцию g ++ A, чтобы нарисовать точки через точки M и Mi на графике. Людмила Фирмаль
Следовательно, точка M \ бесконечно близка к кривой к точке Af, а секущая MM \ вокруг точки M является касательной. Угол (p-> a, то есть lim
0 Следовательно, касательный наклон A; = tg a = lim tg > = Иш лим + (2) , Топор-> 0 Топор—> 0 Топор Dx-> 0 Топор x Открытие форм (1) и (2) приводит к решению и многим другим проблемам. Вы можете показать, что: Если -Q = Q (t) — количество электричества, проходящего через поперечное сечение проводника в течение времени t, сила тока в момент времени t / = Iim * 9. = Lim Q (t ^ t) -Q (t) At-At At * -> 0 At
Если -Лг = N (t) — количество вещества, которое вступает в химическую реакцию в момент времени t, то скорость химической реакции в момент времени t равна v = lim ™ = lim (4) At- * o At & t-> o At Если -m = m (x) — неоднородная масса стержня между точками 0 (0; 0) и M (x; 0), то линейная плотность стержня в точке x равна I 5 = lim ^ = Ish «(* + *) -» (). (5) Аз-> Q Топор Топор- ^ 0 Топор
Ограничения (1) — (5) в том же формате. Все места, где необходимо найти ограничение на отношение приращения функции к приращению аргумента. Это ограничение называется производной. Эти ограничения могут быть записаны как: V = S’t \ tga = y’x \ I = Q’t \ V = S = m’x («Y равно S» — это «простое число t», «касательная a — простое число в x» и т. Д.).

