Оглавление:

Свойства функций, непрерывных на отрезке
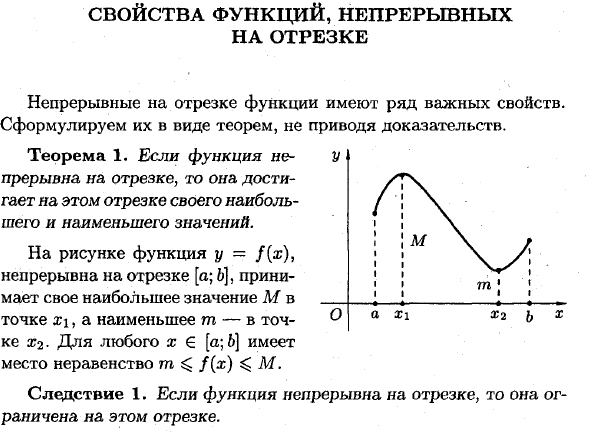
- Характеристики непрерывной функции Функция, которая продолжается в сегментах, имеет несколько важных свойств. Сформулируйте их в виде теоремы без доказательства. Теорема 1. Если функция непрерывна в сегменте, то максимальные и минимальные значения достигаются в этом сегменте.
Любое неравенство x € [a; B] есть m ^ f (x) ^ M. Следствие 1. Если функция непрерывна в сегменте, она ограничена в этом сегменте.
На рисунке функция y = f (x) непрерывна в интервале [a;. 6], предполагая максимальное значение M в точке x \ и минимальное значение m в точке X2. Людмила Фирмаль
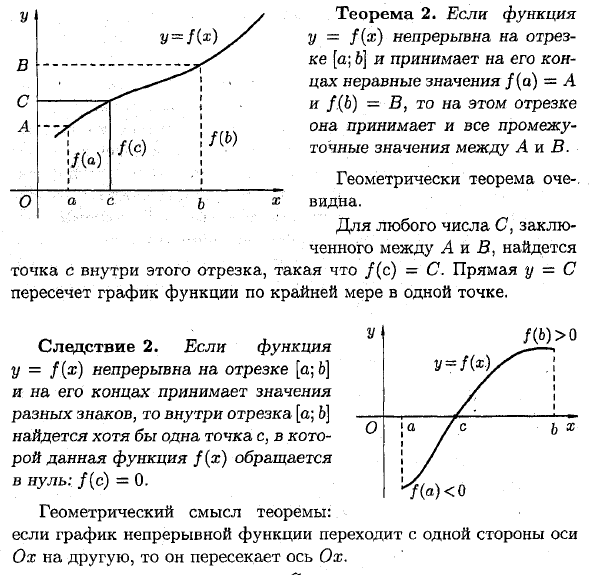
Теорема 2. Функция y = f (x) берет интервал [a; 6] и принимает неравные значения f (a) = A и f (b) = B на обоих концах, а также на этом отрезке A и B Возьмите все промежуточные значения между ними. Геометрически теорема ок. О, я вижу х. Для любого числа C между A и B в этом сегменте есть точка c, где / (c) = C. Прямая y-C пересекает график функции хотя бы в одной точке. 7 (а) <0
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Результат 2.Функция> y = f (x) непрерывен в интервале [a; Есть по крайней мере одна точка c, которая принимает различное значение знака на обоих концах B], а затем исчезает заданная функция f (x) в сегменте [a; B]: f (c) = 0. Геометрический смысл теоремы: когда график непрерывной функции проходит от одной стороны оси Ox к другой, он пересекает ось Ox.
Результат лежит в основе так называемого метода «половинного деления», который используется для нахождения корня уравнения f (x) = 0. Утверждения теоремы 1 и 2, как правило, ложны, если они нарушают любое из условий. Функция имеет интервал [a; 61 и интервал (a; b) или интервал [a; b] зазор. На рисунке это показано для следствия теоремы 2.
График разрывной функции не пересекает ось Ox. т> о Да) <0 Людмила Фирмаль

