Оглавление:


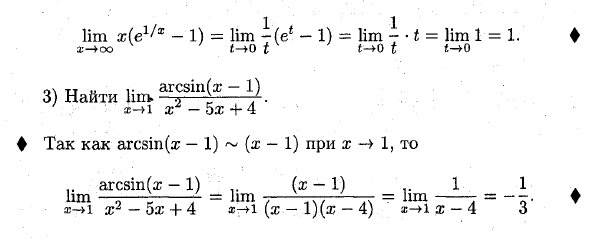
Применение эквивалентных бесконечно малых функций
- Бесконечное эквивалентное приложение Маленькая функция 1. Для расчета эквивалентного использования BMF предел Чтобы учесть неопределенность в форме g, часто удобно применять принцип замены бесконечно малых на эквивалентные эквивалентные бесконечно малые функции и другие свойства. Как известно, это sin x ~ x в x 0 и tgs ~ x в x 0.
♦ lim-x- = lim-5— = lirn ~~ • — ~ = 1-1 = 1. f r-> 0 si z-> 0 si »-» 0 £ | 2 2 SC- »o) 2 2 2. Найти lim arcsina; х—> 0 х ♦ обозначает арксину. = т. Затем t = 0 для x = sin £ и x 0. Таким образом, arcsina; .. т т. 1 1 lim- = lim-—- = lim -j — r = — = 1. x-> 0 F HO Sint t-> 0 щель 1 Следовательно, арчина; 0. ♦
Эквивалентный пример BMF __ «2 1. 1-cos a: указывает, что ~ \ как x 0. , .. 1 cos x 2 sin21 грех я грешу я Людмила Фирмаль
\ 1 + + x-1 до ~ отображаются как x-> 0. ♦ и позже v s / TTx-1 .. (y / TTx’-l) (y / l + x + l) lim —— lim ———. — = | * -> о | (Vl + ar + 1) r ■ _x y 2 2 = lim ^,. …— = лим. — = — = 1 | (Vi + ® + l) + 1 2 TO y / l + x-1 ~ ^ X 0, ♦ Ниже приведены наиболее важные эквиваленты, используемые при расчете пределов. 1. грех x ~ x при x 0; 6. ex-1 ~ x (x 0); 2. tgx ~ x (x 0); 7.ax-1 ~ x ■ in (x 0); 3. arcsinx ~ x (x 0); 8. ln (l + x) ~ x (x 0); 4. arctgrr ~ x (x-t 0); 9.loga (l + x) ~ x-logQ e (x-> 0); 5.1-cosx \ (x 0); 10. (1 + x) k-1 fc> 0 (x 0); В частности, y / T + ˜x-1˜1-bm |.
Пример: 1. Поиск лим ^ фф ^ ф. r r x-> 0 единица измерения: ♦ tg2a: ~ 2a: Позже, грех Over: ~ Over: при a: 0, затем tg2z ‘.2®2. Rim. o = lim- = f x — sin over: ®-> o over: 3 2) Найти lim ^ (e1 / * -1). х—> оо ♦ 4 = т. Продолжает с xoo до t 0. Таким образом, хlim x (e1 / x-1) = lim-leb-1) = lim — t = lim 1 = 1. x-> oo t-y0 t 0 t HO 3) Найти лим. ^ «jf» 1) 1 • x—> i xz-5zh 4-4 ♦ Для дуги (x-1) — [x-1) для x1, arcsinfa; -1) (ш -1) .. 1 1 lim —T) — = — r to lim 7-777-77 = нм— = — x-> l-ozh + 4 (w-1) (w-4) x- + i x-4 3
| Сравнение бесконечно малых функций | Непрерывность функций |
| Эквивалентные бесконечно малые и основные теоремы о них | Точки разрыва функции и их классификация |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
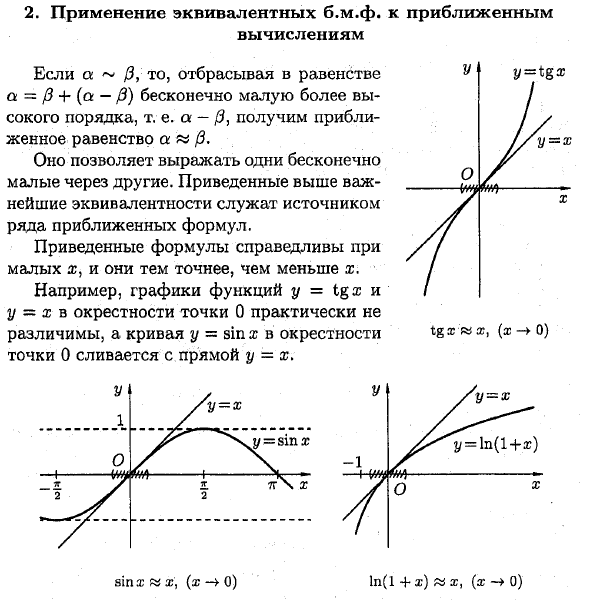
- Приблизительное использование эквивалента BMF расчет у-TGA? тгз «х, (х-> 0) ln (1 4th) «X, (x 0) Если a ~ 0Y, то уравнение a = / 3 + (a-0) получает бесконечно малый высший порядок, то есть a- (3, приближенное уравнение a / / 3). Это позволяет вам выразить некоторую бесконечную малость через других.
Наиболее важные из приведенных выше эквивалентов служат источником многих приближений. Приведенная выше формула справедлива для малых значений i и более точна при меньших значениях x. Например, графики функции y = tanz и y = x вблизи точки 0 практически неразличимы, а кривая y = sin x вблизи точки 0 совмещается с прямой линией y = x. у = смх грех х «х \ (х 0)
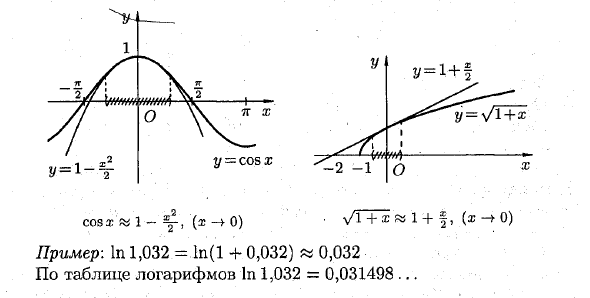
Пример: В 1,032 = ln (l + 0,032) «0,032 логарифмическая таблица, 1,032 = 0,031498 … Людмила Фирмаль

