Оглавление:

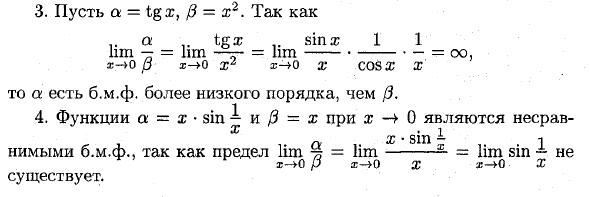
Сравнение бесконечно малых функций
- Сравнение бесконечно малых функций Как известно, сумма, разница и произведение двух bm.f. Есть бесконечно маленькие функции. Соотношение двух BMF может вести себя по-разному: это может быть конечное число, это может быть бесконечно большая функция, она может быть бесконечно малой или может быть неограниченной. Два BMFs сравниваются друг с другом через их отношения.
Предположим, что c * = a (x) и p- / 3 (x) являются b.f. как x- * xq}, то есть lim a (x) = 0 И lim P (x) = 0. х-> хо 1. Если lim% = AΦ0, (A∈K), a и (3 называются бесконечно X- * XQ p Маленький в том же порядке. 2. Для лимЩ — 0, а есть X- * X0 P /? Выше чем. 3. Если lim% = oo, a называется еще меньше бесконечно X- + X0 P Низкий порядок / 3. 4. Если lim% отсутствует, a и / 3 называются несравнимыми ® ~> ®0P mi минута. Обратите внимание, что это те же правила для сравнения BMF с x ± oo, xxo ± 0.
| Первый замечательный предел | Эквивалентные бесконечно малые и основные теоремы о них |
| Второй замечательный предел | Применение эквивалентных бесконечно малых функций |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Пример ». 1. а = 3х2, f3 = 14а; Для х 0 это bm.f. Около 2 9 lim% = lim ‘/.->=’ Φ0, поэтому тот же порядок x-> o r x-> o 14ag 14 Б.М.Ф. Одинаковые порядки а и / 3 стремятся к нулю практически с одинаковой скоростью. 2. Установите a = 3π4 и f3 = 1x. Поскольку x-> 0, функция a является b.m.f. более 4 3 Так как lim% = limЩ- = limЩ- = 0, выше чем f3 x— »0 p x- * 0 7X X до i0 7
В этом случае BMF, однако, стремится к нулю быстрее, чем / 3.Установите a = txx, P = x2. с того времени a .. tgx sin w 1 1 And- = lim- ~ = игла —— = co. x- »0 p x-> 0 X1®-» 0 x COSX X То есть заказы ниже, чем BMF 4. Функции a = x • sin- и / 3 = x, поскольку x —► 0 нельзя сравнивать x ^ sin ^
Неявным bmf, предел lim% = lim— = lim sin ~ x-> 0 p x-> 0 X x-> 0 X Exist. Людмила Фирмаль

