Оглавление:

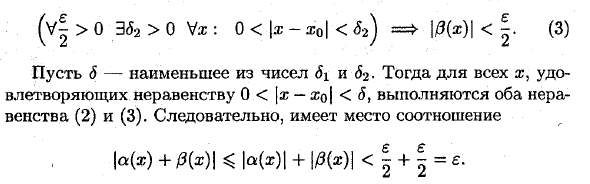



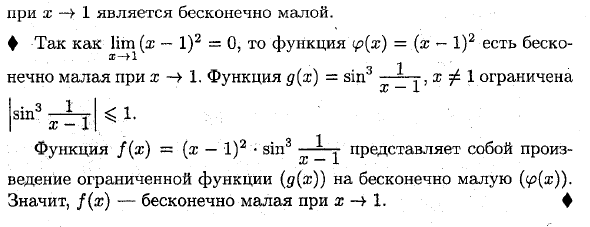
Бесконечно малые функции (Б.М.Ф.) и основные теоремы о них
- Инфинитезимальные функции (Б.М.Ф.) и их основные теоремы Функция y = f (x) называется бесконечно малой при x-> x0. lim f (x) = 0. (1) X-BHO По определению функциональных ограничений уравнение (1) означает: Для любого числа e> 0 неравенство 0 <\ x-xo | <справедливо для всех x я / (*) я <ж. Точно так же определяется BMF. как x-Y xo + 0, x xo-0, x + oo, от x до oo: f (x) 0 во всех этих случаях. Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми.
Обычно обозначается греческой буквой а, / 3 и т. Д. . Другой пример: xn = n∈N — бесконечная десятичная последовательность. Основная теорема о бесконечно малых. Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций является бесконечно малой функцией. <4 Пусть a (x) и f3 (x) — два часа дня. Функции как х- »х-. Это означает, что lim a (x) = 0, то есть e> 0, поэтому ~> 0 существует. <5i> 0 <неравенство выполняется так, что неравенство O <| x-xo | выполняется для всех x М *) 1 <| (2) lim, 3 (x) = 0, т.е. х-> х0
Пример функции BMF y = x2 при x 0; / = x-2 для x 2; y = sin x при x-> 7 Гк, k € b Людмила Фирмаль
(V |> 0 3S2> 0 \ / x: 0 <\ x-xol <62) ux) \ <(3) Пусть 6 будет минимальным числом, меньше 5-2. Далее, оба неравенства (2) и (3) выполняются для всех x, удовлетворяющих неравенству 0 <-x0 |. Следовательно, отношения | a (®) + P (x) \ <| a (; r) | + | / 3 (*) | <! +! = * •Вот так Ve> 0 38> 0 Va;: 0 <\ x-x0 | << 5 ==> \ a (x) + & (x) \ Xq. против ► Точно так же доказательство выполняется на конечном числе b.m. Функция. Теорема 2. Произведение ограниченных функций на конечные функции является бесконечно малой функцией.
Связанная функция М f (x) как x xq. Далее идут такие числа, как M> 0. 1/0) 1 ^ M (4) Все x-точки из 6 в окрестности точки a0 и a (x) равны b.m.s. когда х- »хо. Тогда если e> 0, то если jj> 0 Такое число 62> 0 является неравенством для всех x, удовлетворяющих неравенству 0 <μ-xq \ <62 M *) 1 <jj- (5) 6 показывает минимум Si и 52 числа. Далее для всех x выполнено неравенство 0 <\ x-xo | <S и оба неравенства (4) и (5). В результате | f (x) -a (x) | = | / (x) | • | a (g) | << jf ‘M = e. И это произведение f (x) -a (x) на x- »xq Есть бесконечно маленькие функции. ^ Следствие 1. Из всех бф.ф.
| Последовательности | Связь между функцией, ее пределом и бесконечно малой функцией |
| Предел функции | Основные теоремы о пределах |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Если он ограничен, его можно вывести из теоремы (2). Есть бесконечно маленькие функции. Результат 2. Продукт b.m.f. Есть бесконечно маленькие функции для чисел. Теорема 3. Частное деления бесконечно малой функции на функцию с ненулевым пределом является бесконечно малой функцией. / г / л «\ <lim a (ar) = 0 и lim f (x) = aΦ0. Функция A-4 W-4NW X- ¥ XQ J ¥ X) Из (x) и теоремы (2) об ограниченной функции η, представленной в виде произведения, является частное yjjj «= a (x) * to JJx) это FUNK * * IY бесконечно мало.
. Тогда есть 5> 0 на основе определения предела. Это неравенство 0 <| x-x0 | <6, неравенство | / (x) -a | | / (x) -a (= | a- / (x) | ^ | a | — | / (x) |, то; a | — | / (x) | <£, то есть | / (X) |> | a | — €> 0, поэтому 0), функция является бесконечной функцией и наоборот. Функция f (x) бесконечно велика, а j ^ j бесконечно мала. Пусть M a (x) будет bm.f. x- »x0, то есть lim a (x) = 0. Т.е. 1-4 ^ 1> ^ т.е. 1 a (g) I e » ‘a (x) X-> X0 (Vy> 0 35> 0 Vx: 0 <| x-x0 | | a (x) | <£, > M, где M = i. Это значит Функция j ^ Ly бесконечно велика. Также доказано Противоположное утверждение.
Указывает, что функция jj ^ j ограничена. е <[а | Людмила Фирмаль
► Примечание: доказательство теоремы было дано для x oo, но оно также справедливо для x oo. Пример: отображение функции Исправление) = (x-I) 2 • sin «1 х- 1 x-> 1 бесконечно мало. ♦ Поскольку lim (x-I) 2 = 0, функция ip (x) = (x-I) 2 бесконечно мала при x-> 1. Функция g (x) = sin3- = C-, x ^ I ограничена X 1 jsin3 <1. 1 х-1 _ Функция f (x) = (x-I) 2 • sin3-r Поддержание ограниченной функции ( (x)) Следовательно, f (x) бесконечно мало по отношению к x1.

