Функция

Оглавление:

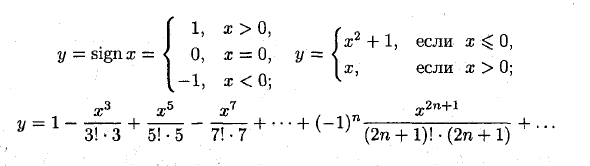
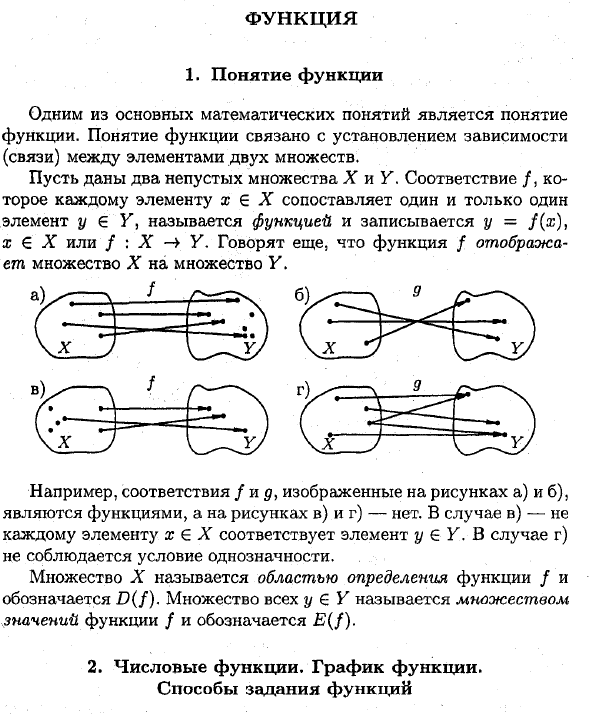
Функциональная концепция Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением связи (связи) между двумя наборами элементов. Дайте два непустых множества X и Y. Соответствие f, которое связывает один элемент x∈X только с одним элементом y∈Y, называется функцией и может быть записано как y = f (x), x∈X или f: X-> Y. Они говорят больше. Любая функция / дисплей

В случае c) -не все элементы x € X соответствуют элементам y € Y. В случае d) условие уникальности не выполняется. Множество X называется областью определения / и обозначается через D (f). Множество всех y∈K называется множеством значений /, обозначаемым ((/). 2. Числовые функции. Функциональный график. Как настроить функцию Комплексные функции Функция y = f (u) определена на множестве D, функция u = tp (x) определена на множестве D \ и около G

Например, соответствия f и q, изображенные на рисунках а) и 6), являются функциями, но не на рисунках с) и d). Людмила Фирмаль

Значение u = ip (x) 6D. Далее функция u = f (ip (x)) определяется в множестве D . Это называется комплексной функцией x (и суперпозицией некоторых функций или функцией функции) Переменная u = <p (x) называется промежуточным аргументом <составной функции. Например, функция y = sin 2x является суперпозицией двух функций y = sin и u = 2a;. Сложные функции могут иметь несколько промежуточных аргументов.

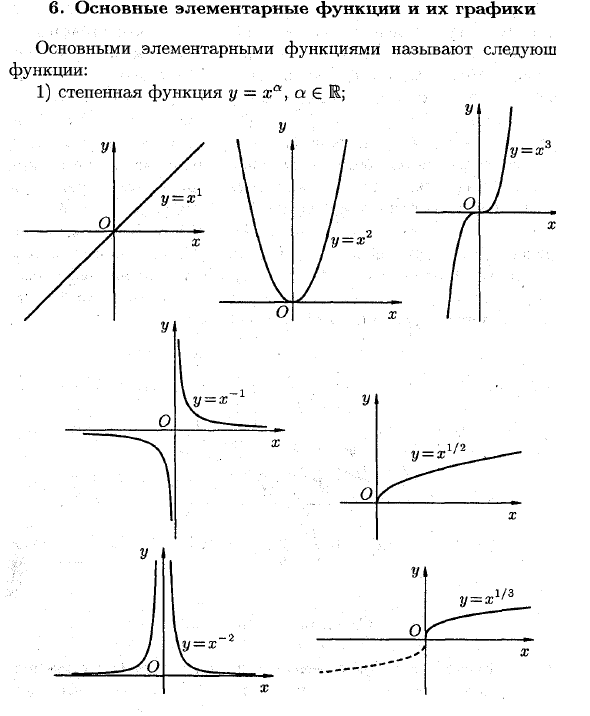
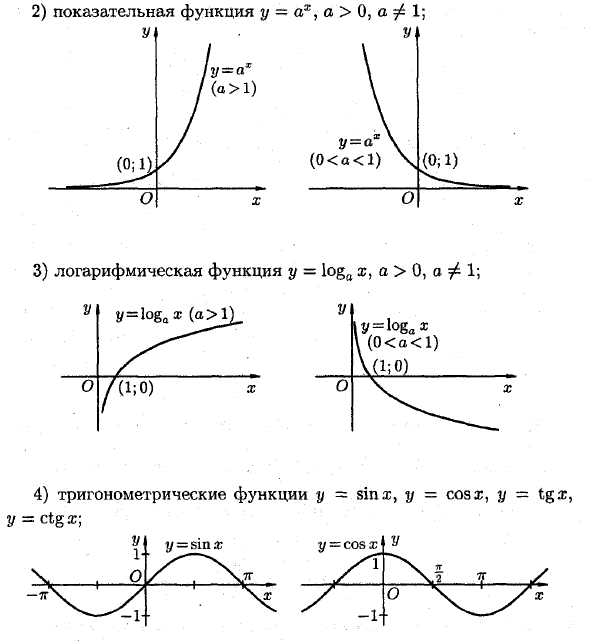
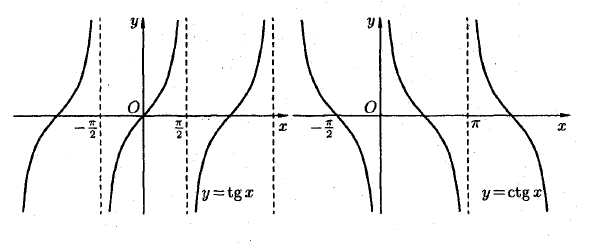
Основные основные функции и графика Основные базовые функции называются следующими функциями: 1) Степенная функция y = x0, a∈K; Y = x1 2) Экспоненциальная функция y = ax, a> 0 и φ1. Jy = az J (a> 1) y = a \ (0 0, оф1; у = бгакс 3) (0 <a <1) _ Логарифмическая функция у 4) Тригонометрическая функция y = sinx, y = cos x, y ~ tgx,

Решение задач по высшей математике

Канонические уравнения поверхностей второго порядка	Последовательности
Понятие множества. Логические символы	Предел функции

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

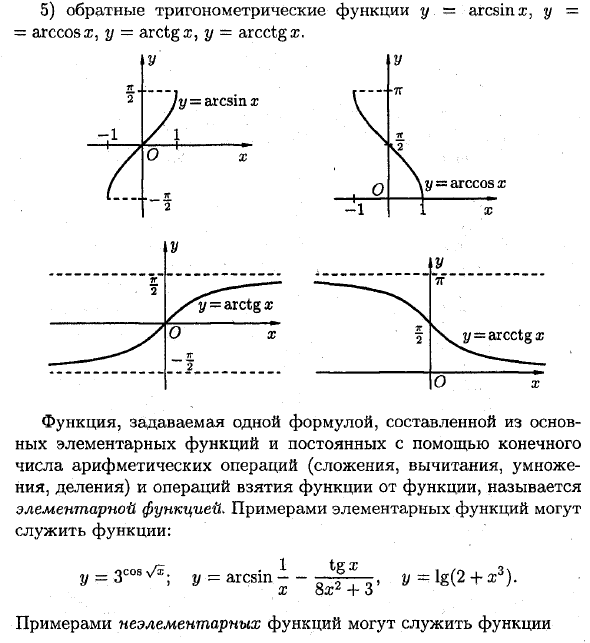
Обратная тригонометрическая функция y-arcsin x, y = да Грамм 2 7 г Ах х уу 2 зг 2 N ^^ — arcctg x Ох х Функция, определяемая одной базовой функцией и константой, которая использует конечное число арифметических операций (сложение, вычитание, умножение, деление) и операция, которая получает функцию из функции, является базовой функцией и Она будет называться.

Примером базовой функции является функция: „= 3 cosv / г. J, = arcsinI_y = log (2 + x3). Примером неосновной функции является функция R l, ®> o, Знак x = <0, x = 0, [-1, x <0; x3 i5 z7 ЗПз + 5Гб «7ГТ + ‘ x2 + 1 (если a); ^ 0, если x, r> 0; + (-1) «— +. ^; (2p + 1)! • (2p + 1) Y =

Функция f: дает X В дальнейшем мы будем изучать числовые функции (в принципе). Для краткости мы просто называем это функцией у = / (*) • В этом случае переменная x называется аргументом или независимой переменной, а y называется функцией или зависимой переменной (на x).

Если элементы множества X и Y являются действительными числами (то есть X C W и Y C E), функция / называется числовой функцией. Людмила Фирмаль

Что касается самих значений x и y, то они Функция зависит. Функциональная зависимость y от x может быть записана в виде y = y (x) без введения нового символа (/) для указания зависимости. Конкретное значение функции f (x) для x = a записывается в виде: / (a). Например, если} (x) -2×2-3, / (0) = -3, / (2) = 5.

График функции y = f (x) — это множество всех точек в плоскости Oxu, где каждый x — это значение аргумента, а y — соответствующее значение функции. Например, график для функции y = \ / 1-x2 представляет собой верхний полукруг с радиусом R = 1 с центром в 0 (0; 0). Чтобы указать функцию y = f (x) y, вам нужно найти соответствующее значение y и указать разрешенные правила. В большинстве случаев есть три способа настройки функции: анализ, таблица и графика. Метод анализа: функция определяется как одно или несколько выражений или уравнений. в ■ ^ v. m (x \ y) i \ у \ 1 1 -1 о * 1 х Пример: 1) S = nr2; 2) y = { 3) у2 ~ 4х = 0 х2 + 1, если х <2, х-4, если х ^ 2.

Если область функции y = f (x) не указана, предполагается, что соответствующее выражение соответствует набору всех значений аргумента, для которых это имеет смысл. Следовательно, домен [функции; 1]. Метод анализа для определения функции является наиболее совершенным, поскольку применяются методы математического анализа и функция y = f [x] может быть полностью исследована. Графический метод: График функции настроен. Во многих случаях графики автоматически составляются вручную

Появляется на устройстве или экране. Значение функции y y, соответствующее тому или иному значению аргумента x, можно найти непосредственно из этого графика. Преимуществом графического задания является его наглядность, а недостатком — неточность. Табличный метод: функция определяется последовательностью значений аргументов и соответствующей таблицей значений функций. Например, известная или логарифмическая таблица значений тригонометрических функций.

На практике следует использовать таблицу значений функций, полученных экспериментально или в результате наблюдений. 3. Основные функции 1. Даже если выполняются условия Vx ˆ D -x € D и f (-x) = f (x), вызывается функция y = f (x), определенная в множестве D. Нечетное число, если выполнены условия Vx € D -x∈D и f (-x) = — / (x). График четной функции симметричен относительно оси Oy, а нечетная ось симметрична относительно начала координат.

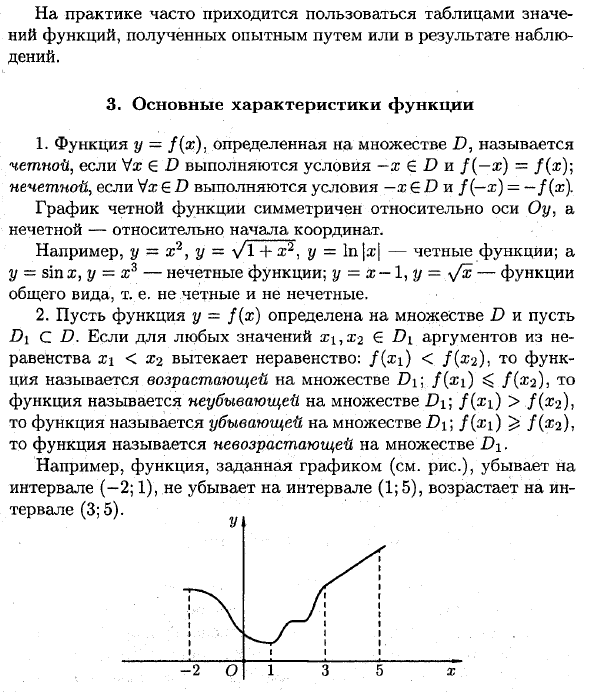
Например, y = x2, y = yr + x ^, y = 1n | x | — даже функция, y — это sin x, а y = x3 — нечетная функция. y = x-1,1 / = v ^ — это общая форма функции, то есть функции, которая не является ни четной, ни нечетной. 2. Определите функцию y = f (x) в множестве D, и функция D \ CD называется увеличением в наборе D \ \ f (xi) ^ / (x3), тогда функция находится в множестве Di / (Xi)> / (xr), функция называется убывающей с множеством D \;} (x ) ^ / (xr), функция называется невозрастающей с множеством >> я. Например, функция, указанная на графике (см. Рисунок), уменьшается с интервалами (-2; 1), не уменьшается с интервалами (1; 5) и увеличивается с интервалами (3; 5). х в -2 0 1 3 5

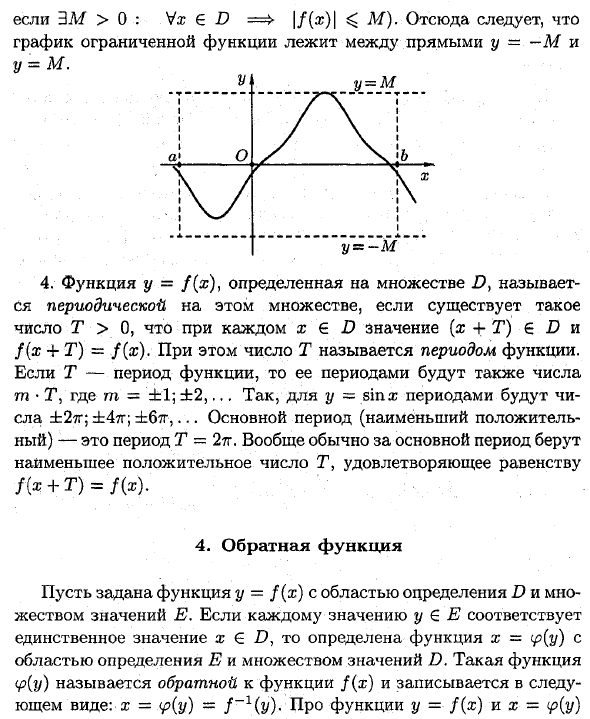
Растущие, не возрастающие, убывающие и неубывающие функции множества D \ называются в этом наборе монотонными, а возрастающие и убывающие функции строго монотонными. Интервал, в котором функция монотонна, называется монотонным интервалом. На рисунке (выше) функция строго монотонна при (-2; 1) и (3; 5). Монотонный (1; 3). 3. Функция y = f (x), определенная в множестве D, ограничена в этом множестве, если существует такое M> 0, что неравенство \ f (x) \ ^ M выполняется для всех x∈D.

(Краткое обозначение: y = f (x), x∈D называется ограниченным из D, Для 3M> 0: Vx 6 D = $> \ f (x) \ <M). Поэтому график ограниченной функции находится между y = —M строками и y = M строками. U y-M — ^; / \ И о / б N / V \ / L CHU 1 1 1 U-M 4. Функция y = f (x), определенная в множестве D, представляет собой значение (x + T) ∈D и f (x + T) = / (x) для каждого x∈D. Кроме того, число T называется периодом функции. Если T — период функции, период также является числовым значением m • T. Где m = ± 1. ± 2, …

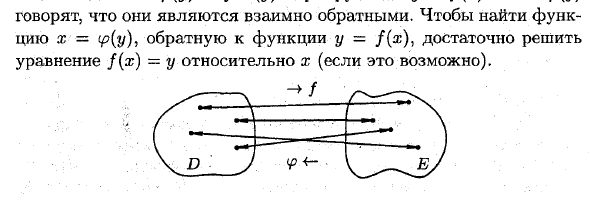
Поэтому, если y = sinx, период будет ± 27g. ± 47g; ± 67G, … основной период (самый низкий положительный период) — период T = 2tg. В общем случае основной период обычно принимает наименьшее положительное число T, которое удовлетворяет уравнению. / (* + M) = / (*). 4. Обратная функция Рассмотрим функцию y = f (x) с областью определения D и набором значений E. Такая функция <p (y) называется обратной функцией функции f (x) и записывается следующим образом: x = <p (y) = f ~ l (y). Для функций y = f (x) и x =

Говорят, что они противоположны друг другу. Для решения достаточно найти обратную функцию x = (p (y)> function y = f (x). Пример: ■ 1. Если функция y = 2x, обратная функция — это функция x = \ y. 2. Обратите внимание, что для функции y = x2 обратная функция x∈ [0; 1] имеет вид x = y / y . Функция y = x2 является интервалом [-1; 1], обратного не существует, потому что одно значение y соответствует двум значениям x (следовательно, y = тогда x \ = £ 2 = —

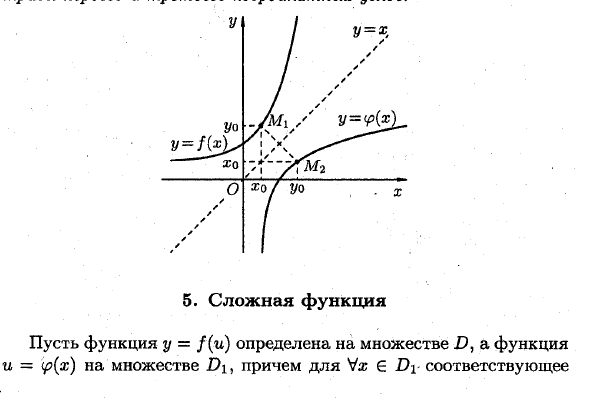
Из определения обратной функции функция y ‘= f (x) меняется на противоположную, только если функция f (x) определяет взаимно-однозначное соответствие между наборами D и E. Точная монотонная функция имеет противоположность. Кроме того, когда функция увеличивается (уменьшается), обратная функция также увеличивается (уменьшается). Функция y = f (x) и обратный x = (p (y) представлены одной и той же кривой, то есть их графики совпадают. Как обычно, независимой переменной (то есть аргументом) является x и зависимая переменная

Можно записать в виде y = ip (x), где y = f (x). Это означает, что точка Mi (x0 \ y0) на кривой y = f (x) становится точкой Mg (2 / o; £ o) на кривой y = v (x). Однако точки M \ и Mg симметричны относительно прямой y = x. Поэтому графики обратных функций y = f (x) и y = ip (x) симметричны относительно биссектрисы первого и третьего координатных углов.