Оглавление:

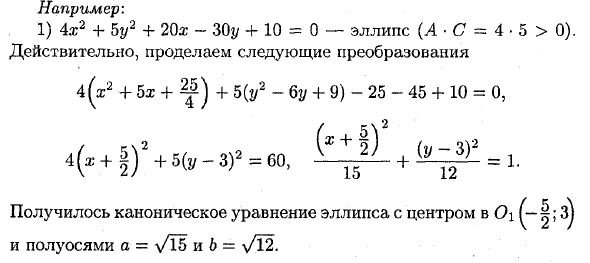
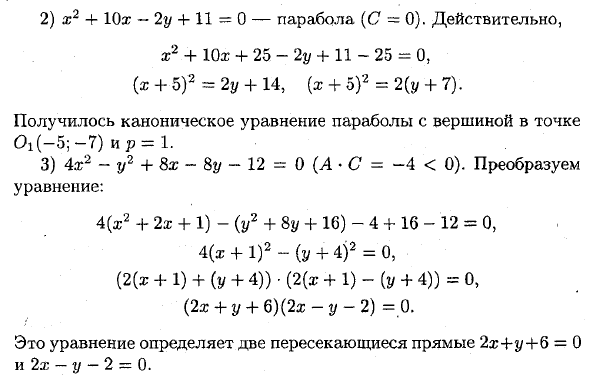
Общее уравнение линий второго порядка
- ОБЩЕЕ УРАВНЕНИЕ ЛИНИЙ ВТОРОГО ПОРЯДКА 1. Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям Найдем сначала уравнение эллипса с центром в точке О \ {хо] Уо)> оси симметрии которого параллельны координатным осям Ох и Оу и полуоси соответственно равны а и Ь.
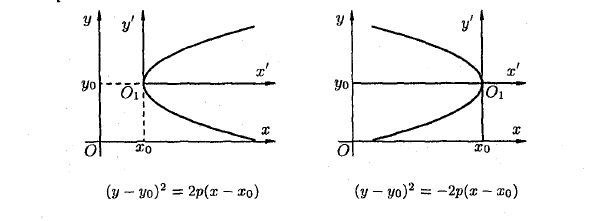
В этой системе координат уравнение эллипса / 2/2 X у ‘ + TS- = 1. а * Ь2 Так как х ‘= х-х0, у’ = х-у0 (формулы параллельного переноса), то в старой системе координат (а? ‘* о)’ 2, СУ-Уо) 2 , а2 б2 Аналогично рассуждая, получим уравнение гиперболы с центром в точке 0 \ (xq \ г / о) и полуосями а и: (* — ^ о) 2 (У ~ Уо) 2 _ -а2 б2 И наконец, параболы изображены на следующих рисунках. У ^ у ‘ ! Уо л X О Ох ^ — ^ X О Хо (у-УО) ‘2 = -хо) (у-УО) 2 = 2р (х-хо)
Поместим в центре эллипса Ох начало новой системы координат 0 \ х’у », оси которые 0 \ ХГ и 0 \ у ‘параллельны осмотрительны. Людмила Фирмаль
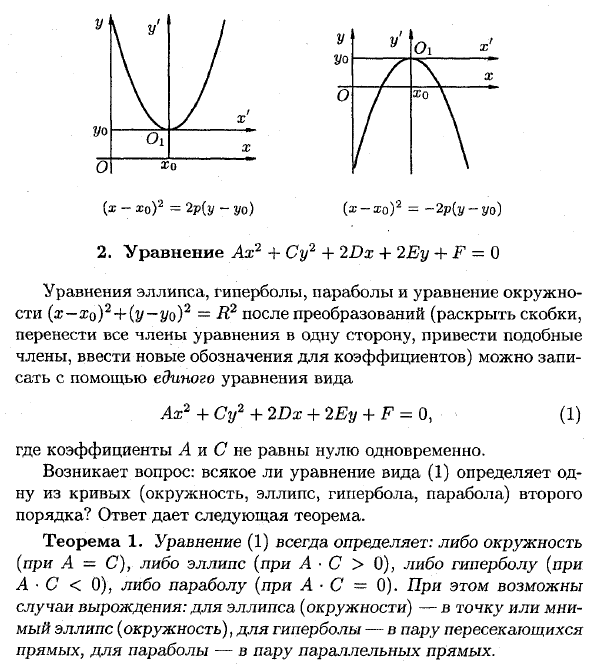
(а: -хо) 2-2р (у-у0) 2. Уравнение Ах2 + СУ + 2Da; + 2% + F = О Уравнения эллипса, гиперболы, параболы и уравнение окружности (х-хо) 2-е (у-уо) 2 — R 2, после преобразований (раскрыть скобки, перенести все члены уравнения в одну сторону, привести подобные члены, ввести новые обозначения для коэффициентов) можно записать с помощью единого уравнения вида (1) Ах2 + Су2 + 2 Дх + 2 Еу + F = О, где коэффициенты Л и С не равны нулю одновременно.
| Гипербола | Поверхности и линии в пространстве и их уравнения |
| Парабола | Различные виды уравнений плоскости в пространстве |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Возникает вопрос 😕 Всякое ли уравнение вида (1) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка Ответ дает следующая теорема. . Теорема 1. Уравнение (1) всегда указывает: либо окружность (при А = С), либо эллипс (при А • С> 0), лбо) При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (для окружения), для параболы в пару параллельных прым (х-хо) ‘2 = -2р (у-уо)
Например: 1) 4х2 + 5у2 + 20х-30у + 10 = 0-эллипс (А • С = 4 • 5> 0). Действительно, проделаем следующие преобразования я (х2 + 5х + ^ р) + 5 (у2-6у + 9) -25ф-45 4-10 = 0, Получилось каноническое уравнение эллипса с центром в 0 \ и полуосями а = и 6 = у / 12. 2) х2 4- 10z-2г / 4-11 = 0-парабола (С = 0). Действительно, х2 + ХОх + 25-2у + 11-25 = 0, (х 4-5) 2 ~ 2у + 14, (ж 4- о) 2 = 2 (у 4-7). Получилось каноническое уравнение параболы с вершиной в точке 0l (-5; -7) ир = 1. 3) 4х2-у2 + 8х ~ 8у-12 = 0 (А-С = -4 <0). Преобразуем уравнение: 4 (х2 + 2rc + 1) — (у2 + 8у + 16) -4 + 16-12 = 0, 4 (х + 1) 2- (у + 4) 2 = 0, (2 (я? + 1) + (у + 4)) — (2 (х + 1) — (у + 4)) = 0, (2x + y + 6) (2x-t / -2) = 0.
Это уравнение определяет две пересекающиеся прямые 2×4-у 4-6 = 0 и 2х-у-2 = 0. Людмила Фирмаль

