Гипербола

Оглавление:

Гипер боле Каноническое гиперболическое уравнение Гипербола — это совокупность всех точек на плоскости, и коэффициент разности расстояний от каждой из них до двух заданных точек в этой плоскости, называемых фокусной точкой, является константой, меньшей расстояния между фокусными точками. Фокусная точка представлена F1 и Fj, расстояние между ними представлено 2c, а модуль разности расстояний от каждой точки гиперболы до фокальной точки представлен 2a.

По определению 2a <2c, то есть a <c. Чтобы вывести гиперболическое уравнение, выберите систему координат Ox так, чтобы точки фокусировки F \ и F2 находились на оси Ox, а начало координат было _ Соответствует центру сегмента F1F2. 0) ИП FzfcO) х Трюк имеет координаты Fi (-c; 0) и F2 (c; 0). М (х, у) Пусть M (x; y) — любая точка на гиперболе. Тогда согласно определению гиперболы | AIF | -MFo | -2a или MFi-MF2 до ± 2a, т. Е. + C) 2 + y2-y / (xc) 2 + y’2 = ± 2a После упрощения, как это сделано, получить каноническое гиперболическое уравнение О) где * 6 * ~ ‘ B2 = c2-o2.

Гипербола — это квадратичная линия. Людмила Фирмаль

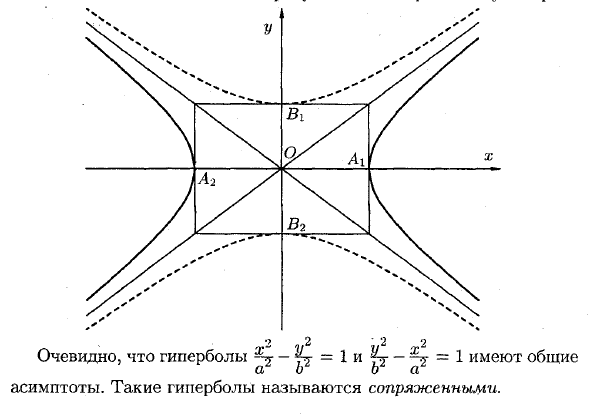
Очевидно, гипербола ^ — ^ r = 1 и C-> ^ = 1 О б Asymptote. Такая гипербола называется сопряженной.Исследование гиперболической формы по уравнениям 1. Уравнение (1) включает в себя х и у только в четных степенях. В результате. Гипербола симметрична относительно осей Ox и Oy и симметрична относительно точки 0 (0; 0), которая называется центром гиперболы. 2. Найти пересечение гиперболы и координатной оси.

Если вы введете y = 0 в уравнении (1), вы найдете два пересечения гиперболы и оси OX. A \ (a; 0) и A-ii-a; 0). Если в (1) введено x = 0,y1 = -b2. В результате гиперболические оси Oy не пересекаются. Точки (a; 0) и A2 (~ a; 0) называются гиперболическими вершинами, отрезок A \ A2 -2a называется действительной осью, а отрезок OAi = OL-2 = a является действительной осью гиперболы. Отрезок B1B2 (£ i £ 2 = 2 &), соединяющий точки B1 (0; b) и B2 (0; -6), называется мнимой осью, а число b называется мнимой осью.

Решение задач по высшей математике

Окружность	Парабола
Эллипс	Общее уравнение линий второго порядка

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Прямоугольник со сторонами 2а и 26 называется гиперболическим основным прямоугольником. 3. Из уравнения (1) приведенный ^ больше или равен 1, т. Е. ^ ^ 1 или | .m | ^ a. Это точка Гипербола находится на правой стороне линии x = a (правая ветвь гиперболы) и на левой стороне линии x = —a (левая ветвь гиперболы). 4. Из гиперболического уравнения (1), когда μ увеличивается, И | у | Это вытекает из того факта, что разность ^ сохраняет постоянное значение, равное 1. ! L \ Y Bi (0; 6) (Γ «y X F \ (-c, Q)) A2 (-a; 0) Ai (a; 0) \ Fi (c \ 0) B2 (0; -6) х = —а х = а Гиперболу можно увидеть, потому что она, как говорят, имеет форму, показанную на рисунке (кривая, состоящая из двух неограниченных ветвей).

Гиперболическая асимптотика Для расстояния d прямая L называется асимптотой неограниченной кривой K. От точки M на кривой K до этой линии, если точка M вдоль кривой K не ограничена, она стремится к нулю.Поскольку прямая (3) и гипербола (1) симметричны относительно координатных осей, достаточно рассмотреть только точки, расположенные в первой четверти указанной линии.

Для расстояния d прямая L называется асимптотой неограниченной кривой K. Людмила Фирмаль

Любовь (а; 0) Возьмем точку N с той же абсциссой x на линии y = -x. Найти разность в точке M (x \ y) на гиперболе y = — \ A2-a2 CL МН между ординатой линии и гиперболической ветвью: MN = -x — y / x2-a2 = ~ (x- \ / x2-a2) = a _ B (x-vr-?) (X + \ [x * -a2) _ 6 a x + Vx2-a2 a x-b \ / x2-a2 Как видите, с увеличением x дробный знаменатель увеличивается. Числитель является постоянным значением. Следовательно, длина сегмента MN стремится к нулю. Поскольку MN больше, чем расстояние d от точки M до прямой линии, d стремится к нулю. Следовательно, строка y- ± -x Oi Гиперболическая асимптота (1). Hyper — аб ‘ х + \ / х2 -а2

Бол (1) Рекомендуется сначала построить главный прямоугольник гиперболы (см. Рисунок) и провести прямую линию через противоположную вершину этого прямоугольника — гиперболическую асимптоту и гиперболические вершины A \ и A-2. вы.Равносторонние гиперболические уравнения с асимптотическими линиями в качестве координатных осей Гипербола (1) называется равносторонней, если ее полуоси равны (a = b).

Ее стандартное уравнение х — у = а. (4) Асимптота равносторонней гиперболы имеет уравнения y = x и y-x и поэтому является биссектрисой координатных углов. Рассмотрим это гиперболическое уравнение в новой системе координат Oh’u ‘, полученной из старой системы координат путем поворота оси координат на угол a = -ZL. Используйте формулу вращения оси. x = x ‘cos a-y’ sin a, y = x ‘sin a + y’ cos a Подставим значения x и y в выражение (4): (“’coe (-J) -y’sm (- ~)) 2- (x’sin (~) + j /’ cos (-J) ) 2 = a2, \ {x ‘+ y’f- ^ (-x’ + y ‘) 2 = a2, x’-y’ = y или y ‘- 2 Где / c = Уравнение равносторонней гиперболы с асимптотикой осей OX и OY имеет вид y = X Другая гиперболическая информация

Гиперболический эксцентриситет (1) представляет собой отношение расстояния между фокусными точками к размеру реальной оси гиперболы. или Когда гипербола c> a, гиперболический эксцентриситет больше 1. e> 1. Эксцентриситет характеризует гиперболическую форму 12 2 LY. Фактически из уравнения (2) ^ =% — 1 (I » n. Ft

Это потому, что чем ниже эксцентриситет гиперболы, Чем меньше отношение, тем больше удлинение, потому что оно является полуосью CL Главный прямоугольник. Эксцентриситет равносторонней гиперболы равен 1/2. конечно _ s _ y / a2 + Q2 _ / 5? a a V a2 Радиус фокуса правой точки ветвления гиперболы e> 1 n = 1 / (x + c) 2 4-y2 и r2 = y / (x к c) 2 + y2, n = ex 4-a и r2 = ежик- Имеет форму а. , А левый-ри- (ежик + а) и г2 = — (экс-а).

Прямая x = ± j называется гиперболической прямой матрицей. с того времени Для гиперболического e> 1, — <a. Это его право Трис находится между центром и правой вершиной гиперболы, а левая находится между центром и левой вершиной. Гиперболические прямые матрицы обладают тем же свойством g = e, что и прямые эллиптические матрицы. Кривая, определяемая уравнением — ^ m-1 B a Вещественная ось 2b находится на оси Oy, а мнимая ось 2a находится на оси Ox. На рисунке это показано пунктирной линией. л / 2.