Оглавление:

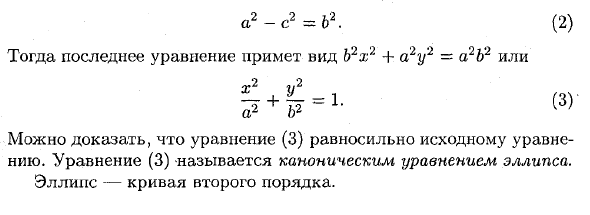




Эллипс
- эллипс Канонические эллиптические уравнения Эллипс — это набор всех точек на плоскости, и сумма расстояния от каждой из них до двух заданных точек на этой плоскости называется фокусной точкой и является постоянной, Чем расстояние между трюками. Фокусная точка выражается как Fi и F%. 2) Расстояние между ними выражается как 2c, а общее расстояние от любой точки эллипса до фокальной точки выражается как 2a. По определению, 2o> 2s, то есть a> s.
Чтобы вывести эллиптическое уравнение, выберите систему координат Oxu так, чтобы точки фокусировки F \ и F-2 находились на оси Ox, а начало координат совпадало с центром отрезка F \ F2. В этом случае трюк имеет следующие координаты: Fi (-c; 0) и F2 (c; 0). Пусть M (x \ y) — любая точка на эллипсе. . (1) На самом деле это эллиптическое уравнение.
Тогда, согласно определению эллипса, MF \ -f MF2 = 2a, то есть yDx + c) 2 4-y2 + y / (x-s) 2 4-y2 = 2a Людмила Фирмаль
Преобразовать уравнение (1) в более простую форму следующим образом: y / (x 4-s) 2 4-y2 = 2a-y / (xs) 2 4-y2, x2 + 2xx + c2 4-Y2 = 4a2-4a • y / (от x до s) 2 4-Y2 4 -x2-2sx + s2 4-y2> ау / (хз) 2 4-? / 2 = a2-еж, a’2zh2-2a2cx 4-a2e2 4-a2? / 2 = a4-2a2szh4-c2®2, (a2-c2) x2 4-a2u2 = a2 (a2-c2). Поскольку a> c, o2-c2> 0. 0) СЗ F2 (с; 0) х
a2-c2 = b2. (2) Тогда последнее уравнение имеет вид b2x2 + a2y’2 = a2b’2 или Мы можем доказать, что уравнение (3) эквивалентно исходному уравнению. Уравнение (3) называется эллиптическим каноническим уравнением. Эллин — это квадратичная кривая.
| Прямая линия на плоскости. Основные задачи | Гипербола |
| Окружность | Парабола |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Изучение формы эллипса по уравнению Установите форму эллипса, используя нормальные уравнения. 1. Уравнение (3) включает в себя x и y только в четных градусах, поэтому, если точка (x; y) принадлежит эллипсу, точка (x; -y), {~ x \ y) y (-x \ -у). Таким образом, эллипс симметричен относительно осей Ox и Oyf, а также симметричен относительно точки 0 (0; 0), называемой центром эллипса. 2.
Найти пересечение эллипса и координатных осей. Если y = Q, вы можете найти две точки A \ (a; 0) и A2 (-a; 0), где ось Ox пересекает эллипс. d.d_a.o) Положите уравнение (3) x = 0 и найдите пересечение эллипса и оси Oy: B \ (0 \ b) и в Bi {Q \ b) О F2J х Любовь (а; 0) B2 (0; -6) (0; -б). Точки A \, A-2, By называются вершинами эллипса. Сегмент A1A2 и его длина 2a и 2b называются соответствующими Большая и малая оси эллипса соответственно. 3. Из уравнения (3) каждый элемент слева t2 Единство, то есть не должно превышать неравенства ^ ^ 1 b2 ‘a u ^ m ^ 1 или -a ^ x ‘^ ak-b ^ y ^ b.
Числа a и b называются большой и малой полуосями эллипса соответственно. Людмила Фирмаль
Таким образом, все точки эллипса находятся внутри прямоугольника, образованного прямыми линиями x = ± a, y ~ ± b. ‘2 и 2 4. Сумма неотрицательных членов ^ и jj в уравнении (3) Равно 1 В результате, когда один член увеличивается, другой член уменьшается. То есть увеличение | .m | уменьшает \ y \ и наоборот. Из вышесказанного эллипс имеет нарисованную форму Рисунок (эллиптическая замкнутая кривая). 3. Другая информация об эллипсе Форма эллипса зависит от отношений. Если b = a, эллипс В виде круга эллиптическое уравнение (3) принимает вид x2 + y2-a2. Отношение — как особенность формы эллипса.
Соотношение половины расстояния между фокусом и будкой (I Полуось эллипса называется эксцентриситетом эллипса и обозначается буквами £ («эпсилон»). (4) и е = но в д f \ r \ r2 \ \ …_ х7 V1оФ-г) x = f X Также, так как 0 <c <a, 0 <e <1. Учитывая уравнение (2), уравнение (4) можно переписать в виде e = — =}. E = y 1- и a = ^^ ~~ e’2 ‘^ Цула видно) Эксцентриситет эллипса и уплощение эллипса уменьшаются. Если e = 0, эллипс является кругом. Пусть M (x; y) — любая точка на эллипсе с фокусными точками F \ и Fo. Длины отрезков F \ M-r \ и F} M = r2 называются фокусным радиусом M. N + r2 = 2а. Формулы держать 7’i = 4-ex и r2 = a-ex Строка x = ± называется эллиптической матрицей.
Значение эллипсоидальной коробки раскрывается утверждением Теорема 1. Если r — расстояние от любой точки эллипса до фокальной точки} d — расстояние от той же точки до прямой матрицы, соответствующей этой фокальной точке}, то отношение ^ является константой, равной эксцентриситету эллипса ^ = е , Из уравнения (2) a> b. Если a <b, уравнение (3) определяет эллипс, главная ось которого равна 2b на оси Oy, а малая ось 2a на оси Ox. Фокус такого эллипса находится в точках F \ (0] c) и jF2 (0; -c). Где с = \ / b2-а

