Оглавление:

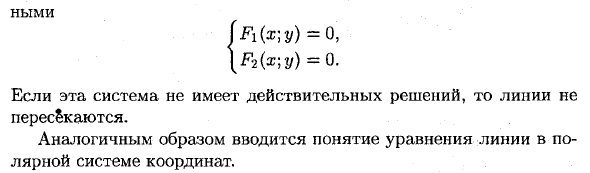


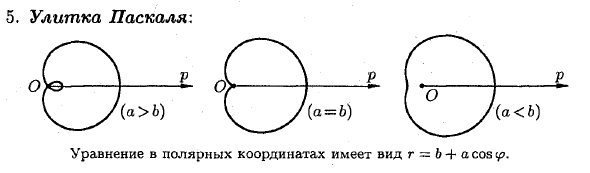
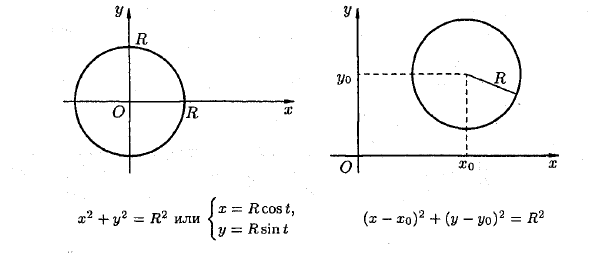
Уравнение линии на плоскости, примеры
- Линейное уравнение на плоскости случай Линии на плоскости рассматриваются (задаются) как набор точек с определенными для них геометрическими свойствами. Например, круг с радиусом R — это набор всех точек на плоскости, которая находится на расстоянии R от некоторой фиксированной точки O (центр круга). С введением системы координат на плоскости заданы два числовых значения (координаты) для определения положения точки на плоскости, а уравнение (т. Е.
Уравнение, связывающее координаты точек линии) используется для определения положения на плоскости. Вы можете определить положение линии. Уравнение для линии (или кривой) на плоскости Оху представляет собой уравнение F (x; y) = 0, которое удовлетворяет координатам x и y каждой точки на линии и не удовлетворяет координатам точек, не находящихся на этой линии , Линейные уравнения можно использовать для замены исследований уравнений путем изучения геометрических свойств линий. Поэтому, чтобы проверить, находится ли точка A (#o; yo) на определенной линии, проверьте, удовлетворяют ли координаты точки A уравнению для этой линии в выбранной системе координат (геометрическая).
Переменные x и y в уравнении линии называются текущими координатами точки линии. Людмила Фирмаль
Достаточно проверить (вне зависимости от конфигурации). Пример: точки K (~ 2; 1) и L (1; 1) на линии 2×4-4 / 4-3 = 0? ♦ Подставляя координаты точки K в уравнение вместо x и y, 2 • (–2) 4-14-3 = 0. Следовательно, точка K находится на этой прямой. Точка L не находится на этой линии. Потому что 2-14143 ^ 0
♦ Задача нахождения пересечения двух прямых, заданного уравнениями F \ (x; y) = 0 и F-2 (x \ y) = 0, находит или решает точку, в которой координаты удовлетворяют обоим уравнениям линии Будет система из двух уравнений с двумя неизвестнымипо \ F2 (x-, y) = 0 Если для этой системы нет действительного решения, линии не будут пересекаться. Аналогичным образом вводится понятие линейных уравнений в полярной системе координат.
| Основные задачи на метод координат (на плоскости) | Различные виды уравнений прямой на плоскости |
| Преобразование системы координат | Прямая линия на плоскости. Основные задачи |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- «Уравнение F (r; <£>) = 0 называется уравнением для конкретной прямой в полярной системе координат, если только координаты точек на этой линии удовлетворяют этому уравнению. Может быть установлен с использованием двух уравнений х = х (т), Y = у (т)> Где xnu — координата произвольной точки M (x \ y) на данной прямой, а t — переменная, называемая параметром. Параметр t определяет положение точки (i; y) на плоскости.
Например, если x = L-1, s / = £ 2, значение параметра t = 2 соответствует точке (3; 4) на плоскости. х = 2 + 1 = 3, у = 22 = 4. Когда параметр t изменяется, точка на плоскости перемещается, чтобы описать указанную линию. Этот способ определения линии называется параметрическим, а уравнение (1) называется параметрическим уравнением линии. Подстановка t = x во второе уравнение облегчает получение уравнения y = x2. Или y-x2 = 0, то есть F (: r; y) = 0. Однако имейте в виду, что такие переходы не всегда рекомендуются и не всегда возможны.
Чтобы перейти от параметрического уравнения линии к уравнению вида F (x \ y) = 0, вам нужна некоторая форма из двух уравнений. {х = т: по Y = т Людмила Фирмаль
Линия на плоскости может быть задана векторным уравнением r = r (t). Где t — параметр скалярной переменной. Каждое значение к является конкретным вектором плоскостей? Соответствует O = r (to). При изменении параметра t конец вектора r = f (t) описывает строку. Два скалярных уравнения соответствуют векторному уравнению прямой r = f (t) в системе координат Оху (1)
Представление линии является ее параметрическим уравнением. Уравнения линейных векторов и параметрические уравнения имеют механическое значение. Когда точка движется на плоскости, указанное уравнение называется уравнением движения, линия называется точечной траекторией, а параметр t является временем. Таким образом, любая прямая на плоскости соответствует уравнению вида F (x \ y) = 0.
Выражение вида F (x; y) = 0 обычно имеет конкретную строку, характеристики которой определяются этим выражением (выражение «в общем случае» допускает исключения) Поэтому выражение (x-2) 2-f (y -H) 2 = 0 соответствует не прямой, а точке (2; 3), уравнению на плоскости x2 + y2 4- 5 = 0 не соответствует ни одному геометрическому изображению). Есть две основные проблемы с аналитической геометрией на плоскости.
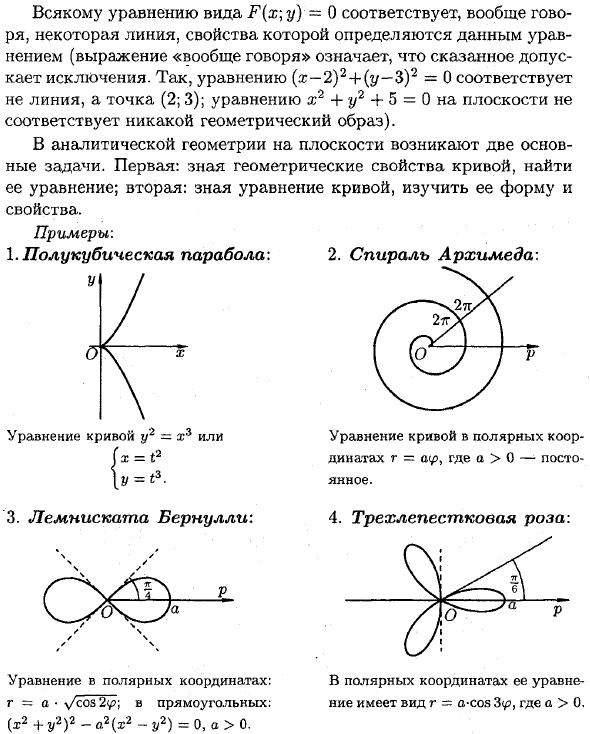
Сначала узнайте геометрические характеристики кривой и найдите ее уравнение. Второе: знать уравнение кривой и изучать ее форму и характеристики. Пример: 1. Полукубическая парабола: 2. Спираль Архимеда: 4. Три лепестка розы: В Y / / — \ 2т / л // 2U \ О V (ч? J / V Уравнение кривой y2 = x3 или уравнение полярной кривой dinates r = r , где a> 0 — константа. 3. Лемнис Ката Бернулли: Уравнение в полярных координатах: уравнение в полярных координатах r = a \ v / cos 2 0. (X2 + y2) 2-a2 (x2-y2) = 0, a> 0.
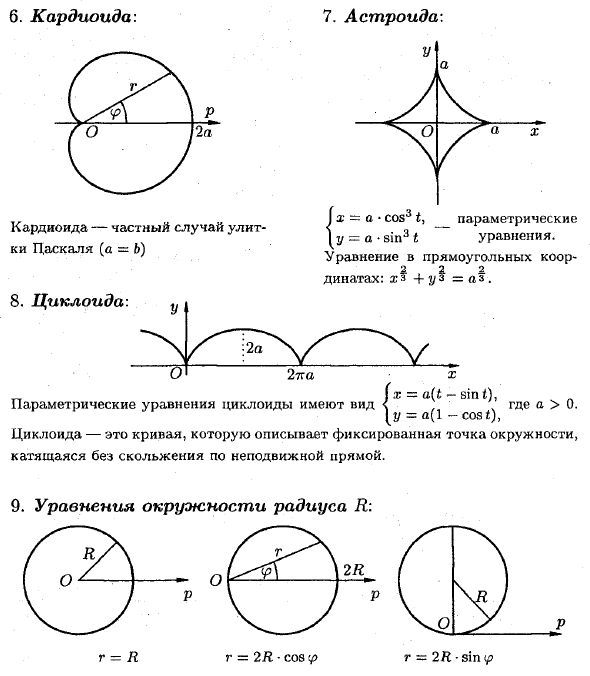
Паскаль Улитка: > B) V J (a = 6) Форма полярного уравнения координат r = B + cos ip.Кардиоидный: 7. Астроид: Кардиоидный улитка Паскаль особый случай (а = б) \ x = a-cos3 _ параметрическое \ y = a • sin3 t уравнение. Декартово координатное уравнение имеет вид zs + uz = «z. 8. Циклоид: _] .t = a (t-sin t), Форма циклоидального параметрического уравнения: <где a> 0. (Y = a (1-her » Стоимость) » Циклоид — это кривая, которая показывает, что неподвижная точка на круге катится без скольжения вдоль фиксированной линии.(Х-хо) 2 + (у-йо) 2 = Н2 x2 + y2 = R2 или <n. ■ = Ксин т

