Оглавление:


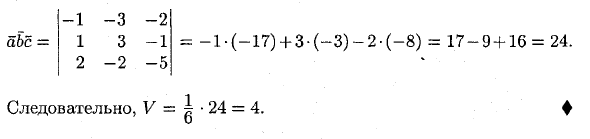
Выражение смешанного произведения через координаты. Применение смешанного произведения
- Представление смешанных работ по настройке. Применение смешанных работ По заданному вектору a = axi + ayj + azk, b = bxi 4-4-bzk, c = c ^ r 4 cyj +, найти их смешанное произведение с помощью выражений координат вектора и скалярного произведения , (Ia x b) c = г 3 ~
- Ах ах ах K от b Z аз-ах b £ i-bx но б Чиж ш. (Cxi 4-Cyj + CZK) — j) • {cxi + cy] + czk) = *, a- О К 1 + в о к О б (1) C „4 • Sz- азбука Это потому, что правая часть уравнения (1) представляет собой разложение кубического определителя на элементы в третьей строке.
Полученное выражение можно записать кратко: о к Cx az bz cz а. Людмила Фирмаль
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Таким образом, смешанное произведение векторов равно кубическому определителю, состоящему из координат умноженных векторов. Некоторые виды использования для операций смешивания 1. Определение взаимной ориентации векторов a, b и c: если abc> 0, a, 6 и c — правые тройки.
Если abc <0, a, 6 и c — тройки слева. 2. Установить компланарность векторов a, 6 и c: а. = O глаз Kuzu B * на bz = 0 <1 = вектор а, Car Su Cz 3. Найдите объем параллелепипеда и треугольной пирамиды.
Построен на векторах a, b и c: объем параллелепипеда: V = \ abc] \ объем треугольной пирамиды: V-g | a £ c |. Людмила Фирмаль
Пример: вершинами пирамиды являются точки A (1; 2; 3), I (0; -1; 1), C (2; 5; 2) и D (3; 0; -2). Найдите объем пирамиды. ♦ найти вектор а. 6, с: a = AB = (-1; -3; -2), 6 = AC = (1; 3; -1), c = AD = (2; -2; -5). Поиск abc:= -1 • (-17) + 3- (~ 3) -2 • (-8) = 17-9 + 16 = 24. -1 -3 -2 1 3 -1 2 -2 -5 abc = Следовательно, V = i • 24 = 4. ♦

