Оглавление:





Краевой эффект в цилиндрической оболочке
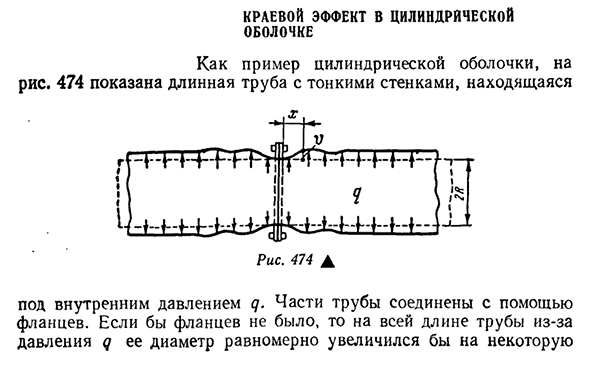
- Влияние края цилиндра Ракушка В качестве примера цилиндрической оболочки она показана на рисунке. 474 показана длинная трубка с удлиненными стенками Под внутренним давлением все части трубы соединяются фланцем. При отсутствии фланца общая длина трубы по диаметру давления d увеличивается равномерно на определенную величину. Рассмотрим жесткость
таким образом, чтобы увеличением диаметра фланца можно было пренебречь, а диаметр трубы фланца оставался неизменным. Но понятно, что от этого произойдет расширение трубы. В результате труба получит в виде рисунка определенную область возле стенки фланца. Этот изгиб стенки (эффект кромки) сначала предполагает отсутствие продольной силы в поперечном сечении трубы.
Средний радиус трубы до деформации/?А толщина стенок-вертикальная Людмила Фирмаль
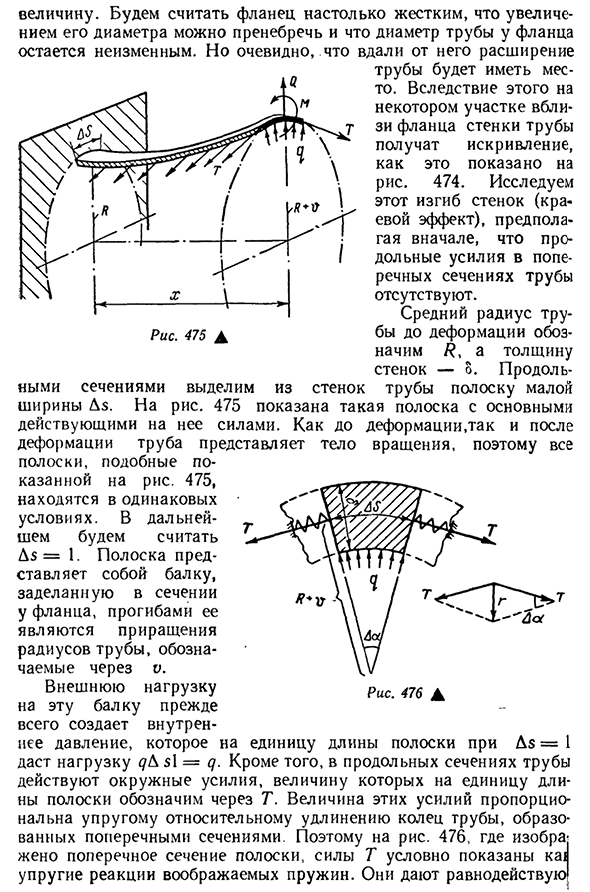
полоса трубы. Я Рис 475А X1- Это показано в 474. Исследовать Выберите из ширины стенок Dz. Для риса. На рис. 475 показана основная сила, действующая на такие полосы. Как до, так и после трансформации трубка представляет собой вращающееся тело, поэтому все полоски расположены так, как показано на рисунке. 475-это то же самое условие. В дальнейшем мы будем рассматривать D z=1. Полоса представляет собой балку, которая герметизируется в поперечном сечении фланца, прогиб которого представляет собой
приращение радиуса трубы, обозначенного V. Внешняя нагрузка этого луча главным образом создает внутреннее давление давая нагрузку DD Z1=<7 в длину блока прокладки DZ=1. Кроме того, в продольном сечении трубы, размер полосы на единицу длины, поскольку размеры этих сил формируются поперечным сечением фигуры. В 476 году, когда было изобретено поперечное сечение полосы, сила Т условно обозначалась как упругая реакция воображаемой пружины. Они дают в итоге 566щую г, которую можно рассматривать как балочную полосовую нагрузку. Из рисунка. 476-г=2T81p — » Т А8 Р2 1I4-в’ Или
- игнорировать размера в сравнении с делителя/? И пусть D z=1, мы получим относительное удлинение радиуса G=4—(19.12), а относительное удлинение стенок трубы в окружном направлении будет соответствующим окружным напряжением по закону крюка. И так оно и есть., уравнение(19.13)показывает, что сила g может рассматриваться как упругая реакция, которая сопротивляется отклонению V полосы балки с коэффициентом пропорциональности Таким образом, дифференциальное уравнение изгиба полосы, изолированной от цилиндрического сосуда, обсуждалось ранее в главе 90, чтобы записать как балку на твердом упругом основании это уравнение принимает вид h-4^= -^ -. (19.14) где значение Y-момент
инерции поперечного сечения полосы, а D8=I= = 83/12. В выражении изгибной жесткости полосы нормальный модуль е не применяется, а вытягивается изгибом за счет взаимодействия с соседними полосами. Форма 567e2 не существует. Например, в случае удлинения волокон а и Е полосового элемента, показанного на фиг. 477, длина сторон AC и JY не изменяется. Принимая уравнение (3.45) закона крюка плоских напряженных состояний§33, с E2=0, в этом случае соотношение между напряжением и расширением SC выглядит следующим образом: В этом случае распределение A2==p, O1 и напряжения изгиба в торцах полосовых элементов показано на рисунке. 477.
Итак, вместо модуля E в данном случае нужно использовать модуль=с учетом этого, и жесткость изгиба полосы E^будет равна: Е г———-Б * Е 1 1 2(1 — / L2) • Согласно значению коэффициента[3§90, он выглядит так (19.15)) В Людмила Фирмаль
поперечном сечении трубы предполагается, что продольные силы действуют и характеризуются равномерно распределенными напряжениями. Относительное удлинение в окружном направлении в этом случае определяется уравнением Отсюда мы представляем a, а затем T: T=o, t=6- / o+n C , И Формула(19.12), 4-го числа Последний член здесь должен добавить знак минус к внешней нагрузке D, учитывая, что удлинение продольной трубы из-за напряжения ZT сопровождается ее сужением. Это, как мы видим, то же самое, что и добавление отрицательного давления.■ Поэтому учитывайте продольные напряжения В Тонны Уравнение изгиба полосы
составляет O1Y4-4p4o=(19.161 Заметим, что 568 уравнений (19.14)и (19.16) справедливы для любой осесимметричной нагрузки.OO значение e*также переходит в бесконечность. Итак, предположим, что C3= = C4=0. Остальные две константы и C2 находятся из условия, что фланец, т. е. x-0,=0 и o=0. Это дает R-LR_ _ I__ _ _ I& Два. — холинэстераза. И В=-(1-У,√Х (81p{ех4-Соз{а)]. (19.18) теперь легко найти изгибающий момент M и боковую силу (} для ширины полосы 5=1 : М=Е^~ 1< * x2 2/3(1-I * 2) е (Соз(а-81p{а); (19.19) е Соз х. р(19.20 )) Графики V и M, построенные по формулам (19.18)и(19.19), показаны на рисунке. 478, где безразмерные координаты откладываются вдоль абсциссы [ex. Для сравнения, значения o, M и 0 в нашем случае представлены функциями и t}2, а в 91, при действии одной концентрации прогиб
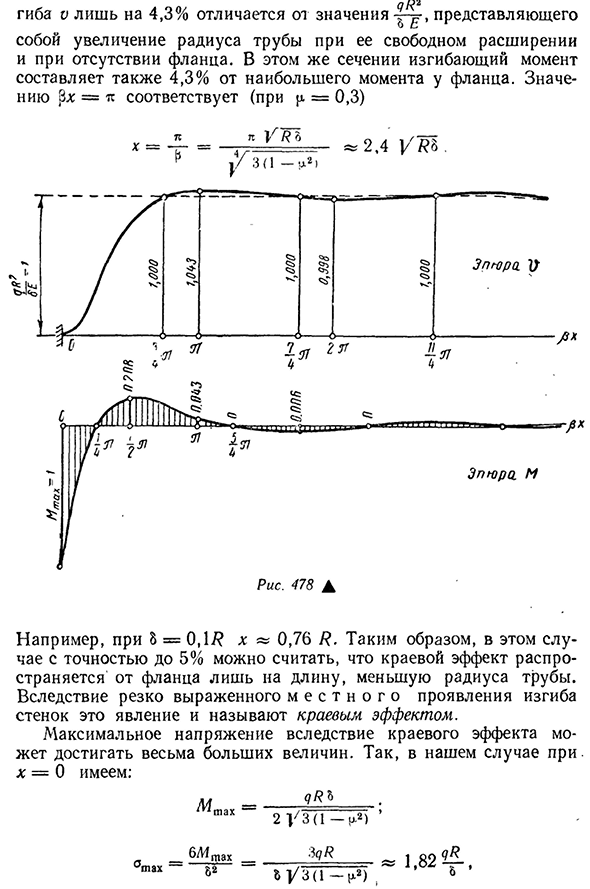
бесконечно длинной балки на упругое основание, момент этого совпадения не случаен. Трудно понять, что наша задача может быть интерпретирована как задача изгиба полосы, отделенной от трубы, как балка на упругом основании под действием сосредоточенной силы, эта сила явно является реакцией фланца. Из рисунка. 478 и функция t из таблицы; и (см. 91) расстояние от фланца и волна деформации изгиба стенки трубы могут быстро затухать. Следовательно, значение At|3x=l Pro- 20З аказ нет.Только 1037 569giba V4, 3% отличается от величины, представляющей собой увеличение радиуса трубы при отсутствии свободного выдвижения и фланцев. В этом же сечении изгибающий момент составляет 4,3% от максимального момента фланца. Значение ZX-TS соответствует(при р=0,3) Например, 8=0,17? х » 0.76 7?. Поэтому в данном случае точность составляет 5%, и можно оценить, что краевой эффект
распространяется от фланца на длину меньшую, чем радиус трубы. Из-за ярко выраженного проявления изгиба стенок это явление называют пограничным эффектом. Максимальное напряжение тока должное к влиянию края может достигнуть очень большие значения. Итак, если x=0, то это выглядит так: М=_ _ _ 2^ — ——— -• т а x2Y з(1 -^)’ Сегодня. 570что(при п. -0,3) в 1,82 раза больше максимального напряжения(19,4), заданного сиюминутной теорией. Если материал оболочки-пластик, например пластиковая сталь, увеличение напряжения из-за краевого эффекта не уменьшит общую прочность контейнера, но уменьшит местную прочность. Например, в случае железобетонных резервуаров эти напряжения могут привести к
образованию трещин, что, в свою очередь, может привести к нарушению герметичности резервуара. В этом случае стресс пограничного эффекта борется с помощью различных конструктивных мер. Одним из них является создание предварительного сжимающего напряжения на стенках железобетонного резервуара. Иногда применяют такую конструкцию, как соединение дна, что позволяет полностью или частично свободно расширять стенки и стенки резервуара. Это драматически уменьшает или исключает давление должное к влиянию края вполне.
Смотрите также:

